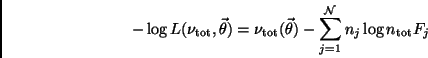Next: Ensemble Tests
Up: tsigex
Previous: Samples
For each sample (i.e. experiment) we fit for the unknown parameters
which are the fraction of events of class 1, 2, and 3. In the ideal situation
the fit should return
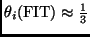 . To perform the fit
we set the fitting PDF to be:
. To perform the fit
we set the fitting PDF to be:
![\begin{displaymath}
F= [\theta_1 P_1 (\vec{x}) + \theta_2 P_2 (\vec{x}) + \theta_3 P_3 (\vec{x})] ,
\end{displaymath}](img72.png) |
(5) |
where the joint PDFs are 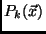 (k=1,2,3). The fitting algorithm
loops over all bins
(k=1,2,3). The fitting algorithm
loops over all bins  and minimized the negative of the log likelihood function:
and minimized the negative of the log likelihood function:
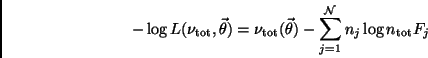 |
(6) |
For each sample we perform three (3) different fits associated with the
different methods used for the calculation of the joint PDF:
- Standard Technique (1D):
The 1D fit is very straightforward and relies on the Eq. (1).
We used 100 bins in the calculation of the joint PDFs.
- Projection and Correlation Approximation (PCA):
The transformed marginal PDFs are mapped into Gaussian.
Although not exact, it represents a good approximation
compared to the standard method when there is
large correlations between the input variables. For each class
one can compute the transformation matrix for
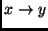 from the MC events. The caveat with the PCA method is
to identify the canonical transformation
from the MC events. The caveat with the PCA method is
to identify the canonical transformation 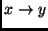 for the data!
The PCA approach works very well
for the calculation of likelihood ratios and was used at LEP
for
for the data!
The PCA approach works very well
for the calculation of likelihood ratios and was used at LEP
for  event selection [2]. It was designed
to classify events as signal (
event selection [2]. It was designed
to classify events as signal (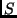 ) or background (
) or background (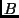 ), where the
signal to background ratio was large (
), where the
signal to background ratio was large (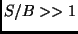 ). At LEP, the data
was therefore transformed like the signal MC. Here, we
have three classes with
). At LEP, the data
was therefore transformed like the signal MC. Here, we
have three classes with
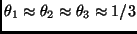 so
there is an ambiguity on how to transform the data; we decided
not to transform the data but to calculate the joint PDFs as described
in Eq. (2).
so
there is an ambiguity on how to transform the data; we decided
not to transform the data but to calculate the joint PDFs as described
in Eq. (2).
- Multi-Dimensional Approach (Multi-D):
The Multi-D fit is also straightforward and relies on the Eq. (3).
Since we have two input variables the fit used a grid of 100
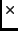 100
bins (i.e. 2D fit).
100
bins (i.e. 2D fit).
The results of each fit is stored and will be used for the ensemble test;
which is described in the next section.



Next: Ensemble Tests
Up: tsigex
Previous: Samples
Alain Bellerive
2006-05-19
![]() . To perform the fit
we set the fitting PDF to be:
. To perform the fit
we set the fitting PDF to be: