


Next: Multi-Dimensional Approach (Multi-D)
Up: Probability Distribution Functions (PDFs)
Previous: Standard Technique (1D)
In the PCA method, a transformation 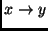 is used [1]. The
monotonic function,
is used [1]. The
monotonic function, 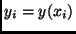 transforms
a variable
transforms
a variable 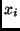 that has a distribution function
that has a distribution function 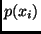 to the
variable
to the
variable 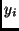 that follows a normal Gaussian distribution
function (of mean 0 and variance 1). Thus
that follows a normal Gaussian distribution
function (of mean 0 and variance 1). Thus
Here 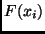 is the cumulative function of
is the cumulative function of 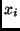 and erf
and erf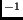 is
the inverse error function. The PCA joint PDF is
is
the inverse error function. The PCA joint PDF is
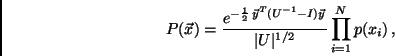 |
(2) |
where 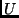 is the covariance matrix for
is the covariance matrix for 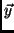 and
and
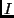 is the identity matrix.
is the identity matrix.
Alain Bellerive
2006-05-19