The samples consist of two random variables and three classes
of events. Each sample can be called an experiment and the goal
is to repeat many experiments to study the statistical analysis
which extract the unknown parameters ![]() . The proposed
toy Monte Carlo is a pedagogical exercise and the objective
is to investigate statistical bias.
. The proposed
toy Monte Carlo is a pedagogical exercise and the objective
is to investigate statistical bias.
The domain for the random variable ![]() is
is ![]() , while the domain for
, while the domain for ![]() is
is ![]() . The analytic or template PDFs used for the three classes are:
. The analytic or template PDFs used for the three classes are:
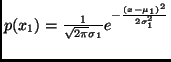 and
and
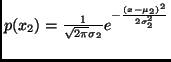 ,
where
,
where 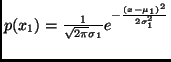 and
and
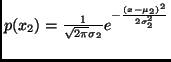 ,
where
,
where
The number of events per class (![]() ) in each experiment are Poisson
distributed with means
) in each experiment are Poisson
distributed with means
![]() . The total number of events
is
. The total number of events
is
![]() . The number of samples generated is
set to 10,000 for the proposed ensemble test study.
. The number of samples generated is
set to 10,000 for the proposed ensemble test study.