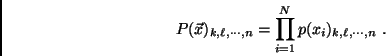Next: Maximum Likelihood Method
Up: Probability Distribution Functions (PDFs)
Previous: Projection and Correlation Approximation
In the multi-dimensional approach, the joint PDF is parametrized bin
by bin. If the correlation is small within each multi-dimensional
bin, the correlation between the input variables can be neglected and the product
of the marginal distributions is a good approximation of the joint PDF.
In the case of a vector of measurements
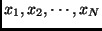 ,
the marginal distributions depend on the bins
,
the marginal distributions depend on the bins
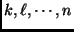 ;
where
;
where 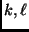 and
and 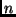 are the bin index associated with
are the bin index associated with 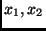 and
and 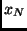 , respectively.
Hence for any value of
, respectively.
Hence for any value of 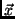 the PDF is given by
the product of Monte Carlo 1-dimensional distribution functions
for the corresponding binned grid
the PDF is given by
the product of Monte Carlo 1-dimensional distribution functions
for the corresponding binned grid
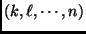 :
:
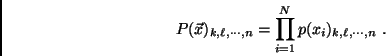 |
(3) |
In practice, one must rely on a finite number of bins so that
the PDFs are defined with enough Monte Carlo statistics. Binning
effects are an inherent limitation of the multi-D method.
Alain Bellerive
2006-05-19