


Next: Samples
Up: tsigex
Previous: Multi-Dimensional Approach (Multi-D)
Consider a set of variables
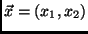 .
The decision to classify an event into one of the three classes
.
The decision to classify an event into one of the three classes
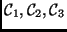 in based on the vector of measurements
in based on the vector of measurements 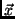 and the joint
PDFs
and the joint
PDFs
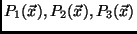 . It is virtually impossible to
decide the event class on an event-by-event basis. Hence we
rely on a statistical analysis of the data to classify which events
belong to
. It is virtually impossible to
decide the event class on an event-by-event basis. Hence we
rely on a statistical analysis of the data to classify which events
belong to
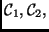 or
or
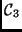 based on the
measured
based on the
measured 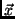 and our best approximation of the associated
joint PDFs
and our best approximation of the associated
joint PDFs
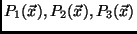 .
.
The random variables 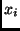 (
(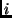 =1,2) for each class are distributed
according to the joint PDF
=1,2) for each class are distributed
according to the joint PDF
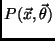 , with unknown parameters
, with unknown parameters
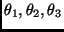 being the fraction of event of class
being the fraction of event of class
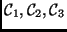 . The extended maximum likelihood
function [3] can be written as
. The extended maximum likelihood
function [3] can be written as
![\begin{displaymath}
\log L (\nu_{\rm {tot}}, \vec{\theta}) = -\nu_{\rm {tot}}(\v...
..._j + \theta_2 P_2 (\vec{x})_j + \theta_3 P_3 (\vec{x})_j] ,
\end{displaymath}](img47.png) |
(4) |
where
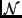 is the number of bins,
is the number of bins, 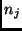 is the number of events in bin
is the number of events in bin 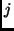 , and
the Poisson distributed variable for the total number of events is
, and
the Poisson distributed variable for the total number of events is
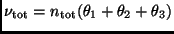 .
.
Alain Bellerive
2006-05-19
![]() (
(![]() =1,2) for each class are distributed
according to the joint PDF
=1,2) for each class are distributed
according to the joint PDF
![]() , with unknown parameters
, with unknown parameters
![]() being the fraction of event of class
being the fraction of event of class
![]() . The extended maximum likelihood
function [3] can be written as
. The extended maximum likelihood
function [3] can be written as