

|
Easiest to visualize are water waves , but also
Waves in slinky
Waves in string
Sound waves
Light Waves
Guitar/violin string
Drum head
If wave travels a distance δx in δt = t₂-t₁ then v = δx/δt |
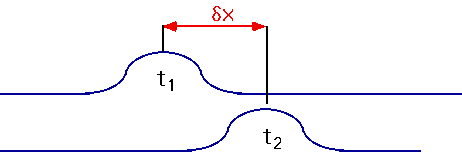 |
| Because it is mathematically simple, we will often use harmonic waves: i.e. sine waves: As before v is speed at which one crest (or trough) moves | 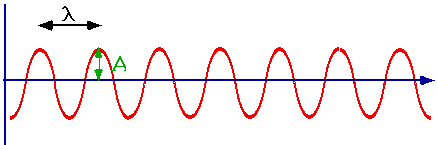
|
Speed = wavelength x frequency
v = λf
(why?)
| e.g. Slinky | 
|
| Molecules move backwards and forwards to create regions of higher or lower density. Note sound travels through a solid in exactly the same way |  |
| Tranverse waves can be polarized in the vertical plane, or the horizontal plane or anywhere in between | 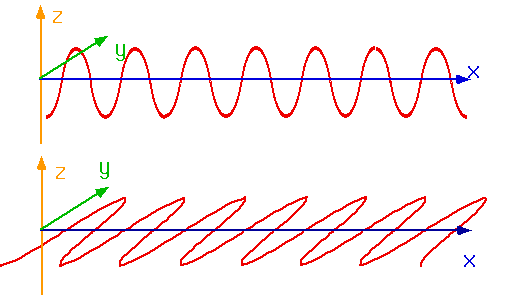
|
What governs the speed of a wave?
v = (T/ρA) 1/2
f = v/λ(write it this way since λ is defined by "shape" of object and v by mech. props)
|
 |
| Nodes are points were string does not move: points half way between with maximum motion are antinodes. | 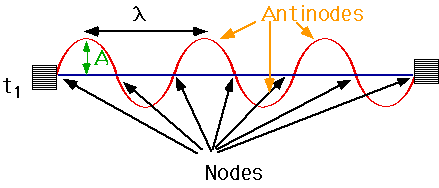 |
| Most wind instruments have one open end e.g. flute, oboe, beer-bottle, organ... | 
|
Note what is really happening is that the molecules move a lot at the antinodes but are stationary at the nodes.In particular,there is no motion at the closed end. The fundamental in this case has 1/4 wave λ = 4 L λ = 4L/3This is 3/4 wave. |
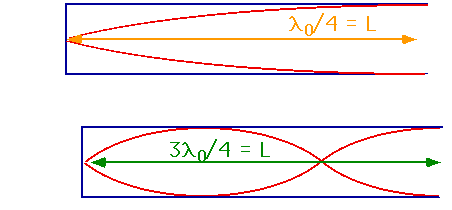
|
λ = 4 L/(2n+1)
f = (2n+1) v/(4L)Note harmonics are not one octave higher.
| C | 8.2 | 16.4 | 32.7 | 65.4 | 130.8 | 261.6 | 523.3 | 1046.5 | 2093.0 | 4186.0 | 8372.0 |
| Db | 8.7 | 17.3 | 34.6 | 69.3 | 138.6 | 277.2 | 554.4 | 1108.7 | 2217.5 | 4434.9 | 8869.8 |
| D | 9.2 | 18.4 | 36.7 | 73.4 | 146.8 | 293.7 | 587.3 | 1174.7 | 2349.3 | 4698.6 | 9397.3 |
| Eb | 9.7 | 19.4 | 38.9 | 77.8 | 155.6 | 311.1 | 622.3 | 1244.5 | 2489.0 | 4978.0 | 9956.1 |
| E | 10.3 | 20.6 | 41.2 | 82.4 | 164.8 | 329.6 | 659.3 | 1318.5 | 2637.0 | 5274.0 | 10548.1 |
| F | 10.9 | 21.8 | 43.7 | 87.3 | 174.6 | 349.2 | 698.5 | 1396.9 | 2793.8 | 5587.7 | 11175.3 |
| Gb | 11.6 | 23.1 | 46.2 | 92.5 | 185.0 | 370.0 | 740.0 | 1480.0 | 2960.0 | 5919.9 | 11839.8 |
| G | 12.2 | 24.5 | 49.0 | 98.0 | 196.0 | 392.0 | 784.0 | 1568.0 | 3136.0 | 6271.9 | 12543.9 |
| Ab | 13.0 | 26.0 | 51.9 | 103.8 | 207.7 | 415.3 | 830.6 | 1661.2 | 3322.4 | 6644.9 | 13289.8 |
| A | 13.8 | 27.5 | 55.0 | 110.0 | 220.0 | 440.0 | 880.0 | 1760.0 | 3520.0 | 7040.0 | 14080.0 |
| Bb | 14.6 | 29.1 | 58.3 | 116.5 | 233.1 | 466.2 | 932.3 | 1864.7 | 3729.3 | 7458.6 | 14917.2 |
| B | 15.4 | 30.9 | 61.7 | 123.5 | 246.9 | 493.9 | 987.8 | 1975.5 | 3951.1 | 7902.1 | 15804.3 |
| Violin (bowed) | 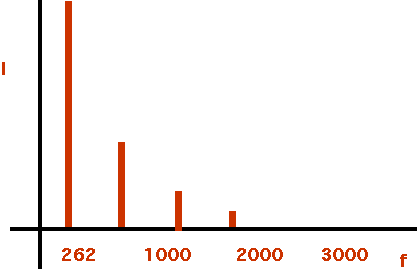 |
| Clarinet | 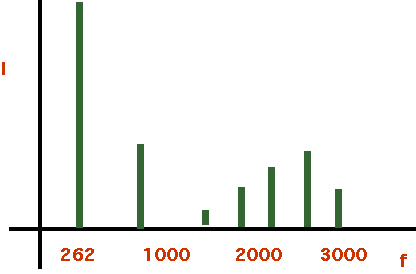 |
| e.g. suppose a guitar string is plucked at the 1/4 distance point. | 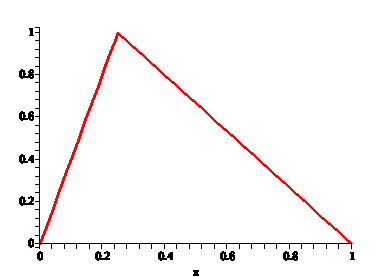 |
| This will excite a fundamental and a set of harmonics. This shows the actual harmonics: note the fundamental is the largest | 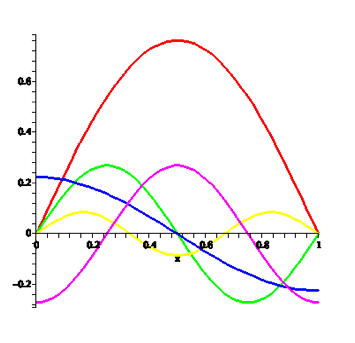 |
| Not obvious that this gives us the original string shape, but we can add in successive harmonics to produce the original shape | 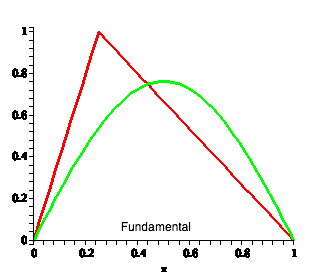
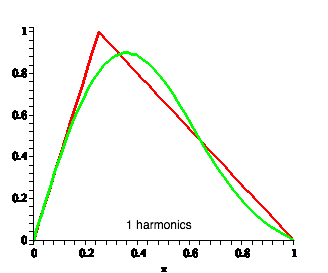
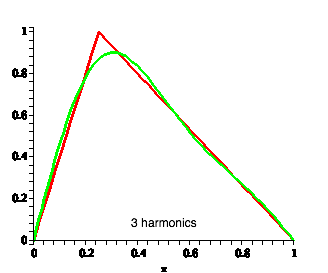
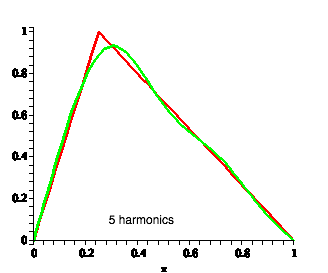
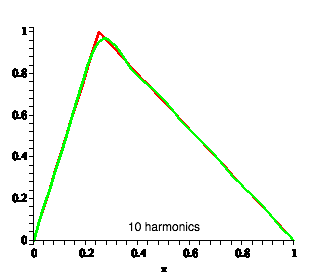
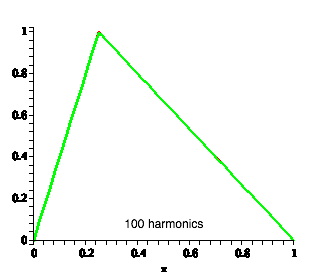
|
| Means we can look at different shapes and find the harmonic content | 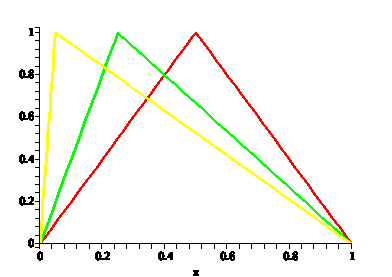 |
| Note that the simplest wave (plucked at half-way) has most fundamental, plucked at .05 gives us largest high harmonics | 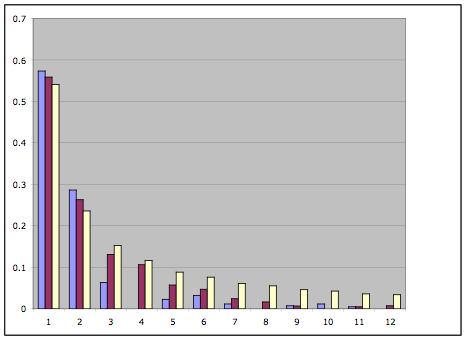 |
| e.g. Shephard scale |
| e.g. Rissett scale |
| Note how the string moves: Not only does the wave move forward, but each individual particle is displaced. This means a wave carries energy. Each particle would have P.E. = 1/2 k x ² where x is the maximum displacement. Also K.E. = 1/2 m v ² so more rapidly oscillating string means larger velocity so... |

|
∝square of frequency
P∝ ω ²|A|²
β = 10 log(I/I0)
| Note that our hearing response is not uniform at all frequencies: Top curve is threshold of pain, bottom is threshold of hearing | 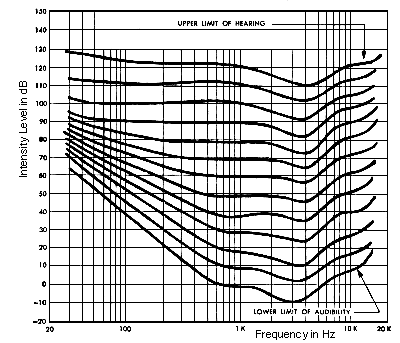 . . |
| Light is part of the whole electromagnetic spectrum | 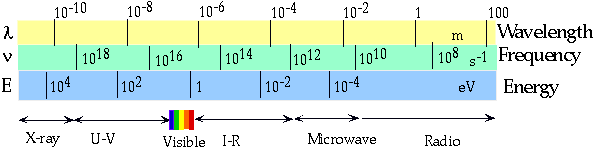 |
c = λf
repeatedly. The "energy' in the above diagram gets explained later. We "see" only one octave.
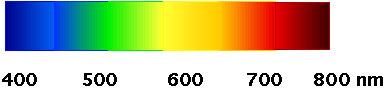
| Why do we see so little of the spectrum? Answer lies in the transparency of the atmosphere | 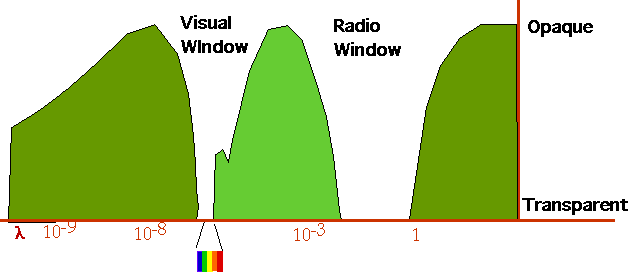 |
| e.g pulses: Waves will pass through each other with no (permanent) effect on each other.
Total displacement will consist of sum of individual displacements e.g. collision of two pulses |
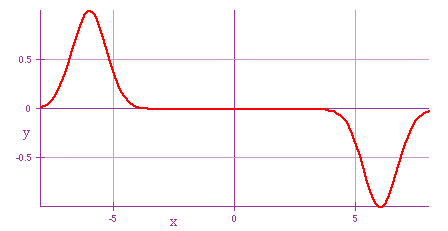
|
| We are usually more concerned about interference between harmonic waves
See how two sin waves add |
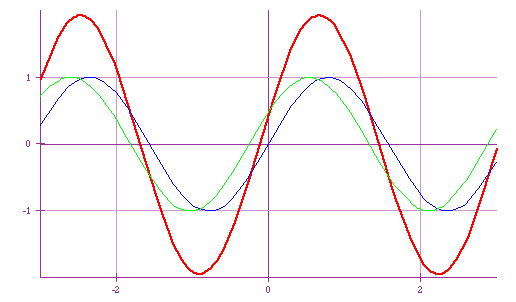 |
| If k₁ and k₂ are different, then they will add up constructively at times and destructively at others. The result is a wave that is sometimes large and sometimes vanishes. See the animation. If this is a sound wave, we hear it as "beats". | 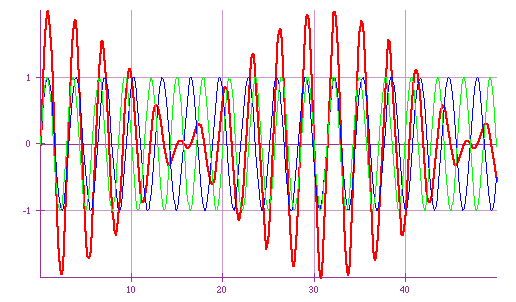 |
Easiest to see with a pulse.
Wave exerts upward force on support => downward force on rope => inversion of original wave |
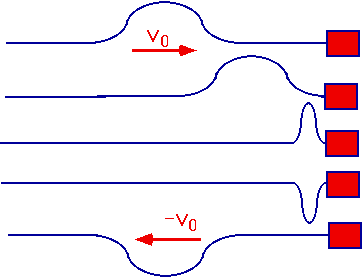 |
|
 |
Wave is partially reflected and partially transmitted Try the animation
| Note: "refracted" wave propagates at a different speed. | 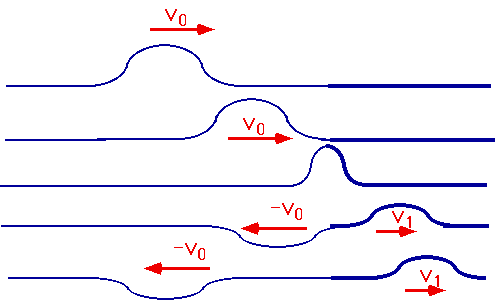 |
| What happens when a light wave hits glass?
Some is always reflected |

|
|
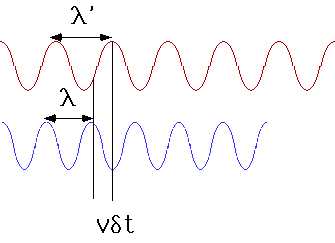 |
Although it may sound silly, we are going to need a way to distinguish waves from particles.
| To simplify the pictures, we will show only the crests of waves (the wavefronts). Note the velocity is perp to the wavefronts | 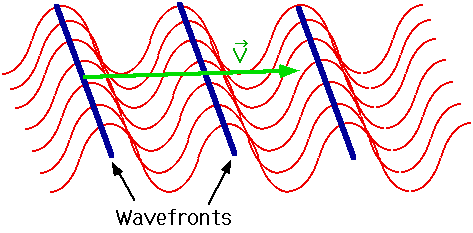 |
| A point source of waves produces spherical waves. If we see them a long distance from the source, they look like plane waves. |  |
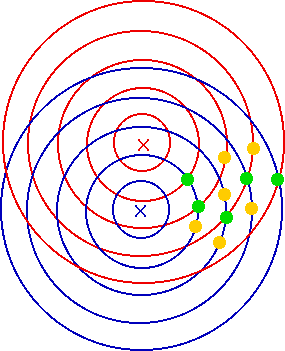
| When we have two sources, we can get interference between them | 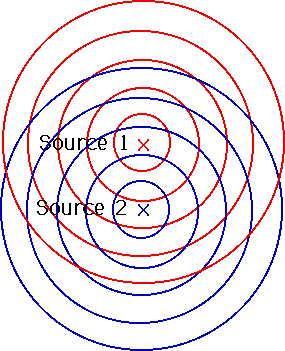 |
| At the green points, we will get constructive interference (crests add)
At the yellow points, we get destructive interference (crest and trough) |
 |
| This means we get nodal lines: (this shows the lines of maxima) | 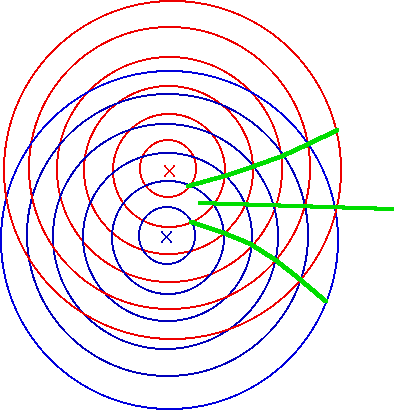 |
| Distance between sources is small (d) Distance to detector is large (D) so waves can be treated as plane waves, giving constructive intereference | 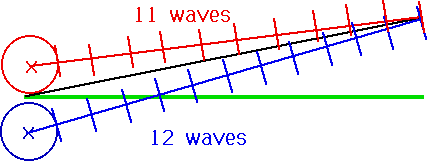 |
| If we have an extra 1/2 λ, will get destructive interference. | 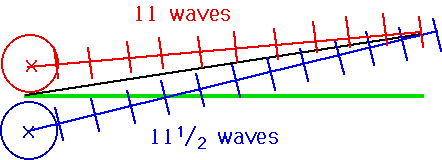
|
| What is the geometry of this?
Must have D1 - D2 = nλ for constructive interference n = 0,±1,±2,±3..................... |
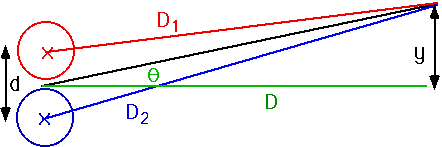 |
θ = nλ
d
| For light, there is an extra problem: sources don't stay in phase... | 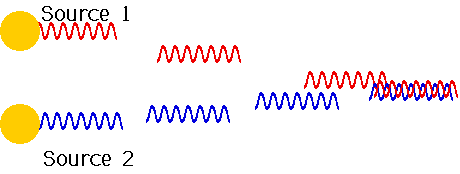 |
| We can overcome this by using the same wave twice! Make two bits of the wave go through separate slits | 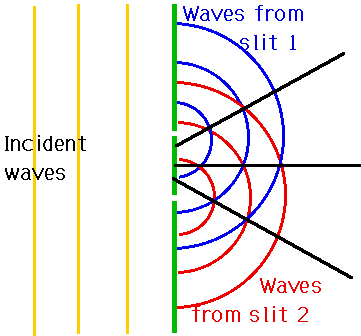 |
| e.g. a light produces Na light (λ = 589 nm) and it passes through two slits separated by 5μ (5x10-6 m). How will it appear on a screen at a distance of 1 m? (more or less 3rd expt) | 
|
A final consequence of General relativity
|
 |
Hence (well, more or less hence!) it requires a large amount of mass to produce a grav. wave, and a large amount to see one: e.g need to detect motions of << atomic radius in a one ton sapphire crystal.
This consists of two neutron stars, in orbit 106 km in radius, with period of hours. Change in frequency allows orbit to be calculated exactly, and can measure..
Rate of precession = 4.22662 0/yr (i.e. 30,000x that of Mercury)
and that pulsar is losing energy, by gravitational radiation (mass~1.4 M0, and accns are large)
| Decrease of the orbital period P (about 7h 45 min) of the binary pulsar PSR B1913+16, measured by the successive shifts T(t) of the crossing times at periastron; the continuous curve corresponds to $$ \color{red}{ T(t) = \frac{{t^2 }}{{2P}}\frac{{dP}}{{dt}}} $$ given by the general relativity (reaction to the gravitational waves emission) | 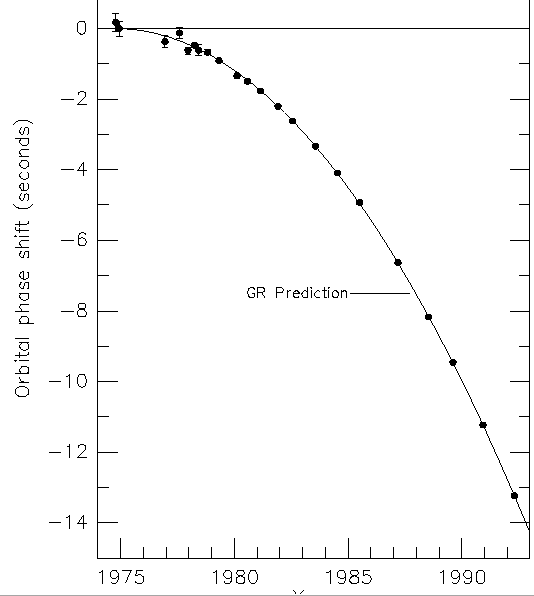 Reference: Taylor J.H. 1993, Testing relativistic gravity with binary and millisecond pulsars, in General Relativity and Gravitation 1992, eds. R.J. Gleiser, C.N. Kozameh, O.M. Moreschi. Institute of Physics Publishing (Bristol). |
Hence 1993 Nobel Prize