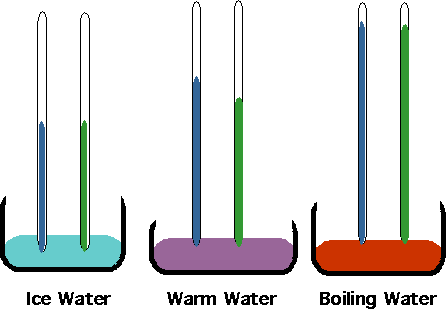
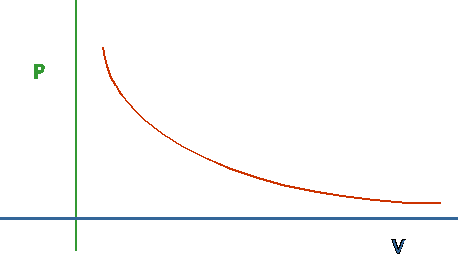
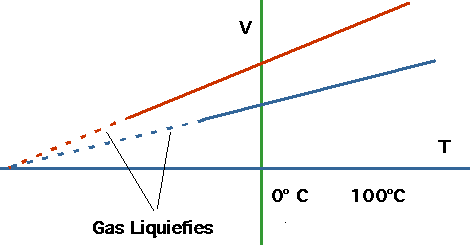
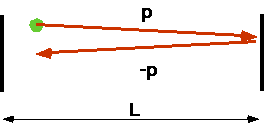
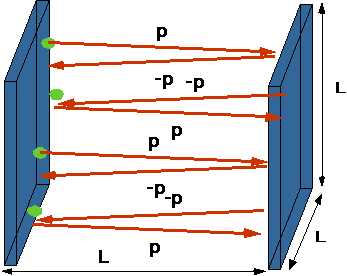
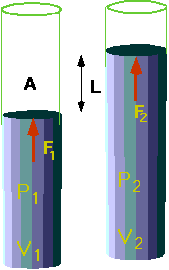
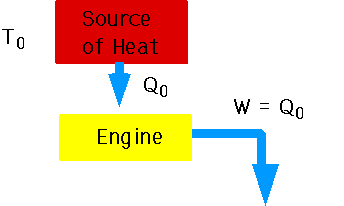
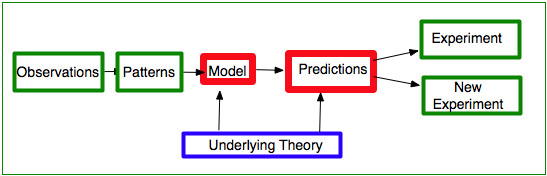
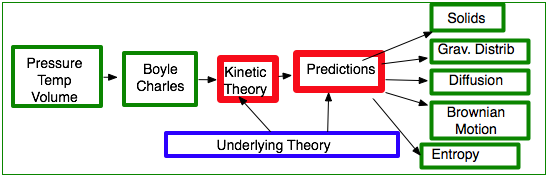
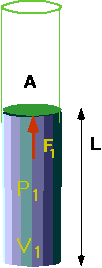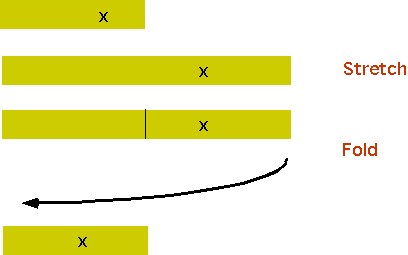Warning: jsMath requires JavaScript to process the mathematics on this page.
If your browser supports JavaScript, be sure it is enabled.

4100 Thermodynamics

Maxwell and Boltzmann

What is heat?

Newtonian Dynamics leads to a predictable (deterministic) system. Are all systems predictable?

Yes and no!
Temperature can be felt qualitatively, but physiological estimates are notoriously bad.
Start by defining fixed points:
- 0°C is water with ice floating in it
- 100°C is boiling water

Even using thermometers, there is no guarantee that two thermometers will measure the same value:
i.e. what is temperature?
Will see this gets an answer from our model for an ideal gas.

First idea was "Caloric": a fluid which flows from a hot body to a cold body, which is created by fire.
e.g. Mix 10 g of water at 100 C with 30 g at 20 C: what is the final temperature?
However: heat and energy are related.
Cannons are made by taking a lump of steel and boring out a hole: generates heat, and apparatus has to be kept cool by water. Count Rumford (Director of Artillery for the Prussian army) noticed that more heat was generated by a blunt bit, and the heat didn't depend on the amount of material removed.
James Watt invented the steam engine, which converts heat into mechanical work. Hence:
heat ⇔ mechanical energy
Both are aspects of energy: hence we will use the unit Joule.
A leftover is the calorie: amount of heat required to raise 1 g of water 1 C. (Note: 1 Cal = 1 kcal = 1000 cals: this is what you eat!)
I calorie = 4.126 J.

There are two views of heat:

"Macroscopic" view of heat: i.e. what quantities can we measure in a lab.
"Microscopic" view: i.e. what happens on the level of atoms and molecules.

The first understanding of this comes from looking at gases.

Heat and the Ideal Gas

So where is the energy in heat? Critical experiments were done with gases:

First consider a gas in a cylinder, kept in place by a piston that can move up and down.Obviously Volume is

V = LA
Pressure: gas applies a force to the piston

P = F/A
Can vary pressure on gas by (e.g.) applying weights to the piston. Measure P in Atmospheres, or Pascals
Nm^-2 = Pascal
1 atm = 1.013 x10⁵ Pa

Boyle found that if the pressure was varied while temp was kept constant.
PV = const.
Charles found that if the temperature was changed at constant pressure:
V = const(T-T₀)

Could only study a small part of the temperature range but found that all gases had the same T₀
```
T₀ = -273°C
```
In practice, the gas will liquefy (e.g. N₂ at ~-200°C) or solidify (e.g. CO₂ at -40°C), and the relation no longer works.
Obviously simpler if we redefine our temperature scale so that T₀ = 0. This defines absolute temp. scale or Kelvin scale: 0 K = -273.16 C
Then
```
V = const T.
```
We can combine Charle's law and Boyle's Law to give "Ideal Gas Law"
```
PV = (constant)T 
```
The constant depends on the number of molecules present.

Kinetic Theory

We will look at a model first: a gas of a few atoms.

The atoms interact only as hard spheres with a rigid wall, all collisions are totally elastic.Collisions with the wall will produce a force on the wall, which is the pressure of the gas. Note that collisions increase as the molecules move faster.
Start with one atom in 1-D!

Newton's 2nd law:
```
F δt = δp
```
Gives average force
```
 F = mv²/L
```
If we have heavy molecules or fast molecules, force will increase

Now suppose we have N molecules present.

Pressure
```
P = F = Nmv²
    A    L²L
```

but volume V = L³ so

PV = N m v² ~ N (kinetic energy of a single molecule)

and previously we had
```
PV = (constant)T 
```
i.e. temperature is nothing but K.E.!.
When we go to 3-D, we get

Average K.E. of molecule = ¹/₂mv² = ³/₂ k_BT

Stefan-Boltzmann constant k_B is (yet another!) constant of nature: it relates Temperature, which is a macroscopic quantity to the average K.E. of a molecule
```
 k_B=1.38x10^-23JK^-1
```
Then we get the proper way to write the ideal gas equation
```
PV = ³/₂ Nk_BT
```

Note that the energy U=¹/₂mv² is the same for all gases. This says that the heavier the molecules of the gas, the slower they move
```
v ~ 1/m^1/2 
```
Is this reasonable?

We can understand a number of things from the kinetic theory: e.g. how an expanding gas can do work, and this leads to .....

The First Law of Thermodynamics

When a gas expands, its energy can change, and it can change the enrgy of its surroundings

Change in internal energy of a system =Heat input - work done
If the piston is allowed to move,then the gas will do work: difficulty is that pressure changes as we go along
e.g suppose we paddle a canoe: mechanical energy in the paddle becomes motion in the water becomes motion of the individual molecules becomes heat
e.g suppose we burn gasoline in a car: the heat energy in the hot gases become mechanical energy transmitted to the tires becomes mechanical energy (and the gas gets cold)
e.g suppose you eat food before running: the food energy is stored in ATP in your muscles, and becomes kinetic energy when you run
This is pretty obvious: it's essentially conservation of energy

Second Law of Thermodynamics

For example, why can't we have (e.g) a boat that takes in water at 20°C, extracts some heat, turns it into energy and exhausts cold water

Doesn't violate first law

In symbolic terms, why can't we have
Shares for investment in the company will be available after the class.

Second Law of Thermodynamics

A man who is ignorant of the second law of thermodynamics can no more claim to be educated than a scientist who has never read Shakespeare or Milton (C. P. Snow, paraphrased)

In order to get work out of a system, one must have a very asymmetrical system
e.g. High pressure one side of a piston, low pressure the other side. Can this arise by chance?
e.g. high temp. one side of a piston Can this arise by chance?
Given 6 atoms, what is probability of finding them all one side of a room? Can model this via coin tossing

Entropy

Essentially the relative probability of finding a particular arrangement by chance. If arrangement is improbable, we can always get work out of it.

Watch the simulation!

Hot gas + cold gas <--> warm gas
Gas molecules will randomize themselves very fast
Microscopic Version of Second Law
a system will always tend towards the most random arrangement

Low entropy Macintosh!
High Entropy Macintosh!
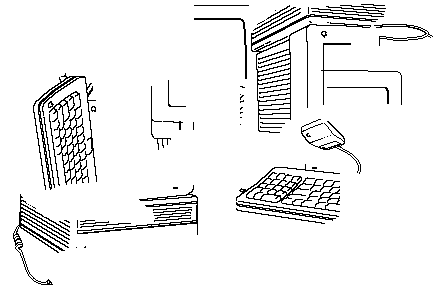It is very probable that dropping a Mac will rearrange it in a more randomly ordered form!
Dropping it again (once or one million times) is not likely to get it working again!

Another version of the 2nd Law:

Entropy tends to increase in a closed system.

Of course we can decrease entropy locally:
How about a fridge? Initially room & fridge at same temp., afterwards T₀ < T₁
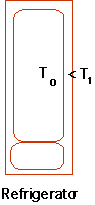Fridge is not a closed system: must include power station. How about hydro-power?

Where does the hydro power come from?

Degradation of energy: high temp. energy in sun <--> low temp. energy here
Note that the nomenclature complicates things unnecessarily: it would be easier if heat was called energy (or maybe heat energy) and entropy was called heat. Then paraphrase of 2nd Law would be
All forms of energy get converted into heat energy. Once all the heat is at the same temperature, can get no further work.

Murphy's versions of the laws of thermodynamics

1st: You can't win
2nd: You can't break even
3rd: You can't quit the game
No, don't put them on an exam!

2nd law and evolution

2nd law has profound philosophical consequences: e.g:
Clearly complexity of animals has increased over history of earth. We are more ordered than amoebas (no moral judgments here!)
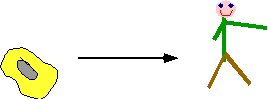Therefore evolution contradicts 2nd law?
Not a closed system!

The connection with time..how is tomorrow different from yesterday?

Or better, how do you know if a movie film is being run backwards?
The "arrow of time" is defined via an increase in entropy.

What happens in the end? i.e how does the universe evolve, assuming that it is expands for ever?
All processes increase entropy, hence end of universe will come when entropy becomes a maximum
When temperature of everything is the same, then can do no work, hence .....nothing! Heat Death of the Universe
"This is the way Worlds end, not with a Bang, but a Whimper" T.S. Eliot

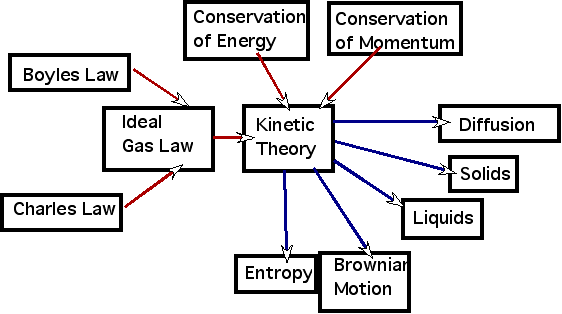
Kinetic theory

provides the understanding for a large number of phenomena:

Boyles/Charles/Ideal Gas law
Entropy & 2nd law
Diffusion: why should you stir your coffee to spread the sugar around?
Conductivity of metals. Can treat the electrons as a gas colliding with the lattice atoms.

Liquids, solids and gases: need to extend model to have forces which are attractive at long range

Gravitational Variations in pressure: why is air pressure on a mountain top lower than at sea level and the temperature is lower?

Brownian Motion: why do grains of pollen vibrate in air?

At micro level

Since the kinetic theory is "obvious" it must have been discovered very early? Almost all scientists associate it with James Clerk Maxwell, who developed it around 1860.

John Herapath and John Waterston both developed the basic structure well before Maxwell. Herapath (1836) assumed that T ∝ vel. of molecules rather than v², so that results were wrong in detail. However speed of sound of a gas, is correct. His actual interests lay in railway engineering, which led to an attempt to calculate the effects of the friction of the air on trains. This had been totally ignored by the engineers of the time: how could something as insubstantial as air possibly have any effect on something as massive as a railway engine? He successfully calculated the force of air resistance, and concluded that
" the idea that trains could operate at 60 m.p.h. or more (as suggested by Stephenson) is absurd;second, every effort should be made to minimize air resistance."
(remember, he was writing in 1836, a mere twenty years after the invention of the steam engine); As part of this, he was able to calculate how fast the molecules were moving, and how far they traveled between collisions.

Result: work rejected by the Royal Society of England
Waterston (1845), avoided the technical mistakes that Herapath made. He was absolutely correct in every important way. The referee’s report reads:
To the Secretary of the Physics Committee, R.S.
Dear Sir,
I have received a paper, from the clouds for ought I know, but I conjecture that it may have been sent to me by Mr. Weld for a report.In my opinion the paper is nothing but nonsense, unfit even for reading before the Society.
I am, dear sir
Yours very sincerely
Lubbock
(Lubbock was an eminent mathematician). The Royal Society refused to return the paper to Waterston so he had no copy. It was rediscovered by Lord Rayleigh, and to some extent publicised by Rayleigh and later by J. B. Haldane. Waterston’s nephew wrote that

"We could never understand the way in which he talked of the learned societies, but any mention of them brought out considerable abuse without any definite reason being assigned."

Heat in summary:

Looks like a disconnected series of phenomena but can understand it in terms of kinetic model Most fundamental principles

First law

, which is (almost) conservation of energy

  δU = Q-W

Second law:

Entropy increases in a closed system

Note what we have done in all this discussion: we have taken

Newton's laws of motion
Conservation of Momentum
Conservation of Energy
and a model for what a gas is.

In terms of our scientific model

Chaotic Motion

She comes, she comes, the sable throne behold
Of Night Primeval and of Chaos old!
...
Physic of Metaphysic begs defence
and Metaphysic calls for aid on Sense
See Mystery to Mathematics fly
In vain! they gaze, turn giddy, rave and die ....
Lo! thy Dread Empire, Chaos is restored
Light dies before thy uncreating Word.
Alexander Pope, The Dunciad

Up to know we have discussed two kinds of system:

Deterministic: i.e. systems whose future can be predicted exactly e.g. planetary system, mass on a spring, pendulum.
Random systems: i.e. ones which are too complex to predict exactly e.g. gas, society...Best we can do is to predict average values
However there are two other kinds of systems:
Chaotic: i.e. systems which are predictable over the short term but not over the long term.
Quantum: systems which are intrinsically unpredictable except in a special sense.

Chaotic systems:

the easiest one to visualize, although technically it is not chaotic, is the "baker transform" The formula is

x_n =2x_n-1 if 2x_n-1 < 1
x_n =2x_n-1 -1 if 2x_n-1 > 1

For example, we can start with two points very close together and see what happens:

Step	Particle 1	Particle 2	Distance
1	0.001	0.0011	0.0001
2	0.002	0.0022	0.0002
3	0.004	0.0044	0.0004
4	0.008	0.0088	0.0008
5	0.016	0.0176	0.0016
6	0.032	0.0352	0.0032
7	0.064	0.0704	0.0064
8	0.128	0.1408	0.0128
9	0.256	0.2816	0.0256
10	0.512	0.5632	0.0512
11	0.024	0.1264	0.1024

If you plot the , it looks nice and smooth to start with, but suddenly looks random.

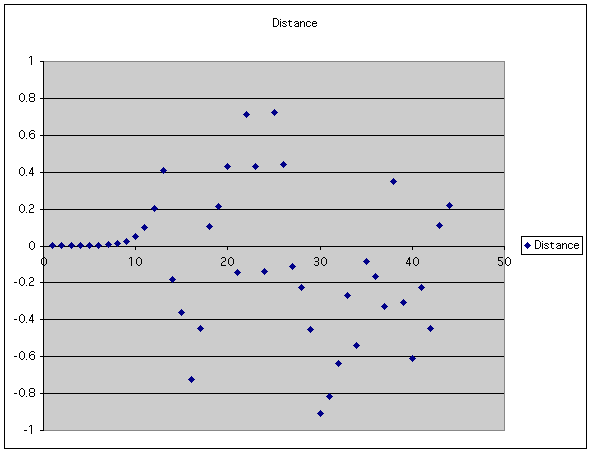The real physics applications relate to the Lorenz equation and similar. The easiest to visualize is the "logistic map", which originally arose in modelling population growth. All chaotic systems have some common features

The equations must all be non-linear
There are regions of the parameters where the motion is predictable
There are regions where it is chaotic
In the chaotic region, points that start off close together become wildly different as time goes on.

Dynamic Map:

Suppose we have a population which grows No. of births ∝ No of live individuals
```
x_birth = k x
```
No. of deaths ∝ no. of live individual
```
x_death = k'x
```
So total number in next generation is
```
x_n = (1+k-k')x_n-1
```
If this is all, population grows exponentially.

However, if the population grows too large, there will be starvation, and this ∝ square of the pop.
```
x_starve = k''x²
```
So total number in next generation is
```
x_n = (1+k-k')x_n-1-k''x_n-1²
```
We can make this look a bit cleaner by writing
```
x_n =r x_n-1(1-x_n-1)
```
" Obviously " what will happen is that the population will grow until the population reaches an equilibrium value? Deaths = Births

This is what happens for r = 2 (say)

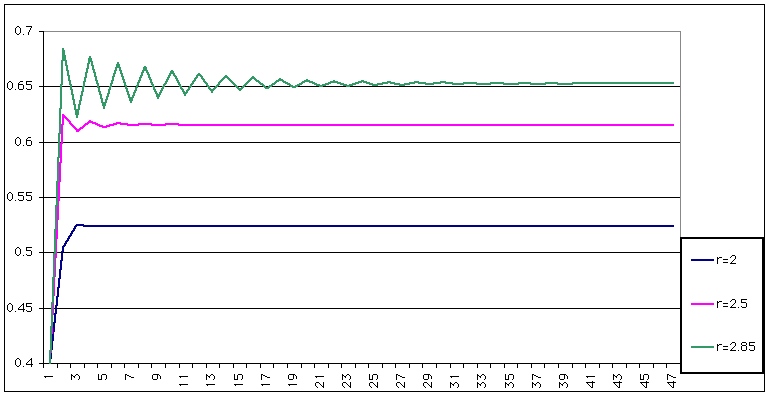However, for r = , a curious effect arises: the number actually oscillates.

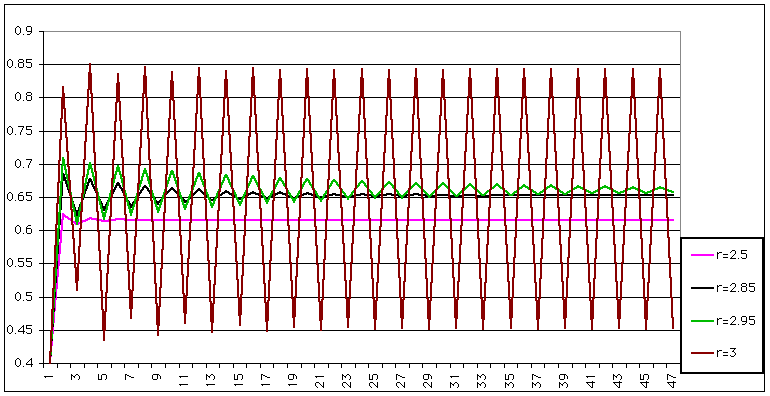This doesn't seem too bad, until you increase r a bit more

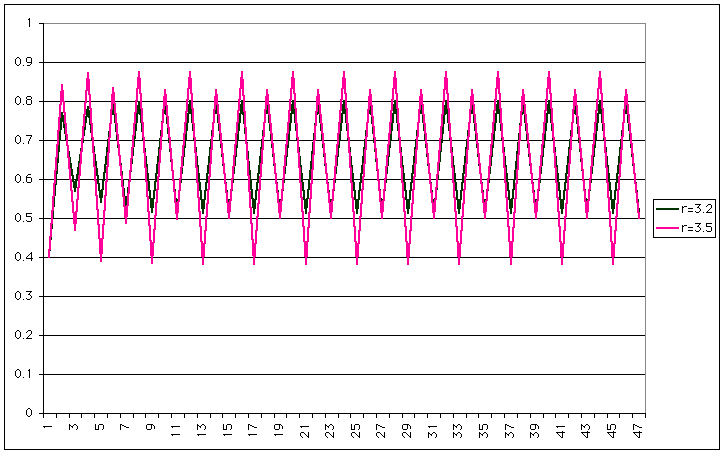Now you have a period 4 (same period, but two different heights). If we increase r a little more, the behaviour becomes chaotic

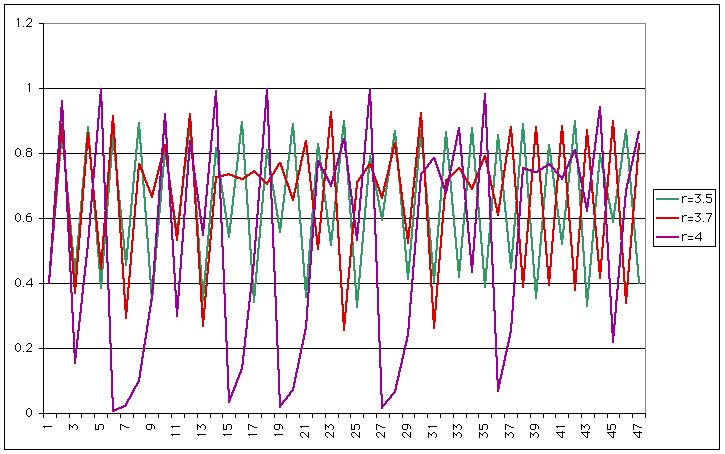There is a nice way of seeing this: a "logistic map." (1Dmap) One can iterate between the curves

y = x
y = r x(1-x)

For small r = 2.9 we get iteration to the "stationary point"

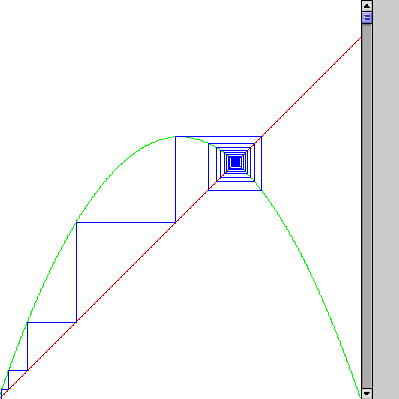For medium r = 3.16 we get a "period 2"

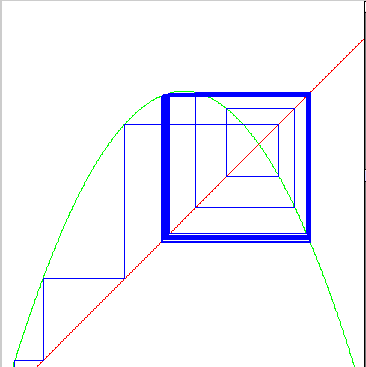For slightly larger r = 3.59 we get a "period 4"

For large r = 3.66 we get chaos

Assignment: these come from a web-site

http://math.la.asu.edu/~chaos/logistic.html

Go to this site and experiment to find the exact value at which period doubling starts, and which the period 4 starts and see if you can find a period 8 solution.

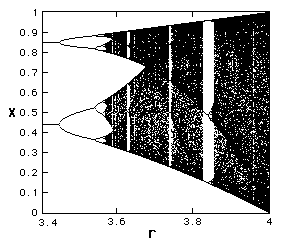
It is possible to plot the period: this is a "bifurcation diagram"

and we can look at this in a bit more detail:

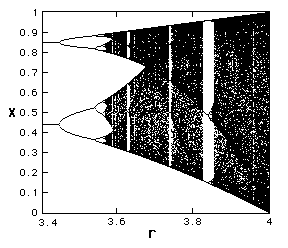What was totally unexpected was that such a simple system could have such a complex behaviour. Note that period doubling repeats itself, after chaos sets in there are still regions of the parameter r for which the solution is simple!

A physical example the "chaotic pendulum". Small swings are predictable,

Medium ones are quasi-periodic

large are not.

The most famous example is weather. "Primitive Equations" written down by L F Richardson (1922). Can't be solved without computer

“After so much hard reasoning, may one play with a fantasy? Imagine a large hall like a theatre, except that the circles and galleries go right round through the space usually occupied by the stage. The walls of this chamber are painted to form a map of the globe. The ceiling represents the north polar regions, England is in the gallery, the tropics in the upper circle, Australia on the dress circle and the antarctic in the pit.

A myriad computers are at work upon the weather of the part of the map where each sits, but each computer attends only to one equation or part of an equation. The work of each region is coordinated by an official of higher rank. Numerous little "night signs" display the instantaneous values so that neighbouring computers can read them. Each number is thus displayed in three adjacent zones so as to maintain communication to the North and South on the map.

(computers in old fashioned sense of someone who computes!)

From the floor of the pit a tall pillar rises to half the height of the hall. It carries a large pulpit on its top. In this sits the man in charge of the whole theatre; he is surrounded by several assistants and messengers. One of his duties is to maintain a uniform speed of progress in all parts of the globe. In this respect he is like the conductor of an orchestra in which the instruments are slide-rules and calculating machines. But instead of waving a baton he turns a beam of rosy light upon any region that is running ahead of the rest, and a beam of blue light upon those who are behindhand.

Four senior clerks in the central pulpit are collecting the future weather as fast as it is being computed, and despatching it by pneumatic carrier to a quiet room. There it will be coded and telephoned to the radio transmitting station. Messengers carry piles of used computing forms down to a storehouse in the cellar.

In a neighbouring building there is a research department, where they invent improvements. But these is much experimenting on a small scale before any change is made in the complex routine of the computing theatre. In a basement an enthusiast is observing eddies in the liquid lining of a huge spinning bowl, but so far the arithmetic proves the better way. In another building are all the usual financial, correspondence and administrative offices. Outside are playing fields, houses, mountains and lakes, for it was thought that those who compute the weather should breathe of it freely.” (Richardson 1922)

The "Lorentz" equations: this is a very simplified version of the equations that describe weather.
These give rise to chaotic behaviour: hence it is plausible that weather itself is chaotic.
You cannot predict the future weather precisely. However, buried in this are some predictable elements.
e.g. we cannot predict an "el Nino" event, but we can predict the consequences once it has happened.
Note "weather" prediction and "climate" prediction are (almost) unrelated

But we can still predict weather in the short term

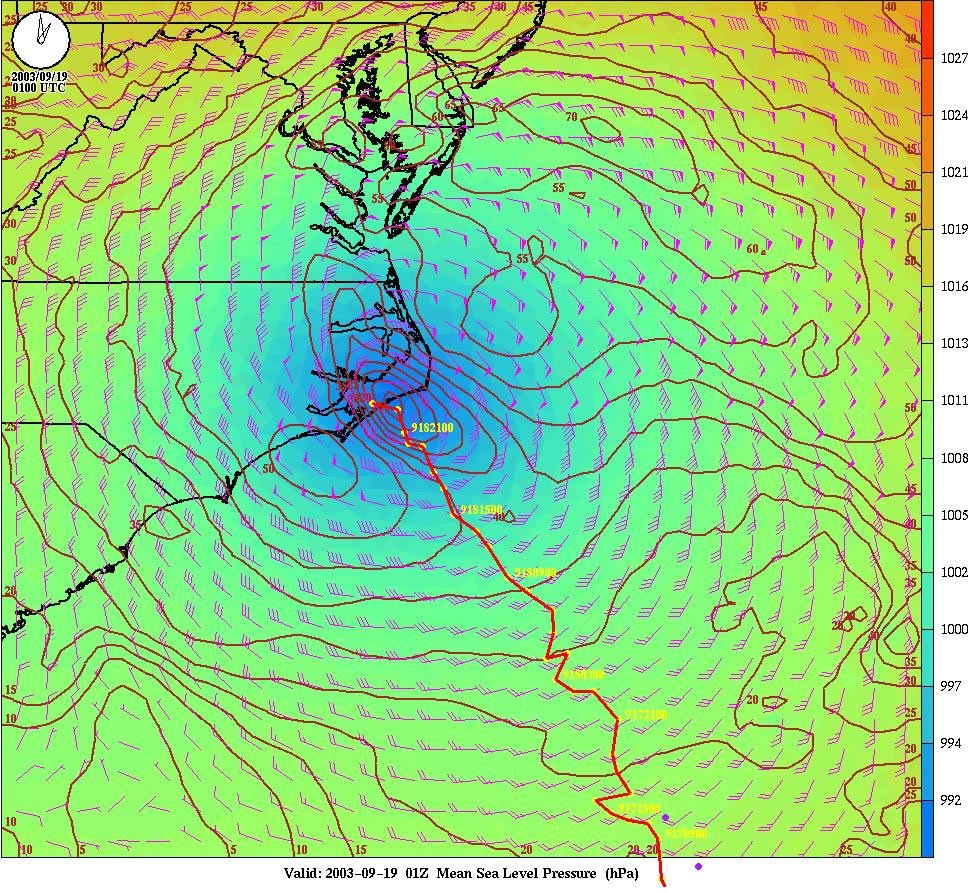George Mason U camp.gmu.edu/significant_ weather_prediction.html

And this is what Hurricane Isabelle actually looked like!

Now we know enough to look at The Universe