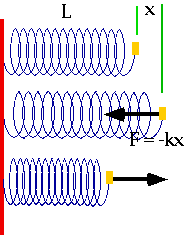
| Hooke's Law extension ∝Force, or F = -kx |
 |
| A drumhead (Talman, MCSD Denver) |
There are many forms of oscillatory motion is nature: e.g.
| Hooke's Law extension ∝Force, or F = -kx |
 |
F = -kx
| Watch the simulation |
Then Newton's 2nd law can be used
F = ma = - kx |
 |
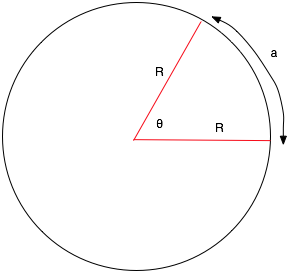
| S.H.M. is "half" of rotational motion. |
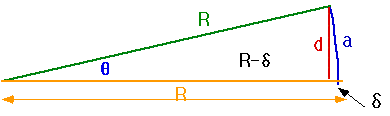
θ = a
R
For these relations, we can work in either of
|
 |
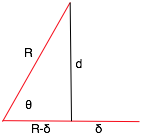
A useful mnemomic SohCahToa
Sin = opposite = d
hypotenuse R
Cos = adjacent = R-δ
hypotenuse R
Tan = opposite = d
adjacent R-δ
|
|
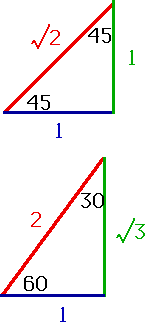
Special Values
|
|
We often have a convenient simplification when the angles are small
θ = a/R ~ sin(θ) = d/R cos(θ) ~ 1Note that this only works if we measure angles in radians: |
 |
ω = 2πf
| Formally, we can write
\color{red}{
\begin{array}{l}
x = A\cos \left( {\omega t} \right) \\
y = A\sin \left( {\omega t} \right) \\
\end{array}}
for circular motion (because θ = ωt). |
acceleration = -constant * displacement
Watch the animation.
In this case, tension in string supplies force to return bob to centre
a = -g x
L
with the same solution as before x = A sin(ωt)or (better) θ = θ0 cos(ωt) |
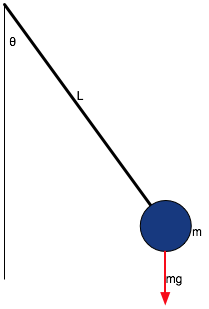 |
ω2 = g/L
f = ω/2π cycles/s = ω/2π Hz
P = 1 = 2π = 2π(L/g)1/2
f ω
U = 1/2 k x2
| Note that the P.E. is positive for x < 0 as well as x > 0: you can store energy in a stretched spring or a compressed spring. | 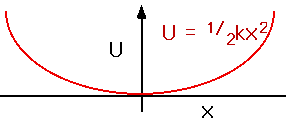 |
P.E. = 1/2 k x2 K.E. = 1/2 m v2 Total Energy = 1/2 k x2 + 1/2 m v2 |
 |
y = y0e-atsin(ωt)The frequency is almost the same, but the amplitude decreases exponentially with time
| a pendulum swinging in vacuum: almost undamped (a = 0.1 small) | 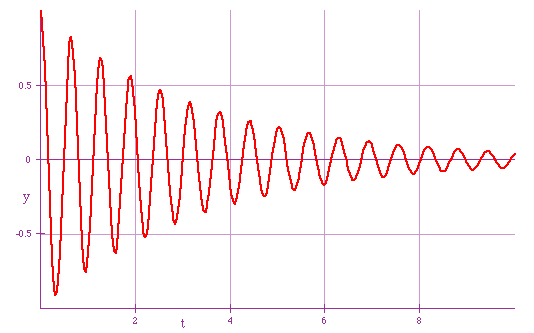 |
| a pendulum swinging in syrup: will not complete one swing (a = 1.0 large) | 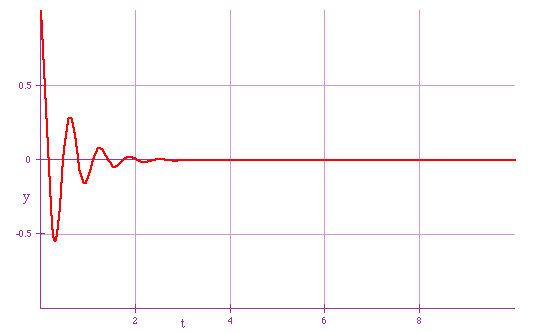 |
Up to now, we have assumed that the system is started off at some time and allowed to oscillate. However, can arrange for the system to be driven, so that driving force varies in time. Watch the demo:
If driving frequency ω0 matches natural frequency of system ω, then size of oscillations grows
Usually some damping, so does not grow without limit. e.g.
From: "MIDN Zamberlan" <m017107@usna.edu> To: <watson@physics.carleton.ca>
Subject: Answering a rhetorical question
Date: Fri, 17 Nov 2000 01:28:03 -0500 X-Priority: 3
Very respectfully,
RJ Zamberlan MIDN, USN