Kinematics








  • Comet Mcnaught from Herzberg building
  • Date: January 10, 2007
  • Author: Etienne Rollin

The Description of Motion

Motion

Normally we would be concerned with starting from some fundamental axioms and deriving a set of equations which allow us to handle real-world problems. We will skip about 2/3 of this,and work on a "need-to-know" basis. If you want to see a more systematic derivation, look here.
We start by describing motion

Speed and Velocity

Average Speed is just distance/time 
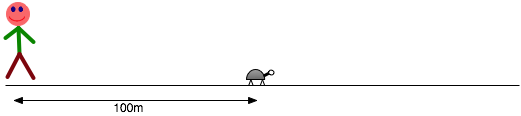
Speed =  d  
       (t1-t0)

e.g. if Achilles runs d=100m starting at 4.00.00 p.m. and ending at 4.00.20 p.m., then 

speed = 100  = 5 ms-1
      (20-0)

Displacement is the distance that you end up away from the starting point (Not the total distance travelled)

Velocity is Displacement/time

Displacement and Distance

Constant Acceleration

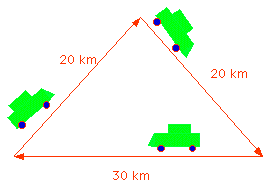e.g. A car travelling between traffic lights
. Lights are 25 m apart, and the car takes 10 s to travel between them, by accelerating to start with and then braking at the same rate.

Distance-Time plot

Note that car starts slowly: position plot draws out a smooth curve 
Av. Vel. (0-10 s) = Tot. Dist.  = 25  = 2.5 ms-1
                    Tot. Time     10
Suppose we take a 4 s time window 
Av. Vel. (4-8 s) = Tot. Dist.  = 14  = 3.5 ms-1
                   Tot. Time     4
Suppose we take a 2 s time window 
Av. Vel. (4-6 s) = Tot. Dist.  = 9  = 4.5 ms-1
                   Tot. Time     2

Instantaneous Velocity

Av. Vel. over short time => Instantaneous vel. = slope of dist/time curve

Instantaneous Velocity

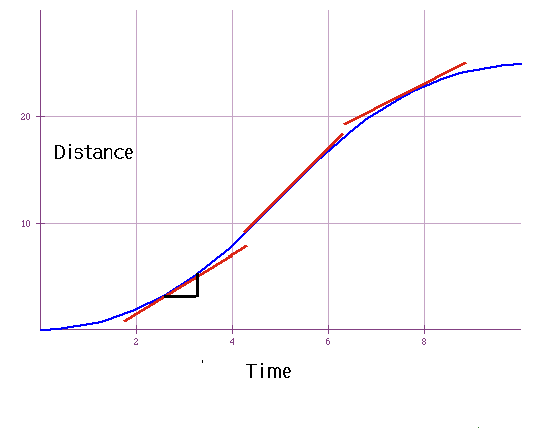
This is in fact an example of constant accn. Instantaneous vel. = slope of dist/time curve

= 5 ms-1 at t = 5 s

Velocity-Time plot

By measuring the slope at each point, we can get the velocity time curve.

Acceleration

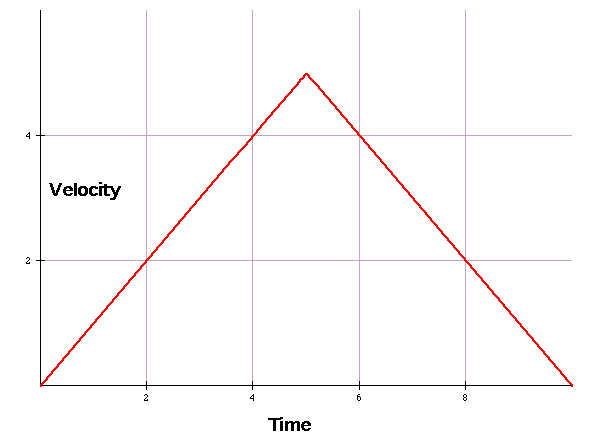
a = change in velocity
             Time


a = (v1-v0)  = δv   = dv
    (t1-t0)    δt     dt

Acceleration-Time plot

This is easy for the case we are considering... 
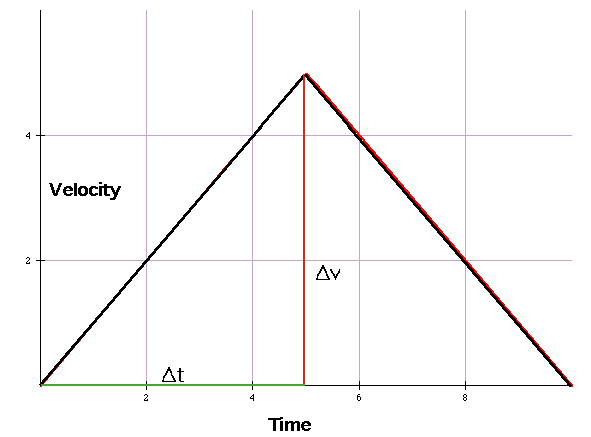
a = (v1-v0)  = 5  =1
    (t1-t0)    5

Acceleration

For 0<t<5

a = 5/5 = 1 ms-1 i.e. or any time t < 5s, the accn is the same:

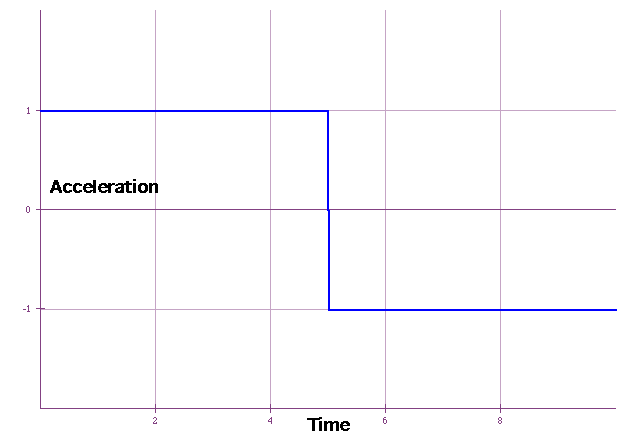
(note the Greeks had no concept of accn.)

Constant Acceleration

Often a very good approximation $$ \color{red}{ a = \frac{{{\text{change in velocity}}}}{{{\text{change in time}}}} = \frac{{v_1 - v_0 }}{{t_1 - t_0 }}} $$

If we start the clock at t0=0, when the velocity is v0, then this can be written

$$ \color{red}{ a = \frac{{v - v_0 }}{t}} $$ or $$ \color{red}{ v = v_0 + at} $$

i.e. vel at time t = starting vel + accn*time Similarly, we get the average velocity

$$ \color{red}{ \bar v = \frac{{v + v_0 }}{2}} $$

but this is also total distance/time = s/t Hence

\color{red}{ \frac{s}{t} = \frac{{v_0 + at + v_0 }}{2}}
which can be re-arranged

$$ \color{red}{ s = \bar vt = \left( {\frac{{v_0 + at + v_0 }}{2}} \right)t = v_0 t + \frac{1}{2}at^2 } $$

v-s

Finally we can combine eliminate time from these two equations
\color{red}{ \begin{array}{l} s = v_0 t + \frac{1}{2}at^2 \\ t = \frac{{v - v_0 }}{a} \\ \end{array}}
so that
\color{red}{ s = v_0 \frac{{v - v_0 }}{a} + \frac{1}{2}a\left( {\frac{{v - v_0 }}{a}} \right)^2 }

After tidying $$ \color{red}{ v^2 = v_0 ^2 + 2as} $$

Summary

These three equations are very useful
\color{red}{ \begin{array}{l} v = v_0 + at \\ s = v_0 t + \frac{1}{2}at^2 \\ v^2 = v_0 ^2 + 2as \\ \end{array}}

These only apply if the Acceleration is constant: do not use otherwise!

Gravitation

A very important example of this is the acceleration due to gravity.
Next we need to understand motion in terms ofForce