Cosmology 2: Dark Matter

So how do we weigh the universe?

5) There is still a big dark mystery out there

There is only a single God, Mixcoatl, whose image they posess, but they beleive in another, invisible, god, not represented by any image, called Yoalli Ehecatl, That is to say, God Invisible, Impalpable, Benificent, Protector, Omnipotent by whose streght alone...rules all things

Nahuatlan Myth

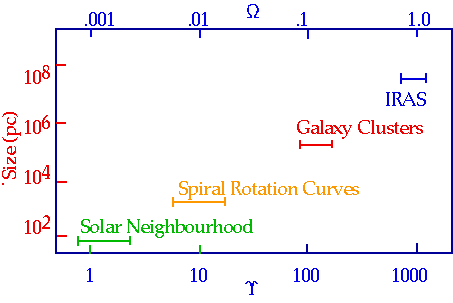
Can only see luminous matter: how much Dark Matter is there? Usually expressed as mass to luminosity ratio (Upsilon) Υ = M/L; For sun

Υ₀ = M₀/L₀ ≈ 5000 kg/W

1. First Guess: What you see is what you get!

   Count number of galaxies in a region of space, assume they consist of stars much like the sun, so
   

   Υ = M/L  = M₀/L₀
   

   Obviously must average over large enough volume such that universe is smooth R > 100 Mpc, and the universe is a very lumpy place!

   => Density:

   Ω = ρ ~ .001      
         ρ₀ 
   

   Note all these numbers are uncertain to ± 50%!)

   We live forever!!!
   But wait a moment...

   How much matter is there we that we can't see? This assumes ρ_dm ~ 0

2. 1^st order estimate:

   based on loose estimates of dark nebulae, obscuration of light and dust seen in other galaxies

   ρdm  ~ 1  so M ~ 2M₀ 
   ρlum              L      L₀
   

3. Local Dynamics:

   Can get estimate of local density by motion of stars

   ρdm  ~ 2  so M ~ 3M₀ 
   ρlum             L       L₀
   

   (first direct evidence for D.M.)

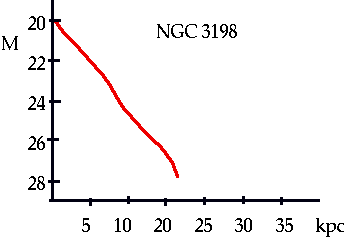
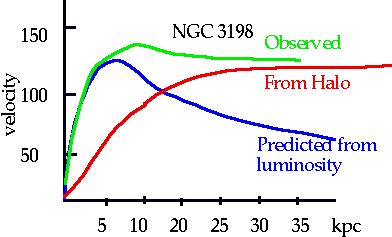
4. Masses of Spiral galaxies

   direct observation i.e. measurement of velocities of individual stars in nearby => rotation curves or measurement of hydrogen via 21cm line or estimates of no. of stars
   Luminosity of galaxy should reflect mass
   Typical Spiral (NGC3198) R ≈ 20 kpc but outer parts are just seen as H gas
   Should be able to calculate rotational speed In core of galaxy, mv²/r1 = G M(r1)m/r1² M(r1) is mass inside orbit: total mass M =⁴/3 πR³ ρ and M(r1) = ⁴/3 π r1³ ρ = M r1³/R³ Hence inside core: v²/r = G Mr³/(r²R³) or v = (GMr²/R³)1/2 Outside core: mv²/r = GMm/r² or v = (GM/r)1/2
   Most of the light is fairly concentrated, so this should be good approx to the mass. These show rotation curves i.e. velocity curve doesn't drop as expected
   Can fix this by saying that galaxy has halo of dark matter around it. Hence outside core but still inside halo force = force due to core + force due to halo v²/r = GM/r² + G M'r³/(r²R'³) or v = (GM/r + GM'r²/R'³)1/2

   ---

   Not perfect: by fitting we can get a better result Halo + core add together to give correct curve
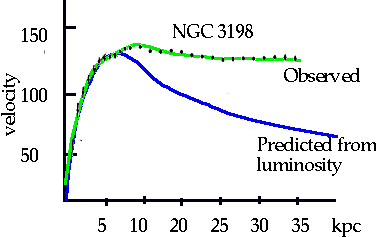   Note this is not unique to NGC 3198: all measured spirals show same. (Have to have spiral that is not "flat on", since no Doppler, or "side on" since cannot separate different parts)

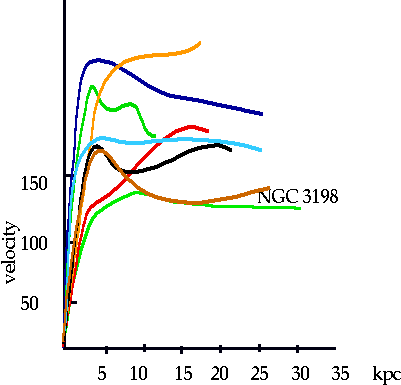   For spirals

   10 M₀ < M <40 M₀
        L₀       L        L₀ 
   

   Implication:

   Mass of observed galaxy ≈ 10¹⁰ M₀, R ≈ 2 kpc (for core)
   Mass of halo ≈ 10¹³M₀, R ≈ 100kpc (except that we can't measure out there!)

   What do we mean by mass of galaxy? In fact the visible part of the galaxy may just reflect the dark matter.

   ---

5. Large clusters of galaxies:

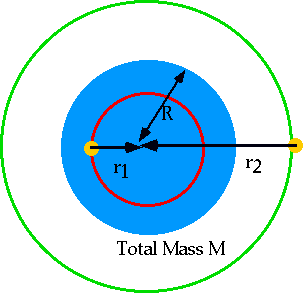
   By measuring vel. cpt. in line of sight (via Doppler) can get estimate of M

   <K.E.> = -1/2<P.E.> 
   

   Just like measuring mass of a planet via orbits of its moons, except that
   
   1. the mass isn't all concentrated at the centre
      
   2. can only measure velocity in one direction
      
   3. must assume that the peculiar velocities cancel out.

   ---

   This gives much higher masses than indivdual spirals
   

    M ~ 100M₀ ,  Υ≈ 100-1000Υ₀
    L           L₀  
   

   Can use Hydrostatic Equilibrium equation & Eqn. of State to estimate mass (just as we did with stelar modelling
   

   dP = -Gm(r) ρ(r), P =  kρT
   dr         r²                      μm
   

   
   hence can measure m(r) which is the mass attracting the more distant gas
   

   M ≈ 8x1014 M₀  ⇒ Υ = 300Υ₀
   

   for Coma

   A check: Large clusters contain a lot of hot gas, which is strong X-ray source X-ray pictures measure density and temp:

   This gives much higher masses than individual spirals.

   Also large clusters show gravitational lensing, can get quantitative estimate

6. IR sky surveys suggest that the total mass may be much higher

Note that the larger the object, the more massive (proportionately) that it is.

a) What the hell? i.e. what is the dark matter?

b) Why the hell? i.e. why is Ω~1 (after all it could be anything?)

Actually, there is a limit

Ω < 3 

otherwise the universe would be younger than the earth (wouldn't that make the creationists happy!!)

What the hell:

1. Brown dwarfs
2. Hydrogen gas
3. Jupiters
4. Hydrogen rain
5. Low surface brightness galaxies
6. Maxi Black holes
7. Mini Black holes
8. Neutrinos
9. He H ⁺
10. Modified 1/r² law
11. Axions
12. Weakly Interacting Massive Particles (WIMPS)
13. Magnetic Monopoles
14. Majorons
15. Photinos
16. E₈ shadow matter
17. Cosmic Strings

Which is it? We don't know! However, all of the above have problems.

The Generic Candidates for Dark Matter :

1. Baryonic (BDM) ordinary matter, but maybe in some odd form e.g. rocks
2. Hot (HDM) particles which were relativistic at time of BB e.g. ν's
3. Cold (CDM): heavy (usually) particles e.g. WIMPs
4. Mixed (MDM) e.g. 70% WIMPs, 30% ν's
5. Decaying Dark Matter (DDM)

We'll see later that primordial concentrations gave Ω_B ≈ .06--.1 (Much too low!!!)

i.e. the dark matter cannot be all "normal" baryonic matter.

Neutrinos

ρc≈ 5×10-27 kg m-3 ≈ 5 GeV m-3,  Nν ≈ Nγ ≈ 109 m-3

mν ≈ 5 eV ≈ 9×10-36 kg (≈ 10-5 me)

It's more complicated (you were surprised?) There are three kinds of ν's, and the correct result is that

Σ mi ≈ 30 eV.

However, it is not possible for all of dark matter to be ν's: we need a fraction of CDM particles. How are we going to see the black-body ν's??(Ass. 6 fills in the blanks in this argument)

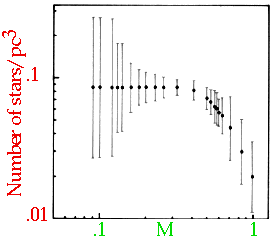
MaCHOs

If Ω = .01 in luminous stars +BDM, would need 100 × mass in non-luminous objects to reach Ω = 1
If mass = .01M₀ (high), we would need 10⁴ Brown Dwarves for every "normal" star, or 10⁵ Jupiters

We need to search for stars in IR (T ≈ 1000K) None in our neighbourhood.
would need

Maybe several brown dwarfs were found

Microlensing

If one star passes in front of another, we cannot see a double image (as with quasars), but we can see brightening as the BD passes across a star's image.

The predicted rates are reasonable:

Distinguishing them from variables: Must be symmetrical, achromatic, single, on-off events.

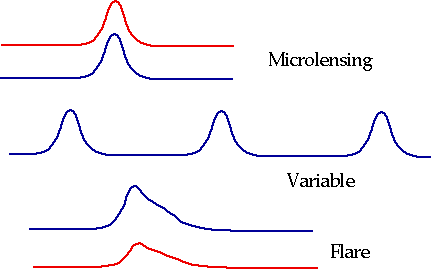The Experiments

Eros, ≈ 10⁶ stars.
Macho, 300 digitized plates + CCD

Macho 1 "Gold-plated" event
M = 19.55
A = 6.8
τ ≈ 33.8 days

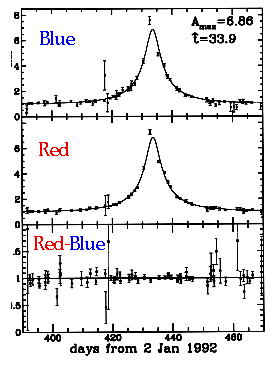
This event was also seen (but not completely) by EROS: Consistent with M = .1M₀ and with Ω ≈ .1 and with all of halo consisting of these.

Hydrogen gas:

Can't see 21cm Line, so would have to be very diffuse (<.1 atom m^-3) which doesn't solve the problem

Hydrogen rain

(Boiling point of H₂ is 22K)

Could exist in molecular clouds, but cannot explain clusters of galaxies.

Low surface brightness galaxies

Galaxies as big as (e.g. M31) but with only 10⁷ stars would be invisible.

Number of these now known in local group

Not enough near us

Black holes, mini/maxi

Maxi: say 10⁸ M₀: Only occur in centre of galaxies (?). Created during active (quasar) stage of galaxies

Mini: M ≈ 1 M₀, Created during Big Bang Not made in large enough numbers (Hawking)

No-Nameons: CDM candidates

• Axions
• Majorons
• Weakly Interacting Massive Particles
• Photinos
• LSP's (Lightest supersymmetric particles)
• Magnetic Monopoles
• E₈ shadow matter

....and there is a tooth fairy

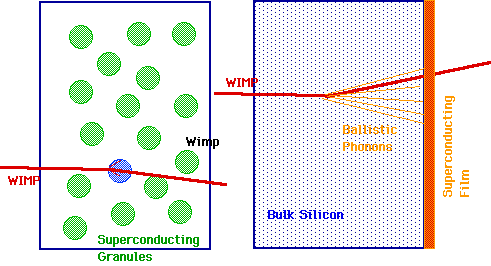
Although these are similar cosmologically, they are very different from the point of view of detection. A lot can be ruled out by "in vitro" experiments (e.g. OPAL at CERN puts limits on LSP's

Generic WIMPS can be seen "in vivo" via a variety of low temp. expts.: e.g. Queens expt, U de Montreal expt. Nucleus will recoil and transfer energy to lattice, flipping superconductor or sending off ballisitic phonons. So far, no results!

Collect your Nobel prize on the way out........

We are left with two major problems

2) Why is the universe large and flat?
It has a natural size which is very much smaller, and there is no reason to have Ω=1 (this is the "Why the hell" question!). Remember for Ω = .1 today it must have been 1-10^-60 to start with. Its safer to assume that Ω=1 always.

3) Why is the universe all the same temperaature?
(the horizon problem) Bits of it have never communicated.

Why the Hell?

Why is Ω = 1 so important?

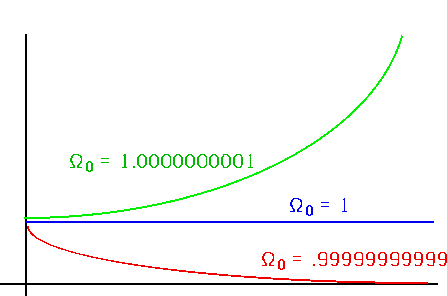
Since we now measure Ω ~ 0.1, this means that at the time of the BB it must have been ~ 1 - 10-60 i.e. Ω = 1 is an unstable critical point The flatness problem is worse than you would think: If the universe started out at 10-44 s with (say) Ω = 3, it would last ≈ 10-35 s (!!!!)

Now for the rest of the story: we need to look at the Big Bang in detail?