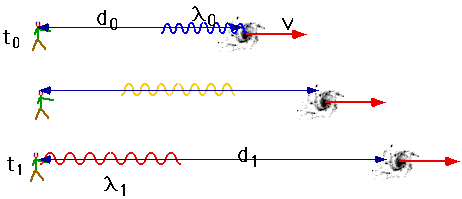
At time t₀, a galaxy is at a distance d₀ from us, and is travelling at v
We see the photon at time t1
From the (incredibly naive) model we can deduce:
Connection between time, distance and red-shift:
At time t₀, a galaxy is at a distance d₀ from us, and is travelling at v We see the photon at time t1 |
 |
In time t between γ emission & absorption, the distance has increased (universe has expanded) by zct. so γ has to travel further:
travel time
t = d1/c
so
d1 = d₀ + zct = d₀ + zd1 so that d1 = d₀/(1-z) (non-relativistic)
i.e. if z = .25, the universe was 75% of current size when γ was emitted
(Note we have made a subtle change in the description: it is not the other galaxy which is moving away, it is the space in between which is stretching!)
We can also relate red-shift and age: At t = 0, universe had no size so
d₀ = vt₀ = zct₀ hence t₀/t1 = d₀/d1 = (1-z)
so that
t₀ = t1(1-z)
so again if z = .25, the universe was only 75% of its current age
(Correctly d1 = d₀(1+z) and t₀ = t1/(1+z), because of relativistic effects, but we also need to allow for slowing down of the expansion)
To make this look a little fancier, we will introduce the "Cosmic Scale Factor", R(t). All distances will scale by the same amount, so we can define:
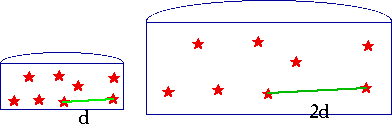
r(t) = σR(t) σ is a dimensionless number, which does not vary with time. If you like, σ=r(t=0). In this case, r₀ = d, r = 2d so R= ..? |
 |
This means that instead of talking about the distance between all the galaxies varying as a function of time, we can extract all of the time variation and put it into one parameter.
Note some relations:
$$
\color{red}{
v\left( t \right) = \frac{{\partial r\left( t \right)}}{{\partial t}} = H\left( t \right)r\left( t \right) = \sigma \frac{{\partial R\left( t \right)}}{{\partial t}} = \sigma H\left( t \right)R\left( t \right)}
$$
(since σ doesn't change with time)
so $$
\color{red}{
\frac{{\partial R\left( t \right)}}{{\partial t}} = H\left( t \right)R\left( t \right)}
$$
(Note since σ is a dimensionless initial value, can use units system in which σ = 1, and drop it now.)
How does the density change in this model? ρ(t) = ρ(t₀) (R(t₀)/ R(t))³ = ρ₀ R₀³/R³ Note: we are talking about matter density here |
 |
SinceR(t) = Ct2/3 |
 |
In this model
∂R(t)/∂t = ²/3 C t-1/3
and hence $$ \color{red}{ H\left( t \right) = \frac{1}{{R\left( t \right)}}\frac{{\partial R\left( t \right)}}{{\partial t}} = \frac{2}{{3t}}} $$
If we take t as the time now since the Big Bang
t = ²/3 H-1 = 12x109 yrs
| The universe was originally opaque (i.e. mean free path of γ's very small) and hence CMBR was in thermal equilibrium with matter. Then the universe "condensed" (or froze) out. | 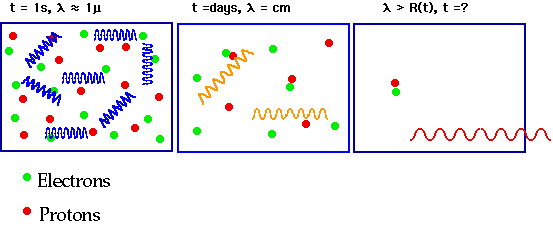 |
Thermal equilibrium between matter and radiation implies they are at the same mean energy, with a Black Body distribution of γ's.
Expansion ⇒ Cooling.
| Need the R dependence of energy density, ρ
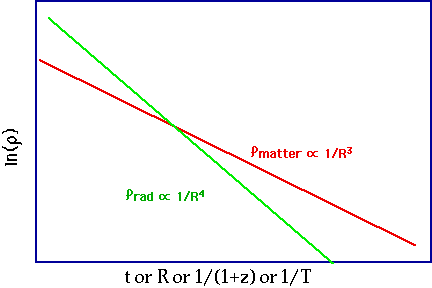
Non-Relativistic Matter (i.e. Baryons): ρ ≈ 1/R³(t) Relativistic particles (i.e. γ's, ν's) get red-shifted as well, so ρ ≈ 1/R⁴(t) We live in matter dominated universe ρmatter >> ρrad, |
 |
This is all a bit of a cheat, since we have assumed non-relativistic Newtonian mechanics: we should use General Relativity. However, we can do almost everything in terms of our (naive) model
To start with, we want the Friedmann equation
$$
\color{red}{
\frac{1}{2}mv^2 - \frac{{GMm}}{r} = E \to \left( {\frac{{\dot R}}{R}} \right)^2 = \frac{8}{3}\pi G\rho - k\frac{{R_0^2 }}{{R^2 }}}
$$
We will choose our scale so that k is an integer: the "curvature" of universe
k = -1 means E > 0, open, negative curvature
k = 0 means E = 0, critical, zero curvature
k = 1 means E < 0, closed, positive curvature
Also need the connection between $\rho$ and R: for matter and radiation we have argued $$ \color{red}{ \rho _M \sim \frac{1}{{R^3 }}:\rho _R \sim \frac{1}{{R^4 }}} $$
In general, if we have an expanding gas, change in energy = W.D. $$ \color{red}{ d\left( {\rho V} \right) = - PdV \to \frac{d}{{dt}}\left( {\rho \frac{4}{3}\pi R^3 } \right) = - P\frac{d}{{dt}}\left( {\frac{4}{3}\pi R^3 } \right)} $$
For cold matter, P = 0, so we get back the old result. For radiation:can repeat old kinetic theory of gases derivation giving P = 1/3 ρR. In general we'll write P = wρ. Then $$ \color{red}{ \frac{{d\left( {\rho R^3 } \right)}}{{dt}} = - w\rho \frac{{d\left( {R^3 } \right)}}{{dt}}} $$
Then $$ \color{red}{ \frac{{d\left( {\rho R^{3\left( {1 + w} \right)} } \right)}}{{dt}} = 0} $$ or ρR3(1+w) is a constant (prove it: hint first show $$ \color{red}{ \frac{{d\left( {R^{3\left( {1 + w} \right)} } \right)}}{{dt}} = \left( {1 + w} \right)R^{3w} \frac{{d\left( {R^3 } \right)}}{{dt}}} $$
Can now solve easily for flat universe $$ \color{red}{ \left( {\frac{{\dot R}}{R}} \right)^2 = \frac{8}{3}\pi G\rho _0 \left( {\frac{R}{{R_0 }}} \right)^n ,n = 3\left( {1 + w} \right)} $$
where n = 3 (matter) or 4 (radiation) or anything else
So we want the relation between t and T:
Expansion time:
α2 = 8/3πGρ
The Solution is............
$$ \color{red}{ \int {R^{n/2 - 1} dR} = \alpha R_0^{n/2 - 1} t \to R = R_0 \left( {\frac{{n\alpha }}{2}} \right)^{2/n} t^{2/n} } $$Hubble's "constant" is $$ \color{red}{ H = \frac{v}{d} = \frac{{\dot R}}{R} = \frac{2}{{nt}}} $$
Note: For small t, v(t) ≈ 1/R(t) >> c => the horizon problem. No immediate problem with relativity, (since no info is transferred but ...
Parts of the universe have never been in contact with each other. How do they know to be at the same temperature?
For k = 0$$ \color{red}{ \rho = \rho _c = \frac{{3H^2 }}{{8\pi G}}} $$
as we expect. If we have only radiation $$ \color{red}{ \rho = \frac{{4\sigma T^4 }}{{c^3 }}} $$
which gives an exact expression for the temp:
$$
\color{red}{
T^2 = \frac{1}{t}\sqrt {\frac{{3c^3 }}{{64\pi G\sigma }}} ,t = \frac{\xi }{{T^2 }}}
$$
As the peak in the BB curve falls below hydrogen binding energy, 1H forms, at ~3700 K, ie about 1/2eV. When did this happen?
(Note, this is less than the 13.6 eV that you would expect: need Saha equation)
When was the temp 3700K?...............This lets us calculate (an important number) cooling time to 3700Kτ ≈ ζ/T² ≈ 500,000 yrs, or 1+z ≈ T/T₀ ≈ 3700/2.736 ≈ 1360
What happens if the universe is not flat? we have to solve $$ \color{red}{ \int {\frac{{dR}}{{\sqrt {\frac{\alpha }{{R^{n/2 - 1} }} - k} }}} = t} $$
(see Berry for details: tedious but straightforward! Note thsi give us f(R) = t, not R = g(t) which we would like
As the universe expands, the density of γ's decreases.ρ(t) = ρ₀ R₀³/R(t)³ and also the temperature T falls as each γ gets redshifted |
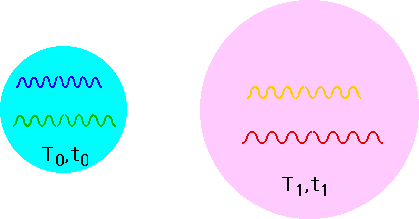 |
Hence the energy density E(t) ∝ R(t)⁴
More exactly: from the Black Body equation:
Energy density:
u = T⁴ × 8/15π5k⁴/(h³c³) = aT⁴ = 4σT⁴/c
Mean γ-energy E ≈ 2 x 10-4 T eV
actually = hc/λ = 6.58x10-16 x 3x108 /λ
Peak of BB curve is at λ = 2.898x10-3/T
Now, the peak is at 1.05 mm: what is the temperature, N, E, ρ?
When did the universe stop being radiation dominated?
We said: ρc ≈ 3 H/m³. We see less: ρM ∼≈ .01 H/m³. !!!
Better: energy in protons = (number/unit volume)×mc² Say
ΩM∼ .01 ⇒ EM ≈ 0.01×10MeV/m³ ∝ 1/R³
Energy in CMBR photons
Erad = 4σT⁴/c ≈ 0.4 MeV/m³ ∝ 1/R⁴
So these were equal when:
R(t)/R(t₀) = Ematter/Erad ≈ 1250 = (1+z)
ie, at about the same time that the universe became transparent. (Note: we began with a very large uncertainty, setting Ω ≈ 0.01, based on .03 proton per cubic metre: depending on the nature of the DM we can change this by a factor of 10)
This "light" is now at 2.736°K, and almost uniform in every direction. It was emitted just 100000 years after the Big Bang and has been travelling round the universe ever since. At time t₀, the universe is full of γ's at a temperature T₀.
One more special case: how about if vacuum itself has an energy ρv=Λ/3 ≠0? Λ is the cosmological constant "Einstein's greatest blunder"! Introduced as a fudge factor in 1919 to stop the universe from collapsing
Obviously $$ \color{red}{ \frac{{d\rho _v }}{{dt}} = 0} $$so (setting ρm= ρR=0 for simplicity) we can use $$ \color{red}{ \left( {\frac{{\dot R}}{R}} \right)^2 = \frac{\Lambda }{3}} $$
which is our previous results with w = -1: this gives$$ \color{red}{ \left( {\frac{{\dot R}}{R}} \right)^2 = \frac{\Lambda }{3},R(t) = R_0 e^{\sqrt {\frac{\Lambda }{3}} t} } $$
i.e. the universe expands exponentially. Why would we want this?
6) Fortunately there is a special place for us
And God said " Let us make man in our own image, after Our likeness, and let them have dominion....over all the earth
Genesis I.26
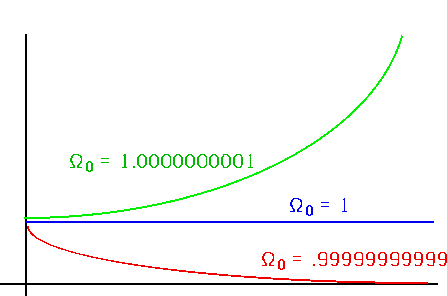
Why is Ω = 1 so important? Combining
$$ \color{red}{ \dot R^2 = \frac{{8\pi G\rho _0 }}{{3R^{n/2 - 1} }} - k,\Omega = \frac{\rho }{{\rho _c }} = \frac{{8\pi G\rho }}{{3H^2 }},H = \frac{{\dot R}}{R}} $$ gives $$ \color{red}{ 1 - \frac{1}{\Omega } = \frac{{3k}}{{8\pi G\rho R^2 }} = \frac{{3k}}{{8\pi G\rho _0 }}R^2 } $$ (LHS is fractional deviation of Ω from 1)Why is Ω = 1 so important?
| Since we now measure Ω ~ 0.1, this means that at the time of the BB it must have been ~ 1 - 10-60
i.e. Ω = 1 is an unstable critical point The flatness problem is worse than you would think: If the universe started out at 10-44 s with (say) Ω = 3, it would last ≈ 10-35 s (!!!!) |
 |
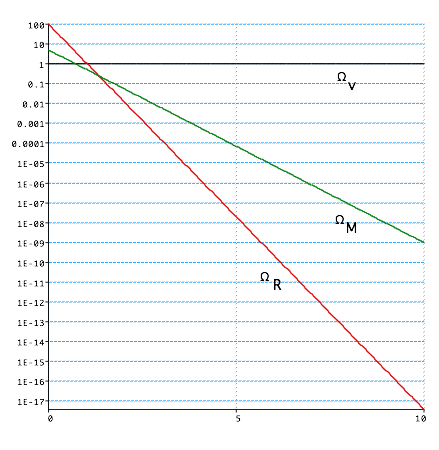
Need to separate the 3 contributions to Ω:
|
 |
| consider a very small volume of the (original) universe.
e.g. at t = 10-34 s, the size of the horizon is d = ct = 10-23 cm (≈ 10-8 size of a proton) The inflationary phase leads to an increase in the size of universe by 1080 (effect is very like continuous creation, in that the energy density remains the same). |
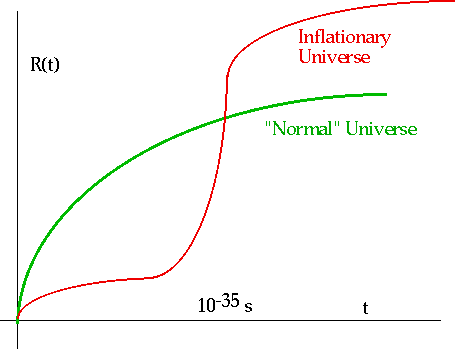 (diagram not exactly to scale!) (diagram not exactly to scale!) |
| An inflationary phase "smooths out the wrinkles". The temperature in this volume was already in equilibrium. Now, after inflation, it is much larger and smoother than before. | 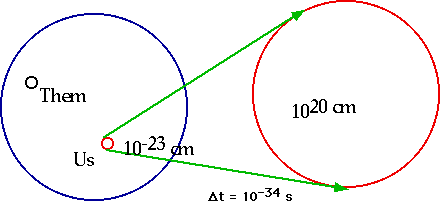 |
At 10-35 s, the universe could not have deviated very much from Ω = 1.
After inflation, the density hasn't changed (remember steady state model?) but the universe is 1043 times larger. Need to turn off inflatio at thsi time: introduce some new, very heavy particle which will decay, both stopping inflation and creating matter and radiation at the critical density.
This means that it can never deviate much from Ω = 1.
Before finishing this off, we really need to the calculation more honestly: i.e. using General Relativity