
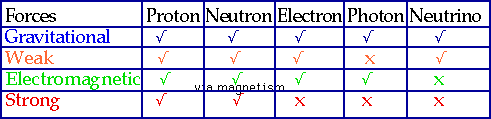
| Strong force is the force that binds together nucleons to make nuclei, weak force is force that causes β-decay. Believe there are only 4 forces in nature |  |
Note: "feels" means that this is what the force couples to: e.g. gravity does not care whether a particle is charged, only whether it has mass.
Range: if it is ∞ then F ∝ 1/r², else it cuts off at distance shown
Strength: roughly the relative strength of the forces at a distance of 1 fm.
Although (e.g.) strong force>>>E.M at 1 fm (=10-15 m), it vanishes totally beyond 10-14 m. E.M >>> Gravity, but it tends to cancel out since most matter is electrically neutral, whereas mass accumulates.
The weaker the force, the more particles feel it!
Particles: of the 450 (or so) elementary particles, only 5 are important to nuclei
| Strength also gives us (very roughly) the depth that a particle will penetrate matter without interacting:
e.g. a proton will penetrate a few mm, a X-ray photon a few cm, a neutrino several parsecs! |
 |
For every particle, with given quantum numbers, there is a corresponding anti-particle with the properties flipped:
e.g. electron has charge -1.6x10-19 Coulomb.
Positron has same mass, charge = 1.6x10-19 C
What is energy of γ? (1.6726+1.6749-3.3436)x10-27 x (3x108)² = 3.5x10-13J ∼ 2.2MeV |
Usually easier to quote elementary particle masses in terms of energy, measured in eV.
e.g. "mass" of electron =
mec² = 9.1x10-31x(3x108)² / 1.6x10-19 eV/Joule = 511 keV = 0.511 MeV
Usually (from point of view of astrophysics) means that reactions are:
2 bodies ⇒ 2 bodies
e.g. p + n ⇒ d + γ is allowed
p + n ⇒ d (where the d moves off with the extra energy) is forbidden.
n ⇒ e- + γ is forbidden: Algebraic sum of charges at end of reaction must = sum at start
Usual to use units where charge on electron is -1: i.e. 1 electronic charge q = -1.6x10-19 C
note γ ⇒ e+ + e- is allowed
The process p ⇒ e+ + γ is not forbidden by anything: however experimentally it does not occur:
No of (protons + neutrons) is always the same in a reaction:
Easiest to say that p & n carry baryon number B = 1, rest carry 0
Number of (electrons + neutrinos) is conserved
L is lepton number = 1 for electrons,
-1 for positrons
(-ν means anti-neutrino: what is an anti-neutrino? one with L = -1).
Mainly important because some particles carry spin ½:
e.g. n ⇒ p + e- is not allowed since
½ ⇒ ½ + ½ requires creation of angular momentum.
Instead n ⇒ p + e- + ν
½ ⇒ ½ + ½ + (-½)
| These conservation laws let us make up an extended particle table. The numbers are all conserved: e.g. why doesn't n ⇒ p e- γ happen?" |  |
| Lepton # | Charged lepton | Lepton mass | Neutrino | Sample Reaction |
| Le | e- | .511 MeV | νe | n ⇒ p + e- + ν̄e |
| Lμ | μ- | 105MeV | νμ | μ- ⇒ e- + ν̄e+ νμ |
| Lτ | τ- | 1784 MeV | ντ | τ- ⇒ μ- + ν̄μ+ ντ |
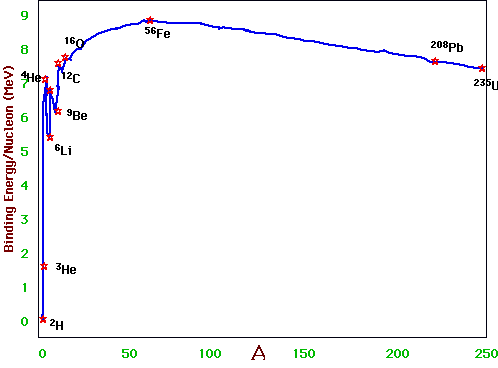
The only extra ingredient we need for astro-nuclear physics is the stable nuclei and their binding energies:
e.g. we saw that the deuteron was stable: the state (pp) is not: Rule of thumb: stable nuclei need Number of protons ∼ number of neutrons
If a nucleus has too many neutrons, one will decay via n ⇒ p + e- + -ν̄ (this is a β decay).
If it has too many protons, it will decay via p ⇒ n + e + ν
Note that there are no stable elements of A = 5 or A = 8
Since stars get their energy via nuclear reactions, the most important curve is binding energy vs A (Put differently): fusion reactions can occur for light elements, since medium-heavy elements are more stable, and fission reactions can occur for heavy elements, since medium-heavy elements are more stable. |
 |
⁴He + p ⇒ 5Li doesn't happen (5Li is unstable)
⁴He + d ⇒ 6Li is endothermic (i.e. won't normally happen)
Star starts off as H + ⁴He: what reactions can occur?
p + p ⇒ ²He can't occur,
p + p ⇒ d + e+ + ν is the initial process, and is very slow (the ν has only weak interactions, and so the whole process must go by that)
Once past this, the reactions are simple:
p + d ⇒ ³He + γ
d + ³He ⇒ ⁴He + p (or various variations: see later)
Most important is the "executive summary" 4 p ⇒ ⁴He + 2 e+ + 2ν + 27 MeV
Comments
Typical chemical reaction has E ∼ few eV/molecule (i.e. about 106 times less energetic)
Maximum efficiency of sun: if all of H was converted into He, η ∼ 27 / (4x939) ∼ 0.7%
Why do stars need to be hot (or why is there no cold fusion?)
There is a large repulsive E.M. force at large distances between two protons: only if r <1 fm is the force attractive (fm=femtometre =fermi =10-15m)
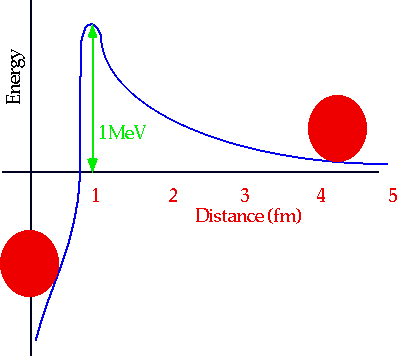
Height of this barrier is
E = 2Z1Z2e²/r, about 1 MeV
Hence to "ignite" thermonuclear fusion, it would appear to need temp ∼ 1MeV, which is E = ³/2 kT, so
T ∼ 8x109 K
This is temp reached in H-bomb: however the sun can work more slowly!
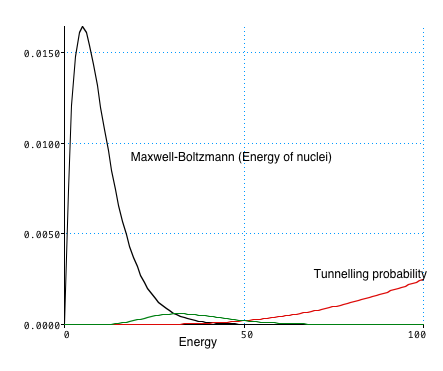
| Quantum Mechanics tells us that particles can tunnel through barrier:
For a particle of given energy, Probability of tunnelling P(E)∝ exp(-1/√ E) which gets larger for large E However there are very few nuclei with this energy |
 |
Ignition Temp T₀∼ 107K
Rates depend very strongly on temp and charge of nuclei: e.g. for pp, R ∝ (T/T₀)⁴
| Actual processes depend on what nuclei are stable: note that (e.g.) ³H is unstable, but sufficiently long-lived to be stable from the point of view of solar processes |
p + p ⇒ d + e+ + ν p + d ⇒ 3He + γ 3He + 3He + γ ⇒ 4He + p + p + γThe "executive summary" reaction converts hydrogen into helium
4 p ⇒ 4He + 2 e+ + 2ν
There is also a process that goes on in hotter stars, the CNO cycle
12C + 1H ⇒ 13N +γ
13N ⇒ 13C + e + ν
13C + 1H ⇒ 14N + γ
14N + 1H ⇒ 15N + e + ν
15N + 1H ⇒ 12C + ⁴He
Note that the 12C is a catalyst: the end product is
4 p ⇒ 4He + 2 e+ + 2ν
Past H burning, there are various processes that build up heavier nuclei: the crunch comes at A = 8: 8Be is unstable (τ ∼ 10-16 s) but Triple-α process occurs:
⁴He + ⁴He + ⁴He ⇒ (8Be) + ⁴He ⇒ 12C
Since three particles are involved, Rate ∝ ρ² (Two body reactions ∝ ρ) Means only happens at high (>108K) temps and very high pressures
| Beyond 12C processes add whole nuclei until we get to Fe |