- How do we know if it is true?
- Look for the ν's!
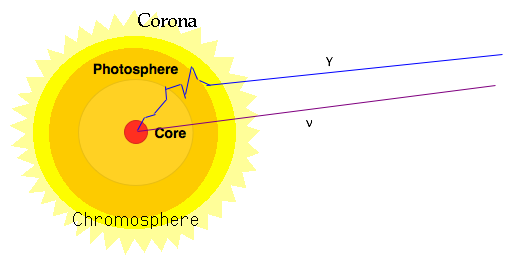
Star starts off as hydrogen (90%) + helium (10%) + 1% of everything else: what happens? The "executive summary" reaction converts hydrogen into helium
4 p ⇒ 4He + 2 e+ + 2ν
Actually the sun produces 4x1026 watts (one trillion times the power consumption of the human race!).
How many ν's?
2 ν's for every He produced, so about
10MeV/ν & 4x1026 watts ⇒ 1039 ν's/s ⇒ 9x1014 ν's m-2s-1
This gives 100 billion ν's pass through your thumbnail every second (You didn't notice?!?! Tsk, tsk!)
However, it takes 1 million years for the energy to get from the core of the sun to the surface. It takes the ν's 4 seconds!
|
 |
Don't you no, I'm a ν The weakest particle of nature in the zoo...Not by Flanders and Swann
Solar ν's are produced via (see John Bahcall)

| Note that all of them convert 1H into ⁴He, but the routes are different. These various processes have different energies. Probability of observing a ν α energy: i.e. only easy ones to see are 8B |  |
Detectors: Require a target which will give a suitable end-product when hit by a ν : e.g.
37Cl +ν ⇒ 37Ar + e-
37Ar is radioactive and decays after 35 days (back to Cl + e )
Rates: 1 SNU (solar neutrino unit) = 10-36 captures/atom/second
Expectation in 1961 20 SNU's, now 5 SNU's
| Davis expt (133 tonnes) of Cl (in the form of C₂Cl4: perchlorethylene). Find Ar atoms by flushing system with He, picks up Ar, then collect it and watch for decays
How many? 5 SNU implies 1 atom of 37Cl converted/day (a needle in a haystack?). Run for 3 months, search for Ar37 |
 |
Now results show 7.9 SNU's expected 2.1 observed.
Davis gets Nobel Prize 2003 (Bahcall, who did the calculations, should have done as well!)
Where have all the ν's gone?
Experimental error(?)
Obvious ones checked, but need totally new experiment
e.g. Kamioka
Astrophysics wrong(?)
e.g. B8 goes as T15: only need a small change (cooling) in center of sun to get rid of all of them.
e.g. sun older than thought
e.g. sun has gone out
Particle physics wrong(?)
e.g. ν's decay on way out
e.g. ν's turn into another kind of ν
| e.g. WIMPs (weakly interacting massive particles) transfer energy from core to outside region of sun very quickly
Need to be very odd particles: must be heavy (e.g. 50 x proton mass) with very small interaction X-section. σ. Aside:
X-sect is measured in barns = The typical nuclear diameter is of the order of 10−14 m. We might therefore expect the cross sections for nuclear reactions to be of the order of πr2 ≈1 barn =10−28 m2 e. g. Orbital period in core ≈ 10 mins |
Need totally new experiment (and M$60)
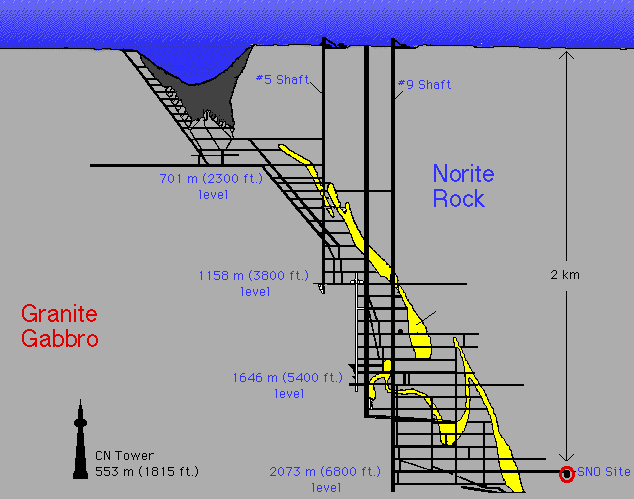
Sudbury Neutrino Observatory (SNO) How does this work? . Need to go deep to get away form cosmic rays  |
 SNO collaboration |
| in the Creighton mine (note the other bit of astronomy: the Sudbury basin is an old meteorite crater | 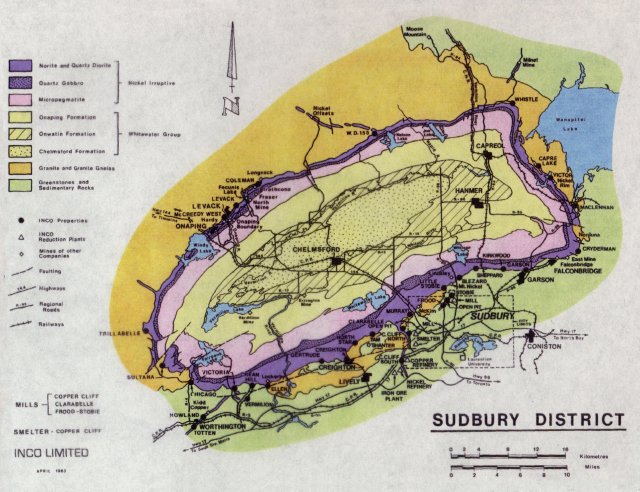 SNO collaboration |
SNO uses 1000 tons of D₂ ν + d ⇒ e- + p + pallows ν's to be seen immediately. |

|
| Must be pure (radioactivity gives false positives) < 10-15 parts Radium |  SNO collaboration |
| Light (photons) are picked up by photo-tubes |  SNO collaboration |
| 11000 look like this |  SNO collaboration |
| Produces "rings" of light which allow incident particle to be reconstructed |  |
Great advantage of SNO is that it can measure
ν e+ d ⇒ e- + p + p
ν x+ d ⇒ ν x + p + n
ν x+ e- ⇒ ν x + e-
CC = ν e NC ν e + ν μ + ν τ CC = ν e ES ν e + 0.15(ν μ + ν τ)allows simultaneous measurement of ν e and ν x
The ν'es produced in the sun change to another kind of ν on the way over.
Why? We don't know, but it means that ν's have mass.
The prob. of one kind of ν is given by
P = sin²(2θ) sin²(1.27 Δm²L/E)
One consequence: the amount of mass in the universe due to ν's is more than all the mass of the "ordinary" matter combined (and we'll worry about this later) Now need to understand explosive stars