Dark Matter

So how do we weigh the universe?

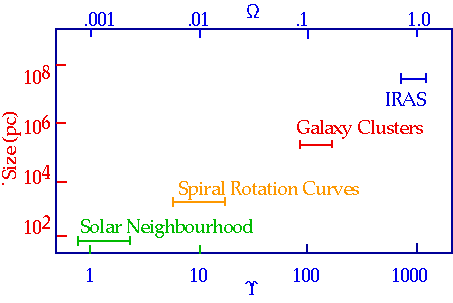
Can only see luminous matter: how much Dark Matter is there? Usually expressed as mass to luminosity ratio (Upsilon) Υ = M/L; For sun

Υ₀ = M₀/L₀ ≈ 5000 kg/W

First Guess: What you see is what you get!

• Count number of galaxies in a region of space, assume they consist of stars much like the sun, so Υ = M/L = M₀/L₀ Obviously must average over large enough volume such that universe is smooth R > 100 Mpc, and the universe is a very lumpy place!

• => Density:

  Ω = ρ ~ .005      
      ρ₀ 
  

• (Note all these numbers are uncertain to ∼ 50%!)
• We live forever!!!

1^st order estimate:

based on loose estimates of dark nebulae, obscuration of light and dust seen in other galaxies
\color{red}{ \frac{{\rho _{DM} }}{{\rho _{lum} }} \approx 1 \Rightarrow \frac{M}{L} \approx \frac{{2M_o }}{{L_o }}}
• Local Dynamics:Zwicky/Baade Can get estimate of local density by motion of stars
  \color{red}{ \frac{{\rho _{DM} }}{{\rho _{lum} }} \approx 2 \Rightarrow \frac{M}{L} \approx \frac{{3M_o }}{{L_o }}}
• (first direct evidence for D.M.)

Masses of Spiral galaxies

direct observation i.e. measurement of velocities of individual stars in nearby => rotation curves or measurement of hydrogen via 21cm line or estimates of no. of stars
Luminosity of galaxy should reflect mass

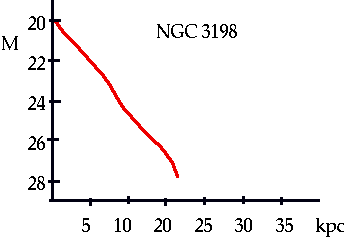Typical Spiral (NGC3198) R ≈ 20 kpc but outer parts are just seen as H gas

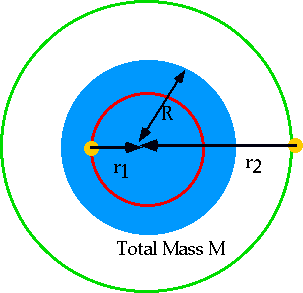
Should be able to calculate rotational speed In core of galaxy, mv²/r1 = G M(r1)m/r1² M(r1) is mass inside orbit: total mass M =⁴/3 πR³ ρ and M(r1) = ⁴/3 π r1³ ρ = M r1³/R³ Hence inside core: v²/r = G Mr³/(r²R³) or v = (GMr²/R³)1/2 Outside core: mv²/r = GMm/r² or v = (GM/r)1/2

Most of the light is fairly concentrated, so this should be good approx to the mass. These show rotation curves i.e. velocity curve doesn't drop as expected
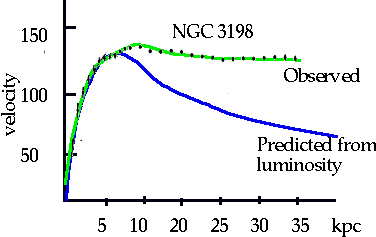Can fix this by saying that galaxy has halo of dark matter around it. Hence outside core but still inside halo force = force due to core + force due to halo v²/r = GM/r² + G M'r³/(r²R'³) or v = (GM/r + GM'r²/R'³)1/2

Not perfect: by fitting we can get a better result Halo + core add together to give correct curve

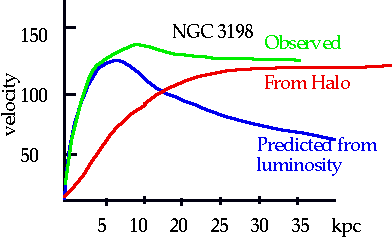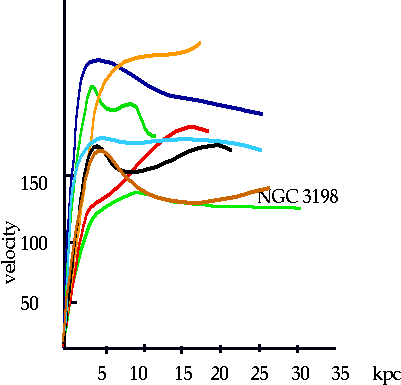
• Note this is not unique to NGC 3198: all measured spirals show same. (Have to have spiral that is not "flat on", since no Doppler, or "side on" since cannot separate different parts)

Implication: Mass of observed galaxy ≈ 10¹⁰ M₀, R ≈ 2 kpc (for core)
Mass of halo ≈ 10¹³M₀, R ≈ 100kpc (except that we can't measure out there!)

What do we mean by mass of galaxy? In fact the visible part of the galaxy may just reflect the dark matter.

Large clusters of galaxies:

<K.E.> = -1/2<P.E.> 

• \color{red}{ \frac{1}{2}M\left\langle {v^2 } \right\rangle = \frac{\alpha }{2}\frac{{GM^2 }}{{r_h }}}
• α = 3/5 if we just had a sphere: α ∼ .4 from small clusters
• r_h is radius that contains half the mass
• Just like measuring mass of a planet via orbits of its moons, except that
• 1. the mass isn't all concentrated at the centre
     
  2. can only measure velocity in one direction
     
  3. must assume that the peculiar velocities cancel out.

Radial vel. of individual galaxies given by \color{red}{ \left\langle {v^2 } \right\rangle = \left\langle {\left( {v_r - \left\langle {v_r } \right\rangle } \right)^2 } \right\rangle \sim 2x10^{12} } Roughly for Coma, rh ∼ 1.5 Mpc, so \color{red}{ M_{Coma} \approx 10^{15} M_ \odot ,L_{Coma} \approx 10^{13} L_ \odot }

This gives much higher masses than indivdual spirals

A check: Large clusters contain a lot of hot gas, which is strong X-ray source X-ray pictures measure density and temp:

• \color{red}{ \frac{{dP}}{{dr}} = - \frac{{Gm\left( r \right)\rho \left( r \right)}}{{r^2 }},P = \frac{{k\rho T}}{{\mu m}}}
• hence can measure m(r) which is the mass attracting the more distant gas

• M ≈ 1015 M₀  ⇒ Υ = 300Υ₀
  

  for Coma
• This gives much higher masses than individual spirals.

Also large clusters show gravitational lensing, can get quantitative estimate: Einstein ring (if lensing is perfect) \color{red}{ \theta _E = \left( {\frac{{4GM}}{{c^2 d}}\frac{{1 - x}}{x}} \right)} if distance is d and lensing object is at xd

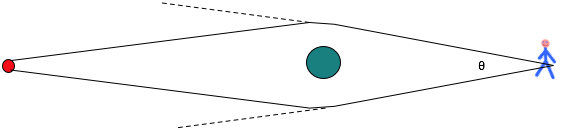• For Abell 2218 (z = .18) again M ≈ 1015 M₀ ⇒ Υ = 300Υ₀

Combination of lensing (blue) and X-rays (red) in the bullet cluster:

---

Strong evidence for non-interacting dark matter: X-ray emitting material is gas, so gets stopped in collision dark matter gets carried along

Note that the larger the object, the more massive (proportionately) that it is.

• a) What the hell? i.e. what is the dark matter?

• b) Why the hell? i.e. why is Ω~1 (after all it could be anything?)

• Actually, there is a limit \color{red}{\Omega < 3} , otherwise the universe would be younger than the earth (wouldn't that make the creationists happy!!)

  ---

  What the hell:

  1. Brown dwarfs
  2. Hydrogen gas
  3. Jupiters
  4. Hydrogen rain
  5. Low surface brightness galaxies
  6. Maxi Black holes
  7. Mini Black holes
  8. Neutrinos
  9. He H ⁺
  10. Modified 1/r² law
  11. Axions
  12. Weakly Interacting Massive Particles (WIMPS)
  13. Magnetic Monopoles
  14. Majorons
  15. Photinos
  16. E₈ shadow matter
  17. Cosmic Strings
  Which is it? We don't know! However, all of the above have problems.

  ---

  The Generic Candidates for Dark Matter :
  1. Baryonic (BDM) ordinary matter, but maybe in some odd form e.g. rocks
  2. Hot (HDM) particles which were relativistic at time of BB e.g. ν's
  3. Cold (CDM): heavy (usually) particles e.g. WIMPs
  4. Mixed (MDM) e.g. 70% WIMPs, 30% ν's
  5. Decaying Dark Matter (DDM)
  Why can't it be all BDM (wouldn't it be a lot easier?).

  We'll see later that primordial concentrations gave Ω_B ≈ .03--.1 (Much too low!!!)

  i.e. the dark matter cannot be all "normal" baryonic matter.

  ---

  MaCHOs

  Massive Compact Halo Objects: Brown dwarfs/Jupiters

  If Ω = .01 in luminous stars +BDM, would need 100 × mass in non-luminous objects to reach Ω = 1
  If mass = .01M₀ (high), we would need 10⁴ Brown Dwarves for every "normal" star, or 10⁵ Jupiters. Several brown dwarfs found

  We need to search for stars in IR (T ≈ 1000K) None in our neighbourhood.
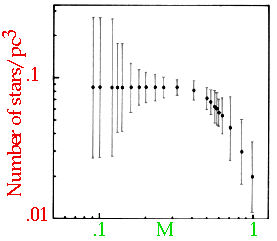  would need

  ---

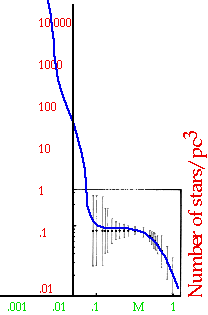  Microlensing

  If one star passes in front of another, we cannot see a double image (as with quasars), but we can see brightening as the BD passes across a star's image.

  The predicted rates are reasonable:

  MASS (M₀)	Radius (m)	Mean μ-lensing time	# Events/Month
  10	3 × 109	>1 yr	0.5
  1	109	3 mth	1.0
  10-2	108	9 d	5
  10-4	107	1 d	50
  10-6	106	2 hr	500
  10-8	105	12 min	5000

  ---

  Distinguishing them from variables: Must be symmetrical, achromatic, single, on-off events.

  ---

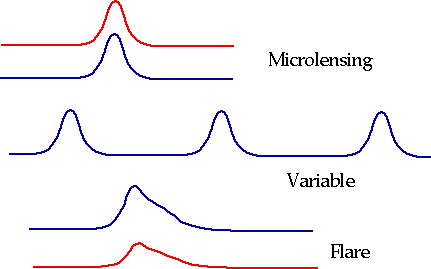  The Experiments

  Eros, ≈ 10⁶ stars.
  Macho, 300 digitized plates + CCD

  Experiment	Candidates	M	A	τ
  Eros	2	19.3	2.5	26 days
  Macho	1 good	19.3	3.3	30 days
  	+3 poor
  OGLE	4 poor			11->45 days

  ---

  • Macho 1 "Gold-plated" event M = 19.55 A = 6.8 τ ≈ 33.8 days

  • 
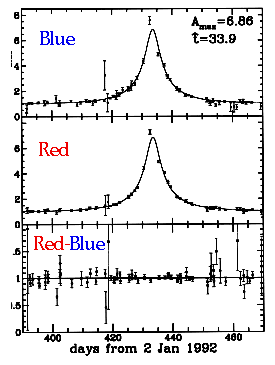
  • This event was also seen (but not completely) by EROS: Consistent with M = .1M₀ and with Ω ≈ .1 and with all of halo consisting of these.

  ---

  • Neutrinos: SNO showed us ν's must be massive. Since they were formed in the BB and are about as numerous as γ's, we'll come back to them later
  • Hydrogen gas: Can't see 21cm Line, so would have to be very diffuse (<.1 atom m^-3) which doesn't solve the problem

  • Hydrogen rain (Boiling point of H₂ is 22K)

  • Could exist in molecular clouds, but cannot explain clusters of galaxies.

  • Low surface brightness galaxies
  • Galaxies as big as (e.g. M31) but with only 10⁷ stars would be invisible. Number of these now known in local group

  • Not enough near us

  • Black holes, mini/maxi
  • Maxi: say 10⁸ M₀: Only occur in centre of galaxies (?). Created during active (quasar) stage of galaxies
  • Mini: M ≈ 1 M₀, Created during Big Bang Not made in large enough numbers (Hawking)

  ---

  No-Nameons: CDM candidates

  • • Axions
    • Majorons
    • Weakly Interacting Massive Particles
    • Photinos
    • LSP's (Lightest Supersymmetric Particles)
    • Magnetic Monopoles
    • E₈ shadow matter
  • ....and there is a tooth fairy

  • Although these are similar cosmologically, they are very different from the point of view of detection.

  ---

  Rates

  : Rate

  Particle interaction X-sect =σ ∼ 1-44m2 Velocity of WIMP wrt earth = vW (∼ 600 km s-1) so energy \color{red}{E = \frac{1}{2}M_W v_W^2 } WIMP Density: naively: \color{red}{{\rm{n}}_{\rm{W}} {\rm{ = }}\frac{{\Omega _M \rho }}{{M_W }}} However, if we use the halo density (instead of mean density) we can get \color{red}{ \rho _{halo} \approx 10^6 \rho _0 \approx 10^{ - 20} kgm^{ - 3} }

  • Assume an elastic colliion with nucleus: Energy transferred to nuc recoil \color{red}{E = \frac{1}{2}M_N \left( {2v_W^{} } \right)^2 \sim 20keV}
  • If we have N_T target nuclei, rate is \color{red}{R \approx N_T {\rm{n}}_{\rm{W}} v_w \sigma } Plausible to expect that the local WIMP density is much higher than ρ_c, so rates can be few/day

  ---

  A lot can be ruled out by "in vitro" experiments

  • e.g. OPAL (Richard Hemingway and others) at CERN puts limits on LSP's and any WIMP with standard weak interaction X-sects.

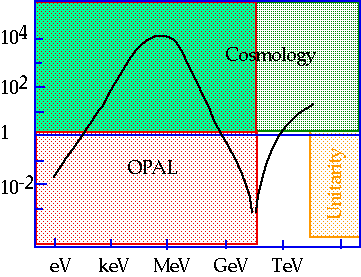  • ATLAS will be able to rule out a lot more options (any reasonable with m < ∼ 1TeV)
  • or of course discover it!

  ---

  Generic WIMPS can be seen "in vivo" via a variety of low temp. expts.:

  In solid, nucleus will recoil and transfer energy to lattice, flipping superconductor or sending off ballistic phonons. So far, no results!

  ---

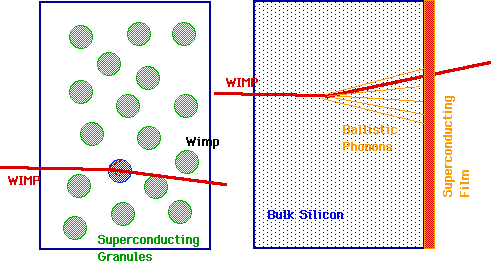  e.g. Queens-U de Montreal Picasso expt. Nucleus will recoil and transfer energy to super-heated freon liquid and cause transition to gas.

  ---

  • DEAP (see Kevin Graham): will use 1 tonne of liquid argon: can set useful limits

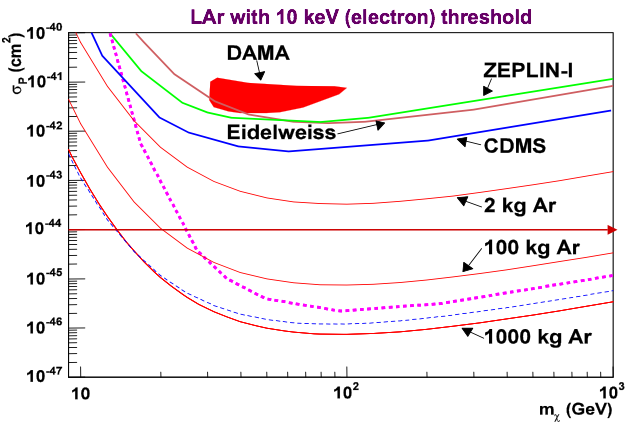  • Can also set limits from other astrophysical arguments
    • can't cool stars to quickly
    • WIMPS will annihilate at galactic centre giving γ's
    • could annihilate in sun giving high-energy ν's
  • Collect your Nobel prize on the way out........

  ---

  What the hell:

  • Brown dwarfs Not enough
  • Hydrogen gas Would be seen unless it was very diffuse, in which case, not enough
  • Jupiters Not enough
  • Hydrogen rain Too hot
  • Low surface brightness galaxies Doesn't fix the problems in spirals
  • Maxi Black holes Only exist at the centre of galaxies: we need halos
  • Mini Black holes Not enough
  • Neutrinos Part of the solution, but too light to create structure
  • He H ⁺ Unstable
  • Modified 1/r² law Hard to reconcile with Bullet cluster
  • Axions Negative searches so far
  • E₈ shadow matter and there is a tooth fairy...
  • Cosmic StringsForm in wrong place
  • Magnetic Monopoles Screw up magnetic fields in galaxy
  • Weakly Interacting Massive Particles (WIMPS)
  • e.g. Photinos Will see them in 2008 (maybe)
  • Now want to look at the next major ingredient: the microwave background