CMBR

WMAP

Cosmic Microwave Background Radiation

Early universe must have been very simple: there can have been no stars or galaxies. However, it was very hot: hot things radiate....

Universe is "full" of light: fossil light from Big Bang, discovered accidentally by Penzias and Wilson (1964)

Found that "noise" came from universe independent of what angle horn was pointed in: corresponded to a black-body temp of 3⁰K

Have to get above atmosphere and point away from Milky Way.

Have to get above atmosphere and point away from Milky Way

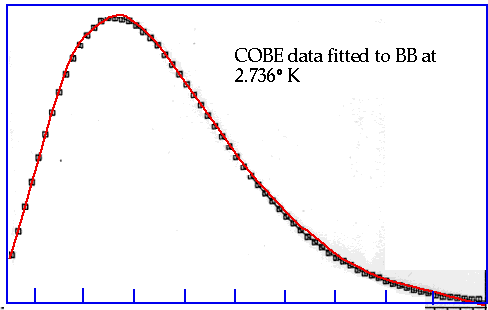
Subsequent values came from balloon flights:

Finally COBE launched 1990:

Note the perfect Black Body curve.

Where does it come from?

Gamow (1948) discussed Hot Big Bang for first time, suggested that E.M radiation from it should still be observable. Peebles (1964) had calculated that it should be observable, but thought T ~ 10 ⁰K, (and everyone had general feeling that it would be unobservable).
This "light" is now at 2.736°K, and almost uniform in every direction. It was emitted just 500000 years after the Big Bang and has been travelling round the universe ever since. At time t₀, the universe is full of γ's at a temperature T₀.
More exactly: from the Black Body equation:
Energy density:
```
u = T⁴ × ⁸/₁₅π⁵k⁴/(h³c³) = aT⁴ = 4σT⁴/c
```
(Stef.-Boltz.) Photon density N ≈ 20 x 10⁶ T³ m^-3
Mean γ-energy E ≈ 2 x 10^-4 T eV actually = hc/λ = 6.58x10^-16 x 3x10⁸ /λ
Peak of BB curve is at λ = 2.898x10^-3/T
Now, the peak is at 1.05 mm: what is the temperature, N, E, ρ?

If we have only radiation $$ \color{red}{ \epsilon = \frac{{4\sigma T^4 }}{{c^3 }}} $$

which gives an exact expression for the temp: $$ \color{red}{ T^2 = \frac{1}{t}\sqrt {\frac{{3c^3 }}{{64\pi G\sigma }}} ,t = \frac{\xi }{{T^2 }}} $$

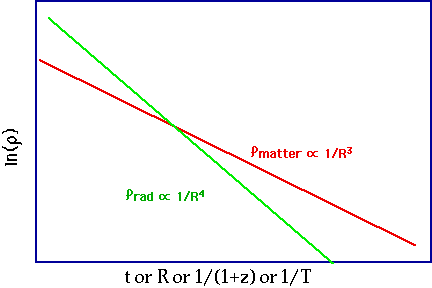
When did the universe stop being radiation dominated?

Need the R dependence of energy density, ρ and the current ratio of photons to baryons \color{red}{\eta = \frac{{n_b }}{{n_\gamma }} \approx 5 \times 10^{ - 10} }

suppose all the matter was non-relativistic(e.g. Baryons): Relativistic particles (i.e. γ's, ν's) get red-shifted as well, so

\color{red}{\begin{array}{l} \varepsilon _m = \frac{{\varepsilon _{m,0} }}{{a^3 }},\varepsilon _{m,0} = 9400 \\ \varepsilon _r = \frac{{\varepsilon _{r,0} }}{{a^4 }},\varepsilon _{r,0} = .26 \\ \end{array}}

We live in matter dominated universe

ρ_matter >> ρ_rad,

but it was not always thus

So these were equal when: \color{red}{\frac{{a\left( t \right)}}{{a\left( {t_0 } \right)}} = \frac{{\varepsilon _{r,0} }}{{\varepsilon _{m,0} }} \approx \frac{1}{{3600}}}

Photon freezeout:

Thermal equilibrium between matter and radiation implies they are at the same mean energy, with a Black Body distribution of γ's. Expansion ⇒ Cooling.
The universe was originally opaque (i.e. mean free path of γ's very small) and hence CMBR was in thermal equilibrium with matter. Then the universe "condensed" (or froze) out.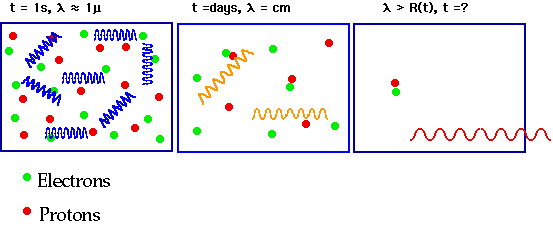
As the peak in the BB curve falls below hydrogen binding energy, ¹H forms, at ~3700 K, ie about ¹/₂eV. When did this happen?
(Note, this is less than the 13.6 eV that you would expect: need Saha equation)
When was the temp 3700K?.
```
τ ≈ ζ/T² ≈ 500,000 yrs, or 1+z ≈  T/T₀ ≈ 3700/2.736 ≈ 1360
```
i.e, at about the same time that the universe became matter-dominated.
(Note: we began with a very large uncertainty, setting Ω ≈ 0.01, based on .03 proton per cubic metre: depending on the nature of the DM we can change this by a factor of 10)

COBE/WMAP results

COsmic Background Explorer
Wilkinson Microwave Anisotropy Probe
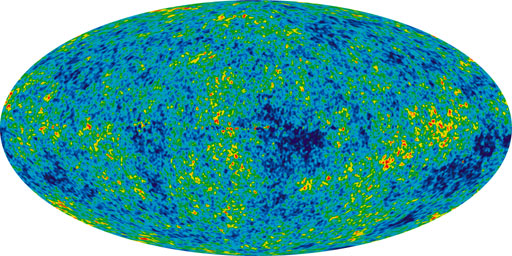
Temp. of the microwave sky in a scale in which blue is 0 K and red is 4 K. Note completely uniform on this scale. The actual temperature of the cosmic microwave background is 2.725 Kelvin.

WMAP measures at 5 wavelengths: longest wavelengths are most affected by galaxy

Dipole effect: if we are moving through CMBR we would expect to see it "warmer" in front and "colder" behind.

Blue ↔2.721 Kelvin
red ↔2.729 Kelvin

so CMBR is blue-shifted in the direction we are going in (note residual effect of galaxy): what do we expect for 600 km/s?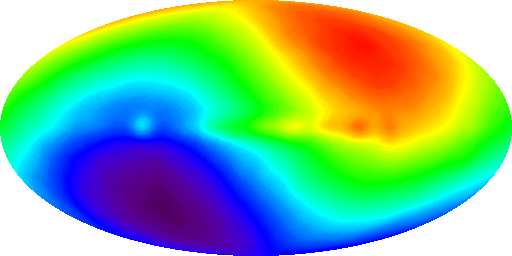

Credit: DMR, COBE, NASA, Four-Year Sky Map

Except there is a tiny problem: some of the features in the CMBR seem to be aligned with the solar system....

shows we are moving towards Leo at≈ 606 km/s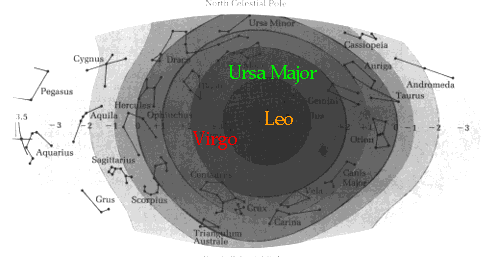

Quantatively:

Can just see structure at: ΔT/T ≈ 10^-6: Indicates that the universe was very uniform back then. hotter where it is denser, and this shows where the galaxies should be forming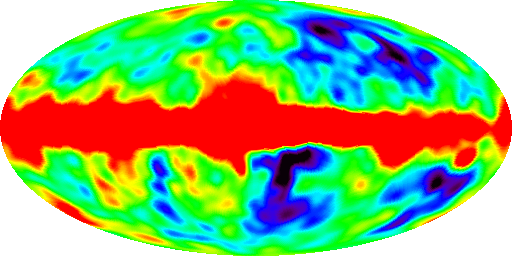

>What size fluctuations do we expect?

\color{red}{ \left\langle {\frac{{\delta T}}{T}} \right\rangle = \left\langle {\frac{{T - \left\langle T \right\rangle }}{{\left\langle T \right\rangle }}} \right\rangle = 1.1 \times 10^{ - 5} }

Temperature Fluctuations:

Well formed galaxies were there at z ≈ 1, t ≈ 3 ×10⁹ years
New observations suggest they are there at z ≈ 4.: Lyman forest shows hydrogen clouds present very early

How did the galaxies form so quickly between t ≈ t_dec (where there are no indications)
and
t ≈ 2 × 10⁹ years (where they are well formed and look like today's galaxies)?

Seeds must have been there ⇒ temp fluctuations.

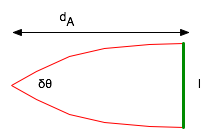
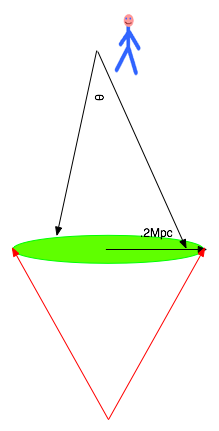
Angular size related to distance via δ θ

\color{red}{ \delta \theta = \frac{l}{{d_A }}}

COBE had angular resolution δθ = 7°
WMAP has δθ = 10"
COBE and WMAP comparison

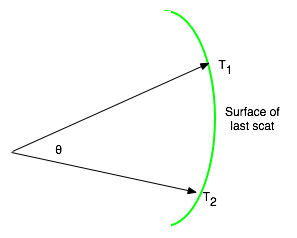
Hence can relate actual size of fluctuation at last scat. to angular size

\color{red}{ l \approx .22\left( {\frac{{\delta \theta }}{{1^0 }}} \right)Mpc}

Want to find correlation between temp at different points in the sky

\color{red}{ C\left( \theta \right) = \left\langle {\frac{{\delta T_1 }}{T}\frac{{\delta T_2 }}{T}} \right\rangle _{\cos \left( \theta \right)} }

Can make Legendre polyn expansion:

\color{red}{ C\left( \theta \right) = \frac{1}{{2\pi }}\sum\limits_{}^{} {\left( {2l + 1} \right)} c_l P_l \left( {\cos \left( \theta \right)} \right)}

(usual expansion in orthog functions, so quite general). Actual map has no importance, but info about early universe is in multipole moment c_l: large l corresponds to small ang. separation in sky.

Cause:

At t_ls, Hubble distance d_H= c/H(z)= ∼ .2 Mpc.

Any fluctuations smaller than Hubble distance could be correlated
Any larger ones must have a different cause
corresponds to angular size now θ_H ∼ 1° or l ∼ 200
Hence importance of ang. res.

Source: Fluctuations in energy density ⇒ changes in grav. potential ⇒ grav red-shift (Sachs-Wolf effe3ct)

\color{red}{ \varepsilon \left( r \right) = \bar \varepsilon + \delta \varepsilon \left( r \right) \Rightarrow \nabla ^2 \left( {\delta \phi } \right) = 4\pi G\delta \rho \left( r \right) \Rightarrow \frac{{\delta T}}{T} = \frac{{\delta \phi }}{{3c^2 }}}

COBE/BOOMERANG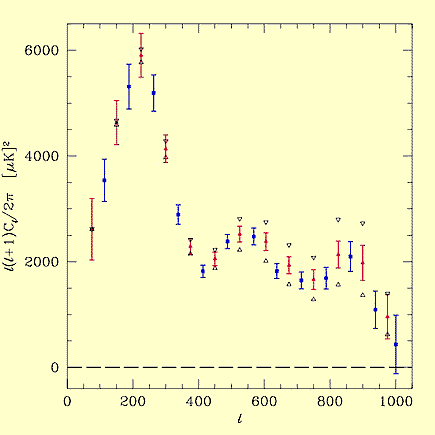

WMAP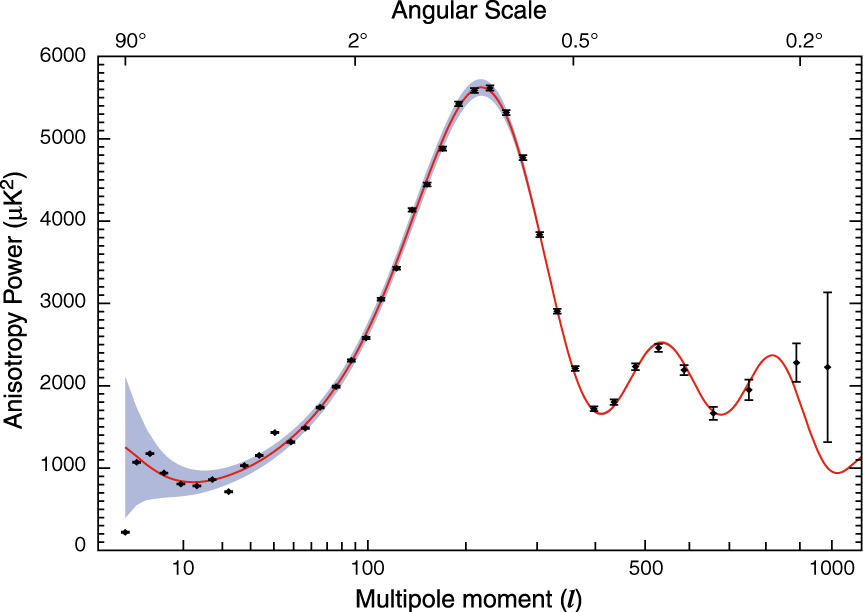

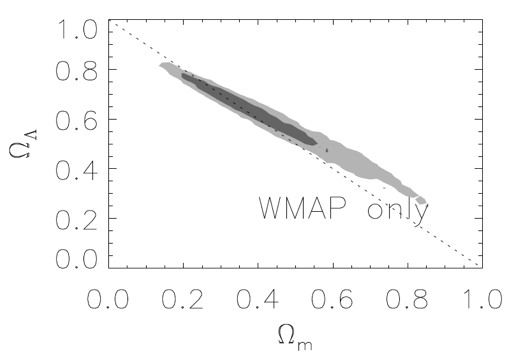
i.e. measuring temp differences gives us direct measurement of density fluctuations.

High density ⇔ High δT
Also, because of dependence of angular size on geometry, the multipole plot gives direct measurement of curvature

:
Structure looks smaller, peak shifts to larger l > 180 if universe has κ = -1.
Structure looks larger, peak shifts to smaller l < 180 if universe has κ = +1.

Small-scale fluctuations

Highest peak at l = 180 corresponds to Hubble size at the time.

Before decoupling, Universe is filled with photon-baryon fluid.
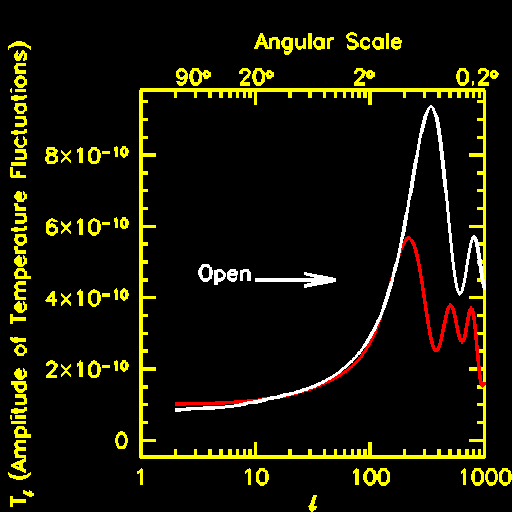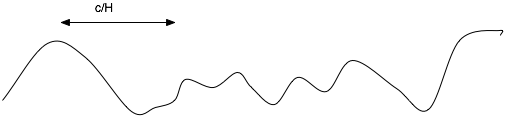
Normally density fluctuations die away (e.g sound waves) but in massive fluid they get amplified by gravity

\color{red}{ P = w\varepsilon } with w = 1/3 for photons, w = 0 for matter so 0<w_pb<1/3.
will give acoustic oscillations : speed of sound
\color{red}{ v = \sqrt {\frac{{dP}}{{d\rho }}} = \sqrt {\frac{{c^2 dP}}{{d\varepsilon }}} = c\sqrt {w_{pb} } }
(i.e. in a pure γ or ν gas, v = .58c)

Except that we have a self-gravitating fluid:
fluctuations will cause higher density, and will attract fluid:
if it gets too dense, pressure will drive it apart.

Different models for gas: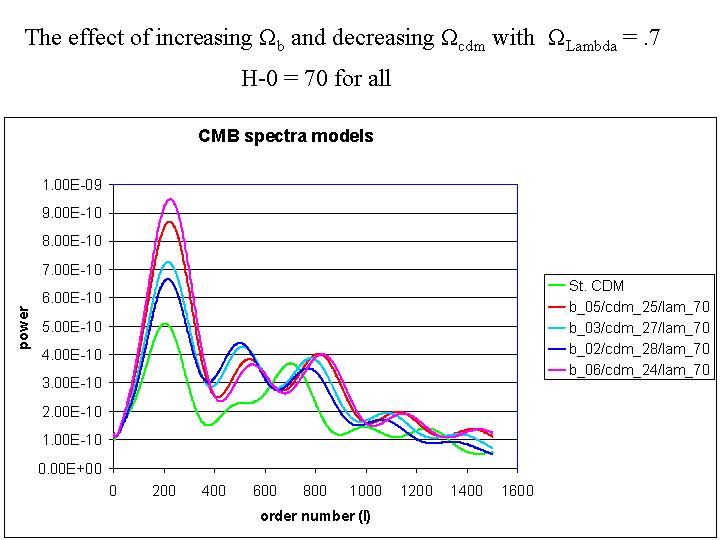

Consistent with κ=0 and Ω₀=1
Ω_b∼ .04
⇒ Benchmark Model
Will add info from supernova later

Now need to look at very early universe