4201 Telescopes

Advanced Technology Solar Telescope (ATST)

Lenses

There are a variety of lens, but essentially they are converging (usually convex) diverging (usually concave)

• Convex lenses create a real image (i.e. one that can be cast on a screen)

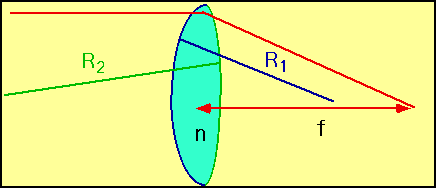
  The most important quantity for a lens is the focal length f: i.e. how far from the lens do parallel rays get focussed.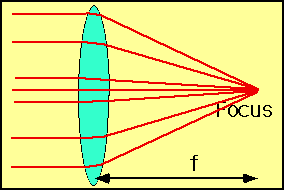

• Rules for "ray-tracing" diagrams:
• a ray which goes through the centre of the lens is not deflected.
• a ray that is parallel to the axis must go through the focus.
• a ray that goes through a focus must go parallel to the axis.

The thin lens equation

• \color{red}{ \frac{1}{f} = \frac{1}{{d_0 }} + \frac{1}{{d_i }}}
• The surprising thing about this formula is that it always works provided we remember certain conventions:
• real objects have d_o > 0
• real images have d_i> 0
• virtual ones have d_i < 0
• objects above the axis have h_o > 0
• images below the axis have h_i < 0
• convex lenses have f > 0
• concave lenses have f <0
• convex mirrors have f < 0
• concave mirrors have f >0
• mirrors have real images on the same side as the object
• lenses must be "thin": the approx. that is used is sin(θ)= θ

The lens-maker's equation:

\color{red}{ \frac{1}{f} = \left( {n - 1} \right)\left( {\frac{1}{{R_1 }} + \frac{1}{{R_2 }}} \right)}

• applies if the lens is "thin" (means that all angles are small enough so that θ = sin(θ))
• R₁,R₂ are the radii of curvature of the lens surface:
• convex surfaces have positive curvature,

Concave Mirror

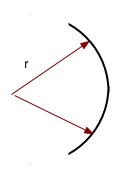
\color{red}{ f = \frac{R}{2}} because if you place a source at the centre the light must be reflected back there. \color{red}{ \frac{1}{f} = \frac{1}{R} + \frac{1}{R}}

• Image is real and inverted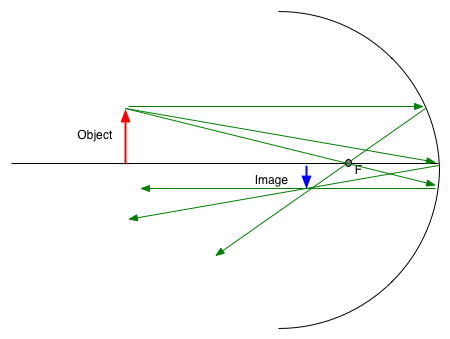

Compound systems

• Draw a diagram (!) with object and a guess at the light-path
• Find out where the first lens produces an image
• Use this image as the object for the second lens (if the object distance is negative, it means that it is just a virtual object)
• Find out where the final image is. We can simulate lens systems on an optical bench

Young's slits

is this interference experiment done for light.

• Distance between sources is small (d) Distance to detector is large (D) so waves can be treated as plane waves, giving constructive interference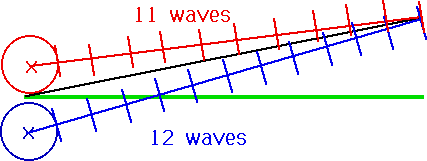

• If we have an extra ½ λ, will get destructive interference.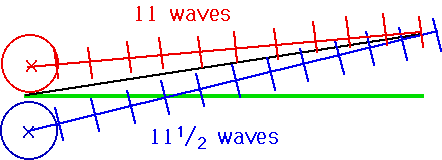

• 
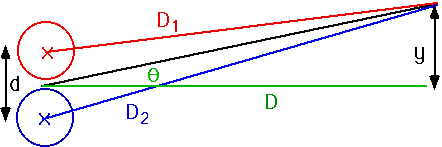
• Must have D₁ - D₂ = nλ for constructive interference n = 0,±1,±2,±3.....................
• We can derive

  \color{red}{\theta = \frac{{n\lambda }}{d}}

• For water waves, this can be done by two sources. For light, there is an extra problem: sources don't stay in phase...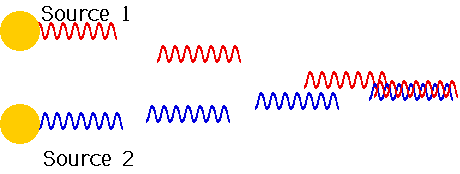

Geometry:

• \color{red}{\lambda = d\sin \left( \theta \right)} (note small angle approx can't be used here) so if white light is incident on diff. grating, it will be split up into constituent wavelengths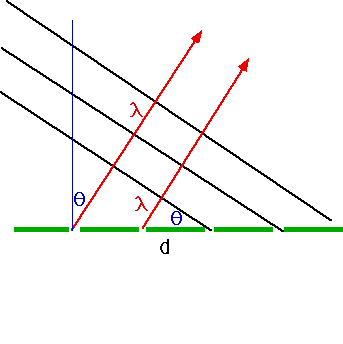

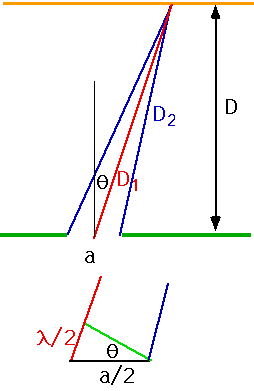
Single Slit

• Geometry

  To have destructive interference between light from centre and edges, need \color{red}{ D_1 - D_2 = \frac{\lambda }{2}} difference in paths

• i.e.
  \color{red}{ \sin \left( \theta \right) = \frac{{\lambda /2}}{{a/2}} = \frac{\lambda }{a}}

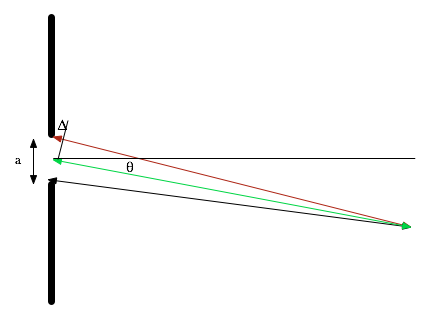
• Done properly: need Huyghens principle Field is \color{red}{ dE = \frac{{E_L }}{r}e^{i\left( {kr - \omega t} \right)} ds}

• Path difference \color{red}{r = r_0 + \Delta ,\Delta = a\sin \left( \theta \right)} so total electric field
  \color{red}{ E = \int_{ - \frac{a}{2}}^{\frac{a}{2}} {dE} = \frac{{E_L a}}{{r_0 }}\frac{{\sin \left( \beta \right)}}{\beta }e^{i\left( {kr_0 - \omega t} \right)} ,\beta = \frac{1}{2}kb\sin \left( \theta \right)}
• This gives us the intensity (actually irradiance)
  \color{red}{ I = I_0 \left| {\frac{{\sin \left( \beta \right)}}{\beta }} \right|^2 ,\beta \approx \frac{{\pi a}}{\lambda }\theta }
  "Fourier transform of the slit"

The intensity falls of very rapidly away from the centre line.

• Minima are given by
  \color{red}{ \sin \left( \theta \right) = \frac{{m\lambda }}{a},m = 1,2,3...}
• Centre (bright) is given by m=0
• Maxima are given by
  \color{red}{ \sin \left( \theta \right) = \frac{{\left( {m + \frac{1}{2}} \right)\lambda }}{a},m = 1,2,3...}
• note that two slit case is always almost always idealised to infinitely narrow slits

Telescopes have round(!) objectives

• Means that a point will be spread out into a disk, and hence the image of two close objects will overlap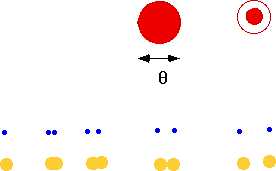

• Stars closer than this cannot be resolved into pairs.
• Implication: want (say)
  \color{red}{ \theta < 1'' \Rightarrow D > 2.52 \times 10^5 \lambda }
  Implies
  • D ~ 100m for radio waves
  • D ~ 10 cm for optical
  • Not relevant for X-ray or γ

Thin Film interference

• e.g. a wedge:

• if the light from the bottom level travels λ/2 further, there will be destructive interference between the two reflections. Since the path will depend on the separation, there will be a pattern of lines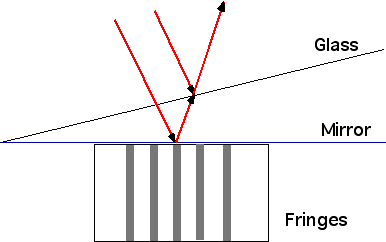

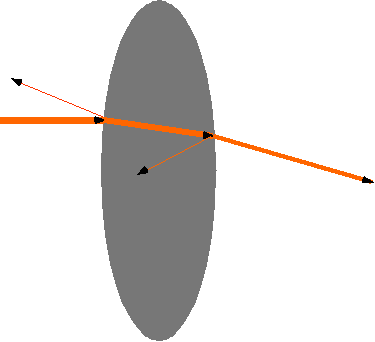
We can use this constructively to reduce the reflection from lenses: e.g. a surface will reflect \color{red}{ I_R = \frac{{n^2 - 1}}{{n^2 + 1}}I_0 }

• By coating the lens, we can arrange for destructive interference in the reflected wave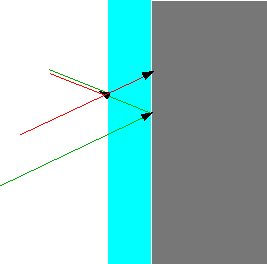

Dispersion

• Glass has (slightly) different refractive indices n for different λ, Hence a prism can be used to produce a spectrum.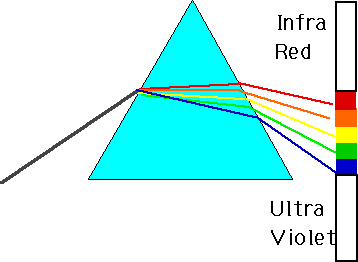

• Note that this mechanism is quite different from a diffraction grating (where different wavelengths interfere constructively at different angles).
• With a prism, the red light is deviated least (i.e. the velocity is largest), whereas for a grating it is deviated most.

• Thin lens formula assumes that deflections are small (i.e. sin(θ) = θ)
• In practice, light from outer region of lens is more strongly focussed than central part

• Effect is blurred image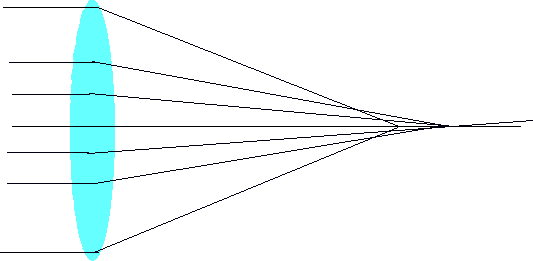

• One solution is to eliminate light from outside of lens by stopping down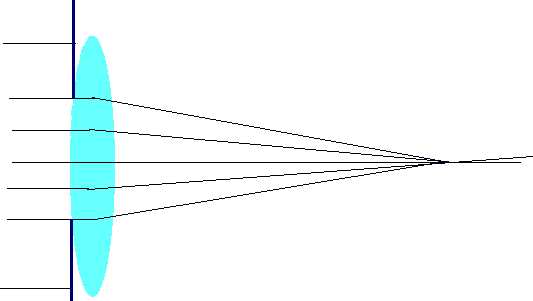

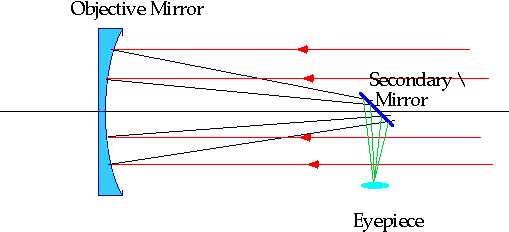
• Unfortunately this reduces the area, so you get less light. Only real way out is to go to non-spherical lenses/mirrors. e.g. for a telescope, spherical mirror gives blurred image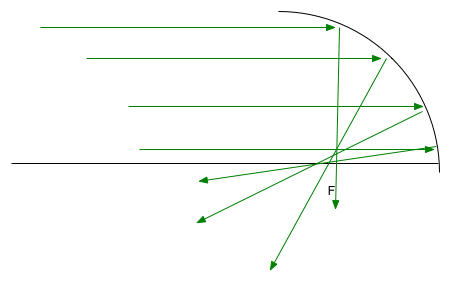

• Can be corrected by going to a parabolic mirror (but this only works for objects at infinity)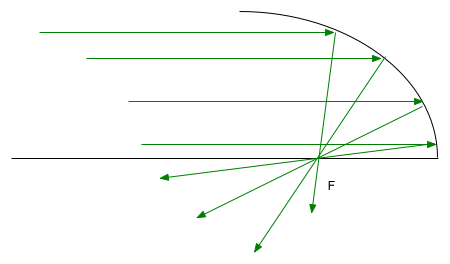

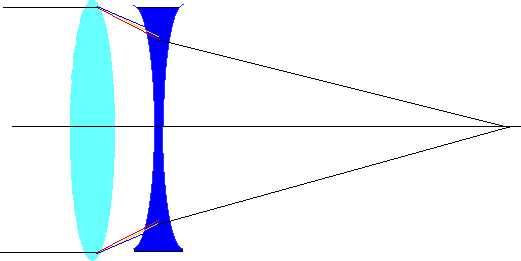
Chromatic aberration:

• Glass disperses light into constituent wavelengths, so get different foci for different wavelengths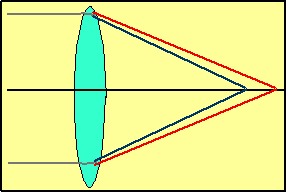

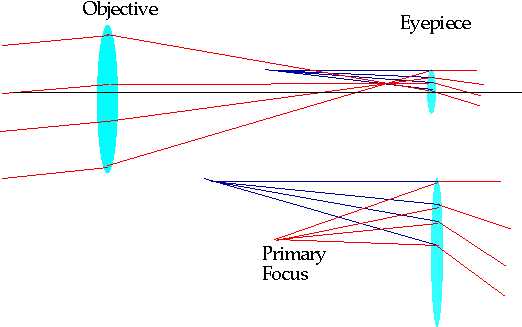
• Overcome by exploiting different dispersive powers of different glasses (usually "crown" and "flint" glass)
• In fact, objective is usually sandwich of several different glasses

Telescopes

• Simplest is two lens refractor. Objective is large lens at "front", brings light to a primary focus. Eyepiece is used to magnify image. Magnification: if f₀ is focal length of objective f₁ is focal length of objective \color{red}{ M = \frac{{f_o }}{{f_e }}}

• e.g. typical (cheap!) telescope objective might be f₀ = 150 cm, eyepiece .75 cm
• Problems:
  • Structural (need to support lens round edge) ⇒ Distortion
  • Chromatic Aberration
  • Spherical Aberration
  • Coma (Images at large angles to axis are distorted)
  • Twinkle (atmospheric distortions of star)

Brightness

• Want to collect as many photons as possible: " light bucket". Light-Collecting power ∝ area of objective: i.e. want to maximize R

• But also want image to show maximum image intensity Ii: If we have a finite sized object, then (Height) area of image will be ∝ (f) f2. Hence "figure of merit" in comparing two telescopes will be focal ratio \color{red}{ F = \frac{f}{D}} Want this to be as small as possible: good camera lens will have F ~ 2. Illumination \color{red}{ J \propto \frac{1}{{F^2 }}}

  ---

  Best refractors have D ~ 1m

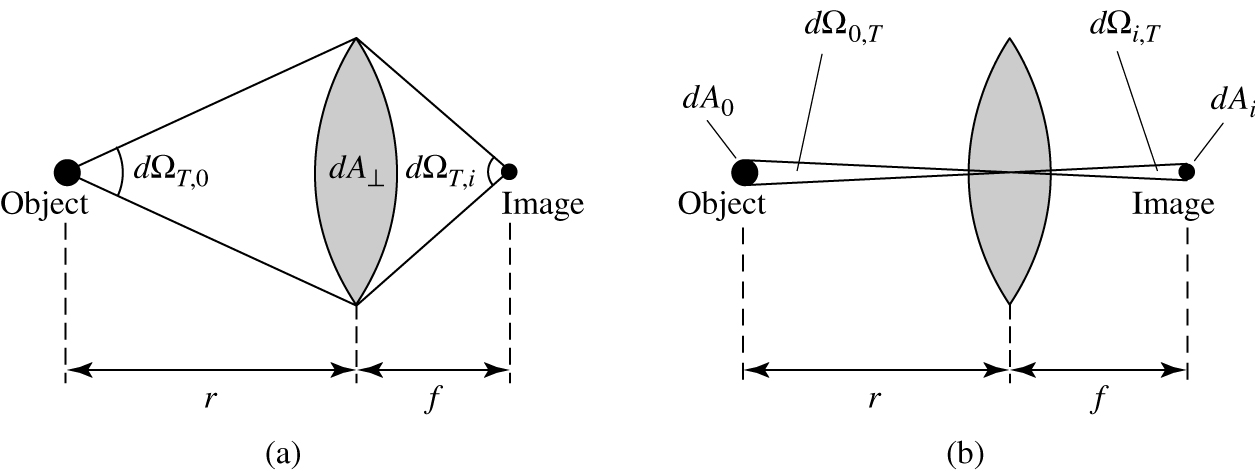
  • Newtonian reflectors Replace objective lens by mirror: Advantages: No chromatic aberration Support for whole of mirror Only one surface matters

  • Disadvantage: Spherical Aberration remains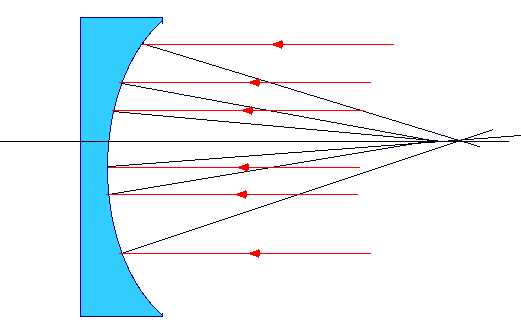

  ---

  Also need support for secondary mirror ⇒ diffraction "star"

  An Extraordinary Spiral from LL Pegasi

  Credit: ESA, Hubble, R. Sahai (JPL), NASA

  ---

  • "Best" standard telescope is Schmidt- Cassegrain Corrector plate is very weak aspherical lens to exactly (well, almost) compensate for spherical abberation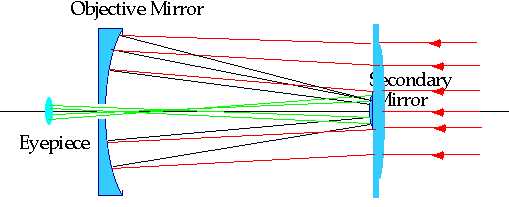

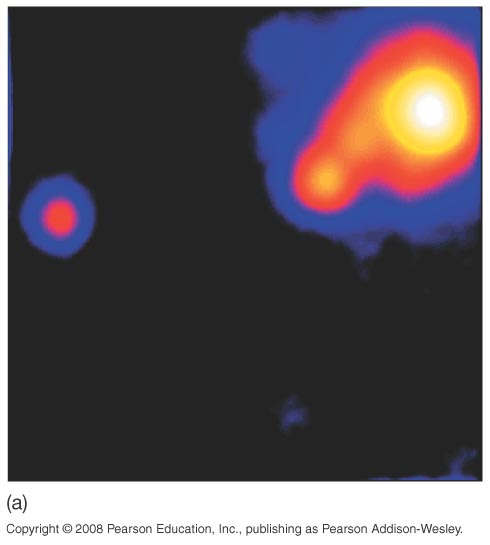
  • Gives compact design, with folded light-path, eyepiece at end, wide field of view. This is (essentially) what is used in the Hubble space telescope

  ---

  A spectacular picture from the Hubble: large masses can bend light,

  • so a very large cluster of galaxies (about 1013 MSun) can act as a (lousy!) lens. This cluster is producing multiple images of a much more distant galaxy.

  ---

  Adaptive Optics

  Atmosphere is unsteady. If we can measure the movement, we can make small adjustments to one or more of the mirrors to compensate

  Adjust position of pads several times per second to keep 'artificial star' aligned

  ---

  

Radio

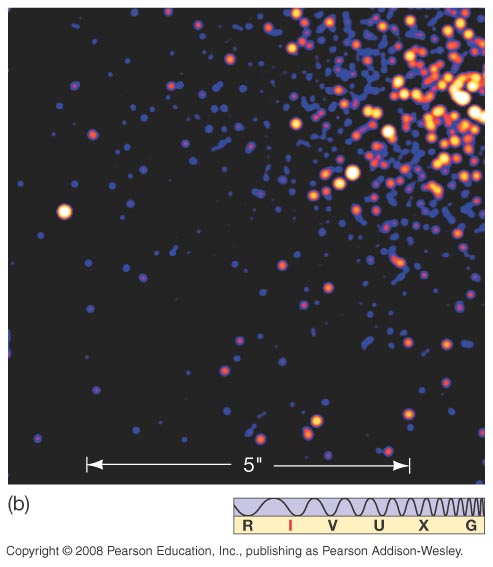
λ	E	Detection:	Absorption:	Observatories	Production:
∼ 1cm ↔ 100 km		Radio-receivers (masers for highest sensitivity)	Longer waves absorbed by atmosphere	Sea-level	Sun, Jupiter, few stars, pulsars, cold hydrogen (21cm), galactic nuclei
Need lots of collecting area but also high resolution ⇒ Large dishes (Arecibo), many hooked together (VLA)		A Very Large Array of Radio Telescopes Credit: NRAO, NSF

Infra-Red:

Canada-France-Hawaii Telscope (on Mauna Kea)

Visible

λ	E	Detection:	Absorption:	Observatories	Production:
∼ 400 nm ↔ 800 nm	∼ 2 eV	Eye, photograhic film, photoelectric detectors	Clouds	Sea level	Everything except cold matter
High, dry observatories (to avoid twinkle)		The VLT Interferometric Array Credit & Copyright: European Southern Observatory

Ultra-Violet:

X-rays

λ	E	Detection:	Absorption:	Observatories	Production:
∼ 10-12 m↔10-10 m	∼ 1 MeV ↔1 keV	Photograhic film, photoelectric detectors, photomultpliers	High	satellite	Highly excited atoms: T > 105 K
must get above atmosphere (Einstein, Chandra, XMM satellites)		XMM Launched Drawing Credit: D. Ducros, XMM Team, ESA

Can't be focussed or reflected: need to use grazing incidence mirrors

γ-rays:

λ	E	Detection:	Absorption:	Observatories	Production:
< 10-12 m	∼ 1 MeV ↔1018eV	Spark chambers, Cherenkov radiation in atmosphere	High	Satellite or upper atmosphere	Compact objects (e.g. black holes, neutron stars, supernovae)
can use the atmosphere as a detector		HESS Gamma-Ray Telescope Credit: The HESS Collaboration

Hubble

and above all, the Hubble which sees in the UV and IR and is above everything!

The Orbiting Hubble Space Telscope Credit: STS-103, STScI, ESA, NASA

These give us 70 octaves!

New telescopes

GMT: Great Magellan Telescope

• $0.6B, operational 2016 , ~50 yr. operating life

• 25.2m 7 segment primary mirror

• Candidate location Cerros Las Campanas, Northern Chile
• Spectral range λ = 0.32 μm to 25 μm (visible to near-IR)
• Initial key projects are:
  • Exo-planets and debris disks, 0.5 to 5 AU stellar regions, of stars with known exo-planets
  • Star formation, GMT near-IR synergy with ALMA in radio λ
  • Stellar populations, black hole growth
  • galaxy formation, synergy with JWST in IR

TMT: Thirty Meter Telescope

• $0.8B, operational 2017, Ritchey-Chretien design

• ~30m primary mirror, 492 hexagonal segments each 1.4 m dia.
• 2 candidate sites: Atacama & Mauna Kea
• Spectral range λ = 0.31 to 28 μm

European Extremely Large Telescope

• $1B USD, operational 2017

• ~42m primary mirror, consisting of 906 x 1.4 segments, adaptive optical control

• Top site candidate: Dome C, Antarctica;
• Spectral range λ = 0.45 μm to 20 μm
• Three broad main project objectives
  • search and characterization of exo-planets and
  • proto-planetary systems
  • formation and evolution of the large scale
  • structure of our universe from the 1st light to present day
  • testing the frontiers of physics (strong gravity, variations of fundamental constants, structure of space-time, etc.)

Space

L2 is preferred place: min of PE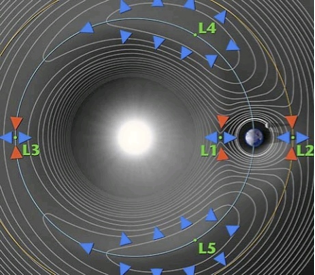

Full range of space observatories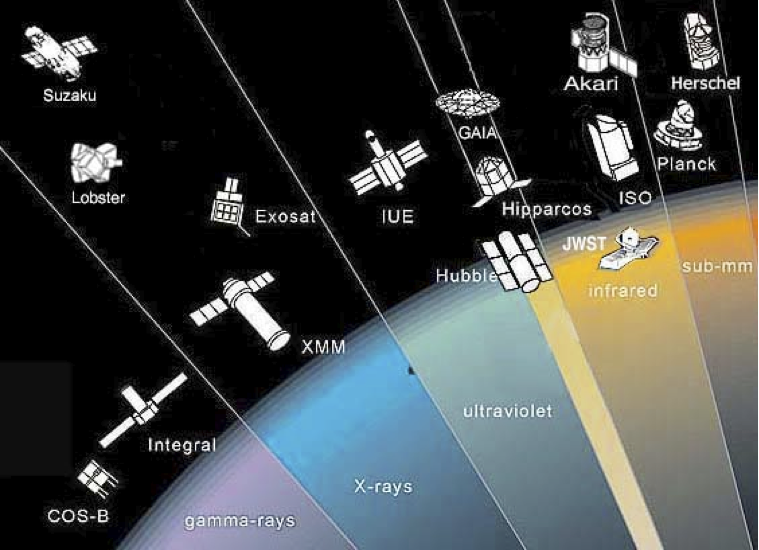

James Webb Space Telescope

6m primary (Hubble was 2.8m)

• Now we take a look at nuclear physics