
- Predict the behaviour of compound lens systems
- Understand the eye
- Understand telescopes
- Understand microscopes
- Explain the limitations of optical instruments
 |
Objectives: by the end of this you will be able to
|
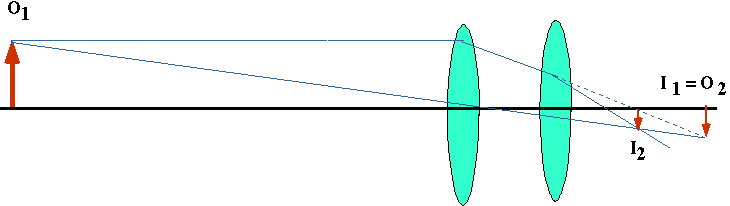
e.g. Two convex lenses, f = 10 cm for both are separated by 8 cm. If there is an object 10 cm high at 40 cm,
|
 |
| Works differently from any other optical instrument (such as camera, telescope..) in that focussing is performed by deforming the lens by the eye muscles. Means that eye can be focussed (ideally) from a far point of ∞ down to a near point of 25 cm. | 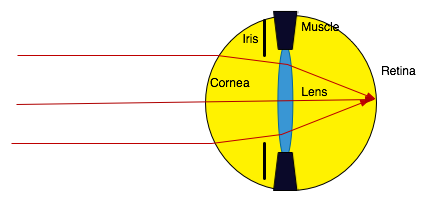
|
| Short-sight/Near-sightedness/myopia: caused by too strong a lens, corrected by concave lens. | 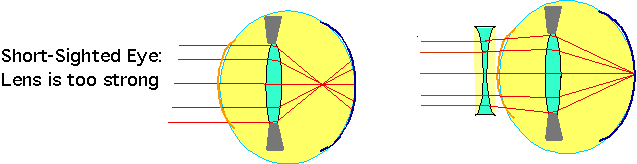 |
| Long-sight/far-sightedness/hyperopia: caused by too weak a lens, corrected by convex lens | 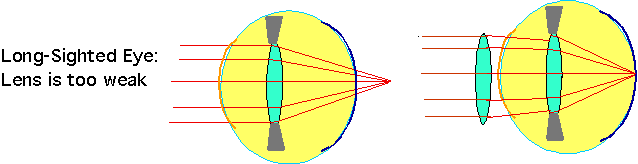 |
| The object is inside the focal length. e.g. the object is 2 mm high, f = 5 cm, s = 4.8 cm | 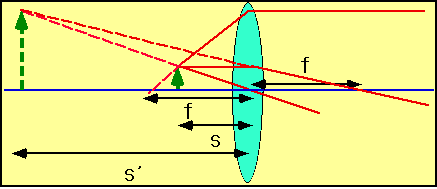
|
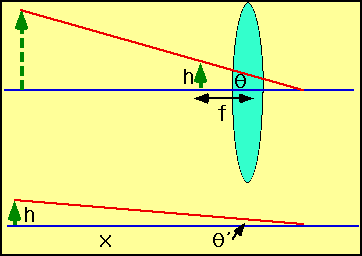
We really use a magnifying glass because we cannot bring
an object nearer to the eye than x ~ 25 cm (the near
point). Hence what we get is angular magnification
M = θ = x
θ' f
What is it in this case?
| 
|
| Since light is a wave, it is possible for it to take different paths to the same point. This leads to interference, if one path is ½λ longer than the other | 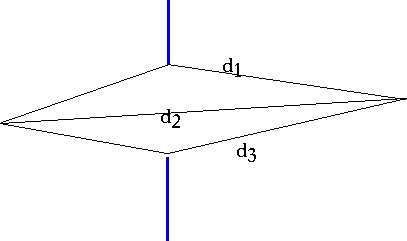
|
| Means that a point will be spread out into a disk, and hence the image of two close objects will overlap | 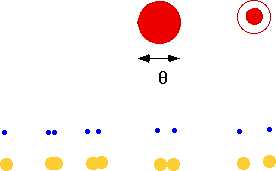
|
θ = 1.22 λ
D
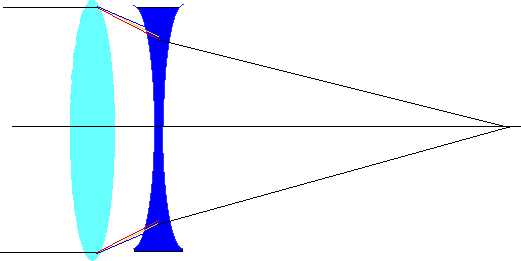
Chromatic aberration:
| Glass disperses light into constituent wavelengths, so get different foci for different wavelengths | 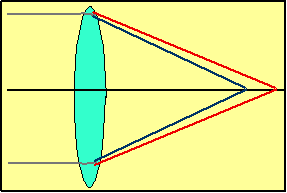
|
| Effect is blurred image | 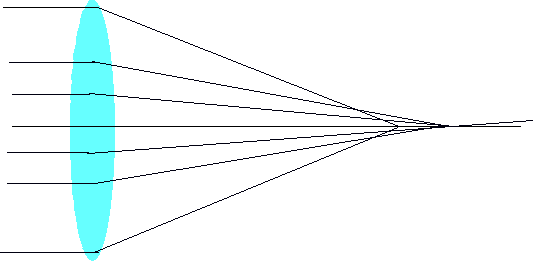 |
| One solution is to eliminate light from outside of lens by stopping down | 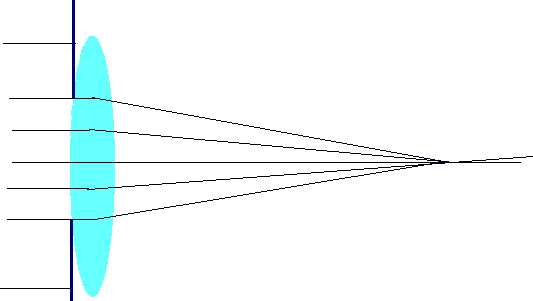 |
| Unfortunately this reduces the area, so you get less light. Only real way out is to go to non-spherical lenses/mirrors. e.g. for a telescope, spherical mirror gives blurred image | 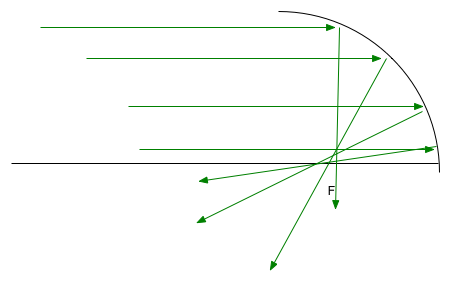 |
| Can be corrected by going to a parabolic mirror (but this only works for objects at infinity) | 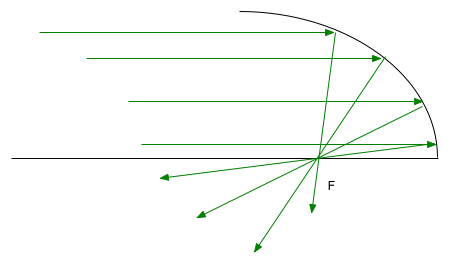 |
| Why does this work? |
|
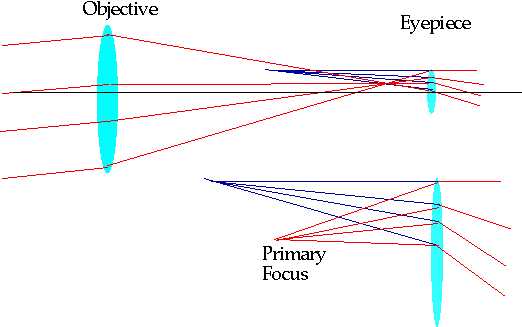
Simplest is two lens refractor. Objective is large
lens at "front", brings light to a primary focus.
Eyepiece is used to magnify image. Magnification: if f₀ is focal length of objective f₁ is focal length of objective
M = f₀
f₁
| 
|
|
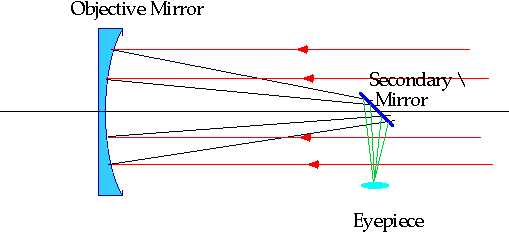
Newtonian reflectors Replace objective lens by mirror: Advantages:
| 
|
| Disadvantage: Spherical Aberration remains | 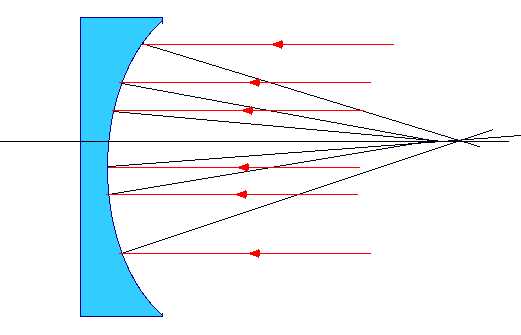
|
| "Best" standard telescope is Schmidt- Cassegrain Corrector plate is very weak aspherical lens to exactly (well, almost) compensate for spherical abberation | 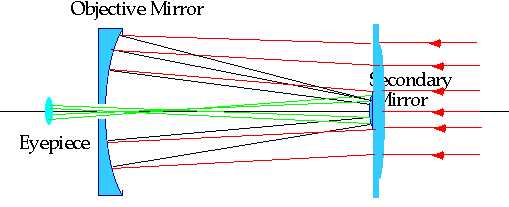
|
| A spectacular picture from the Hubble: large masses can bend light, | 
|
| so a very large cluster of galaxies (about 1013 MSun) can act as a (lousy!) lens. This cluster is producing multiple images of a much more distant galaxy. |  |
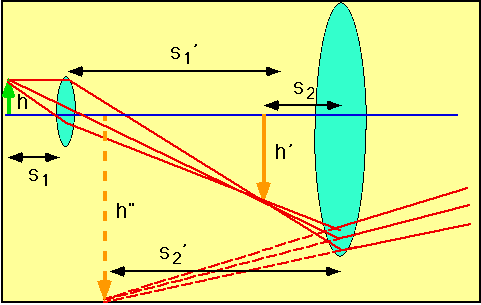
| Objective produces magnified real image of object, which is then magnified by the ocular (eyepiece). Usually have final image at ∞. | 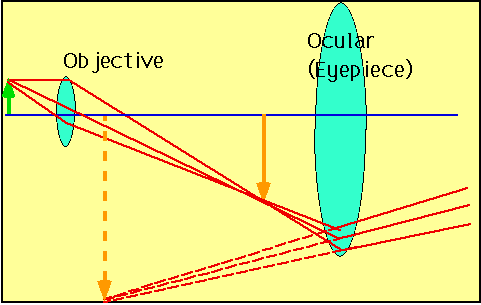
|
Overall angular magnification
M = m₁M₂
=- s₁'x
f₁f₂
|  |
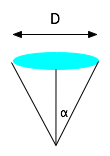
| Note an important practical problem: resolving power for a microscope is
\color{red}{
RP = \frac{{0.6\lambda }}{{n\sin \left( \alpha \right)}}}
This says that we can get below λ by using a wide lens (making α large) and by increasing the refractive index n: e.g. putting the object in oil.:
|
 |