BIT1002 Newton's Laws

By the end of this you should understand Galileo's Law of inertia/Newton's First Law What is an Inertial Frame The Connection between force and Acceleration: F=ma The Third Law of Motion: Action and Reaction are equal and opposite Gravity Examples of other kinds of forces How to solve simple force problems How to handle friction How to solve more complicated problems

First Law (Galileo's law of Inertia):

• A Body continues at rest or in a state of uniform motion unless acted on by a force.

• Uniform motion means no acceleration. Note forces can balance: "a force" means "a net force"

  ---

  Inertial/Non-inertial frames

  • Inertial/Non-inertial frames: A body continues at rest.....

  • At rest with respect to what?

  • Inertial frames: moves at a uniform velocity w.r.t "fixed stars"

  ---

  Non-inertial frames: body accelerates w.r.t. frame without forces being applied

  ---

  A very common non-inertial frame is a rotating one: e.g. a record player turntable.

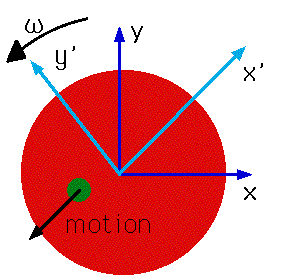  • There are two frames of reference
  • an inertial one (well almost) attached to the earth (x,y)
  • a non-inertial one (x',y')
  • The earth rotates, but is inertial to about 1/2 %.
  • The only truly inertial frame is one defined by the distant stars.

  ---

  Second Law of Motion

  First we need to have concepts of force and mass. Note first that mass is not weight (which is a force!)

  • 2 different objects have same force, different accelerations. Define
    \color{red}{\frac{{m_2 }}{{m_1 }} = \frac{{a_1 }}{{a_2 }}}
    and define arbitrary object to have mass 1 kg.

  ---

  Density

  Closely related to mass is density.
  • Density = mass/unit volume

  •  ρ = M/V
    

  • e.g. 1 litre (=1000 ml = 10^-3 m³) of water weighs 1 kg : ρ = ?

  • The nucleus of oxygen has a mass of 2.7x10^-26 kg and a radius of 3x10^-15m. What is its density?

  ---

  Second Law

  Newton's 2nd law

  • The single most important equation in Physics!

  • Force = mass x acceleration

  • Unit : [F] = [m] [a] = (M) (L T^-2)
  • = kg m s^-2
  • But so important that we need a new unit.
  • 1 Newton = 1 kg m s^-2
    Note this is a vector equation:
    \color{red}{ \vec F = m\vec a}

  How about unbalanced forces?

  If you push a wheelbarrow, it doesn't accelerate, and yet you are supplying a force. This is OK because;

  1. Newton's laws of motion don't apply in the real world
  2. The force is very small compared to the mass of the wheelbarrow, so it cannot cause acceleration
  3. There is an opposing force from the friction between the wheel and the ground
  4. There is an opposing force due to gravity, pulling the wheel-barrow down.

  ---

  Third Law

  Action and reaction are equal and opposite

  • An action is a force exerted by one object on another The reaction is the force exerted by the second on the first

  ---

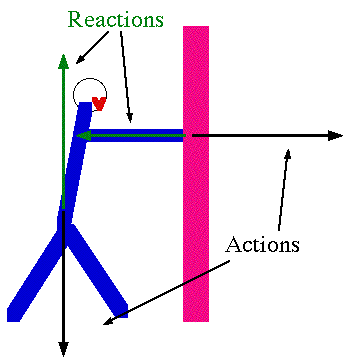  Note that it is particularly easy to forget reaction forces: in this case, if you ignore the reaction force, the block would fall through the table.

  ---

  Examples of Forces:

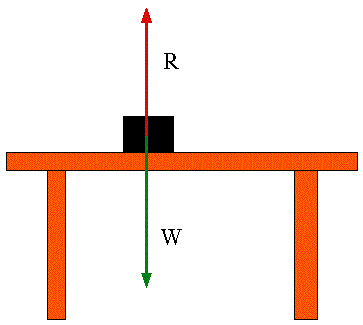  Most important is gravitational force, which gives rise to weight

  • Newton's 2nd. law shows that everything has the same acceleration in a gravitational field

  • m a = W = -mg so that a = -g

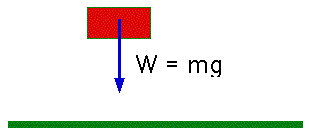  • Gravitational force depends on position:

     F = mg
    

    is a good approx. only at surface of earth. On moon, weight ~ 1/6 that on earth

  ---

  Weightlessness:

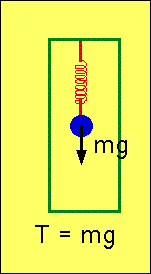
  T = tension in spring. In stationary elevator, or one moving with constant velocity: \color{red}{ T = mg}

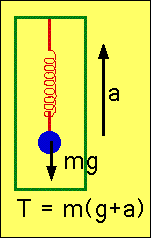
  • In elevator accelerating up with accn. a, Total Force = mass x accn \color{red}{ T - mg = ma \Rightarrow T = m\left( {g + a} \right)}

  ---

  Elevators

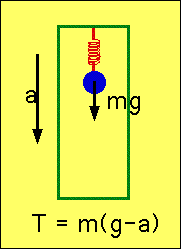
  In elevator accelerating down: i.e. accn = - a, Total Force = mass x accn \color{red}{ T - mg = -ma \Rightarrow T = m\left( {g - a} \right)} both weight and accn. are negative)

  • Weightlessness: Obviously if
    \color{red}{ g = a \Rightarrow T = 0}
    This means the elevator is in free fall

  ---

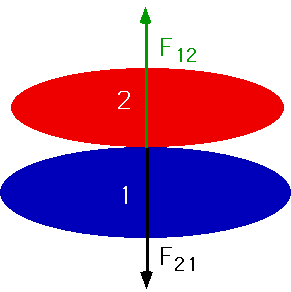
  Contact Forces

  Forces which stop one object penetrating into another. Perp to interface.

  ---

  Elastic Forces

  Response of object to being stretched or compressed

  Tension:

  Ropes provide forces on both ends: you cannot push on a rope. Tension can be measured via (e.g.) a spring balance

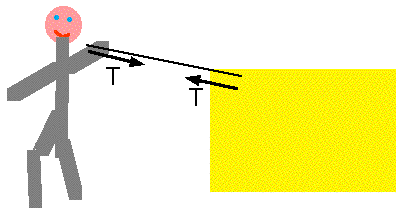  What happens in a tug of war?

  Two teams in a tug of war can each exert a total pull of 2000 N. If a spring balance (calibrated in Newtons) is inserted into the centre of the rope, will it read

  1. 0 N
  2. 2000 N
  3. 4000 N

  ---

  A general strategy for all force problems:

  Remember
  • \color{red}{ \sum\limits_{}^{} {\vec F = m\vec a} }
  • This is a vector equation
  • We must sum over all the forces:
  • Strategy:
  • Draw a diagram with all the forces marked in.
  • Split the problem up so that you are dealing with simple objects.
  • Draw these objects with the forces shown:
  • Resolve the forces into components
  • Solve Newton's 2nd law

  ---

  e.g. A kid pulls two trucks, masses 20 kg and 30 kg, with a horizontal rope.

  If they accelerate from rest to 2 ms^-1 in 4s, what force must he apply?

  First the diagram:

  ---

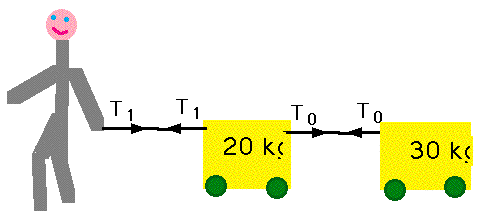  Now split the problem up into individual objects, and draw free-body diagrams. (This is such a simple problem that we hardly need to do this)

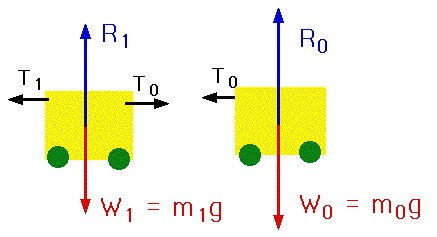  • Now find the sum of the forces for each object, resolved horizontally and vertically

  ---

  Vertically

  • R0-m0g = m0a' = 0

    (for 1st cart: it doesn't fall through ground!)

  • R1-m1g = m1a' = 0

    (for 2nd cart)

    In this case, these eqns tell us nothing!

  ---

  Horizontally
  • \color{red}{T_0 = m_0 a} (first cart)
  • \color{red}{T_1 - T_0 = m_1 a} (second cart)
  • so \color{red}{T_1 = \left( {m_1 + m_0 } \right)a}
  • Finally, we need to solve this using

    \color{red}{v = v_0 + at}

  • This is a very easy problem that we could have solved much less systematically. However the technique is very general.

  ---

  Friction:

  Much harder to deal with.

  • Opposes motion: i.e. if there is a force tending to accelerate a body, friction will always be in opposite direction

  • Force is proportional to the reaction force, and constant changes depending on whether object is in motion or not.

  ---

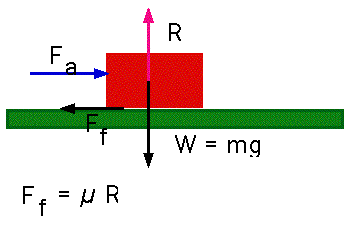  • Friction equals applied force up to some maximum and then is (roughly) constant

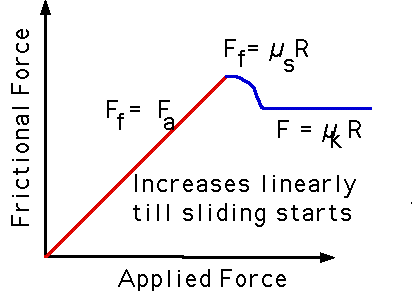  • μ is (roughly) independent of the velocity.
  • Microscopically surfaces are rough and interlock

  ---

  Air resistance

  is a special kind of friction. Force~ (velocity) or Force~(velocity)²

  • In this case the force (and hence the acceleration) is not constant: has to be solved by numerical method

  ---

  Fair = 1/2 C A ρv2 where C is a number that depends on the shape (Note it's dimensionally correct) ρ is the density of the fluid (in a vacuum, the air resistance is zero!) Fgrav = -mg

  ---

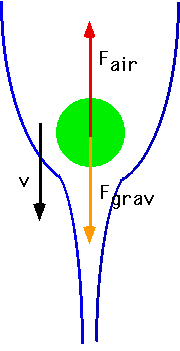  However, can find terminal velocity quite easily.
  • This will occur when there is no net force (remember the first law: things don't have to be at rest)

    hence terminal velocity is given by vterm = (2 g m/CAρ)1/2 C~ 0.5, ρ~ 1.3 for air

  • For a man of 70 kg, A = .5m², v = ?

  ---

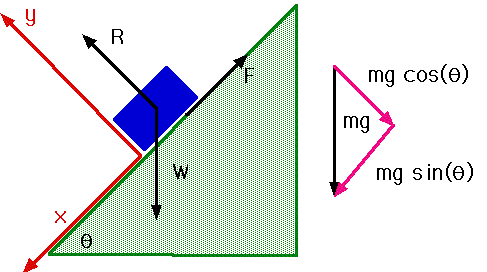
  Sloping surfaces

  (i.e.inclined planes)

  • Usually best to resolve parallel and perpendicular to plane
  • e.g. a block is on an inclined plane with slope of 450 and a (kinetic) coef. of friction of 0.2. What is its acceleration?

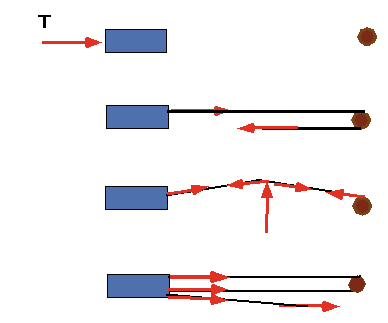
    You have just driven your car into a snow-bank on a country road. There is a tree across the road, and you have a length of rope in the car. As a student who has just passed BIT1002, you know that this is a physics problem.

    Do you Get behind the car and push? Tie the rope round the bumper of the car and use the tree as a pulley to move it? Tie the rope round the bumper of the car and the tree, and push on the middle of the rope? Tie the rope round the bumper, loop it round the tree and back round the bumper, so it can slide on both of them, and pull on the rope? Wait for a tow- truck to happen by?

    Now we go to Energy