BIT1002 Work and Energy

Work and Energy

Newton's second law gives us a relation between velocity and force, via

F = m a = m δv 
            δt

If the force is complicated (e.g. F = -kv², or F = sin(r) ), then solving for the velocity can be very difficult. Fortunately there is a better way.

Work

First need to define Work

Work = Force x Distance (at least to start with)

W = F s

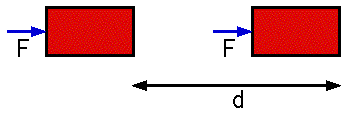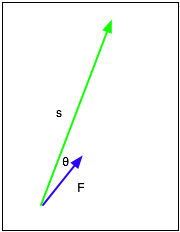
If the force is at an angle to the displacement, then it will be less effective in causing accn. Hence define

         W = F s cos(θ)

Note you do no work to a bucket of water if

you sit and watch it (s = 0)

you carry it all day! (θ = π/2, cos(π/2) = 0)

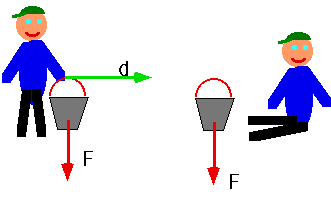Note that we have multiplied two vectors together here

Define scalar product of two vectors

 W = F.s

to mean

W = \color{red}{{\vec F}}x(component of \color{red}{{\vec s}} in direction of \color{red}{{\vec F}})

W = Fs cos(θ)

(note scalar product is a scalar!)

Note that if the displacement is opposite in direction to the force, the work is negative Done properly:: both Force \color{red}{{\vec F}} and displacement \color{red}{{\vec d}} are vectors: for any vectors \color{red}{\vec F.\vec s = \left| {\vec F} \right|.\left| {\vec s} \right|\cos \left( \theta \right) = Fs\cos \left( \theta \right)} so (e.g.) \color{red}{ \vec F.\vec F = F^2 } so

\color{red}{ \hat i\,.\hat i = \hat j.\hat j = \hat k.\hat k = 1}

(since they are unit vectors!) and

\color{red}{ \hat i\,.\hat j = \hat i.\hat k = \hat k.\hat j = 0}

since they are perpendicular. Hence if

\color{red}{ \begin{array}{l} \vec s = x\hat i + y\hat j + z\hat k \\ \vec F = F_x \hat i + F_y \hat j + F_z \hat k \\ \end{array}}

\color{red}{ \begin{array}{l} \vec F.\vec s = F_x \hat i.x\hat i + F_x \hat i.y\hat j + ..... \\ = F_x x + F_y y + F_z z \\ \end{array}}

e.g. suppose

\color{red}{ \begin{array}{l} \vec s = 3\hat i + 4\hat j \\ \vec F = 5\hat i + 12\hat j \\ \end{array}}

What is s?

5
-5
7
25

e.g. suppose

\color{red}{ \begin{array}{l} \vec s = 3\hat i + 4\hat j \\ \vec F = 5\hat i + 12\hat j \\ \end{array}}

What is F?

5
13
17
12/5

e.g. suppose

\color{red}{ \begin{array}{l} \vec s = 3\hat i + 4\hat j \\ \vec F = 5\hat i + 12\hat j \\ \end{array}}

What is \color{red}{\vec F.\vec s}

63
24
63^1/2
56

e.g. suppose

\color{red}{ \begin{array}{l} \vec s = 3\hat i + 4\hat j \\ \vec F = 5\hat i + 12\hat j \\ \end{array}}

s =5
F = 13
s.f = 63

. What is the angle between them?

0⁰
90⁰
cos^-1(63/65)=14.3⁰
sin^-1(63/65)=75.7⁰

e.g. Lifting an object, mass m through height h

Work done by gravity
= -m g h

Work done by you
= F h

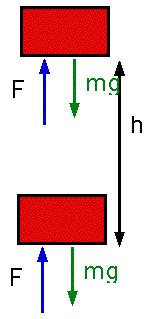Assuming the block is moving at uniform velocity,

F = mg

Work is only useful because it lets us introduce a new idea called Energy.

Kinetic Energy

defined to be

  T = ¹/₂ m v²

for a particle with mass m, vel v.

If we have a constant accn.
v² = v₀² + 2 a s

mult. both sides by ¹/₂m gives

      ¹/₂mv² = ¹/₂mv₀² + m a s

but

ma = F

so this can be rewritten

 Fs = ¹/₂mv² - ¹/₂mv₀²

Work done = change in kinetic energy. Watch the animation!

This result is completely general: We have proved it for constant acceleration in 1-D, but it works for any force in 3-D.

Conservative Forces:

Fortunately for a lot of forces, the W.D. depends only on the endpoints.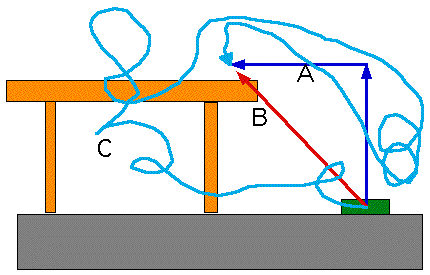

e.g. along route A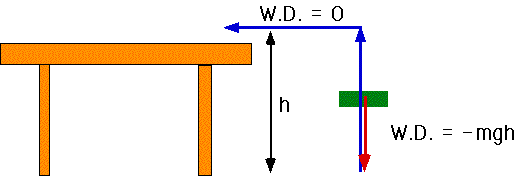

e.g. along route B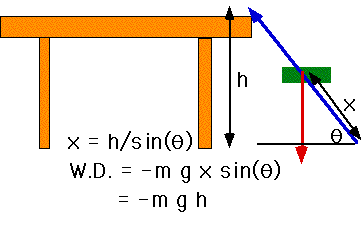

Complicated paths can be simplified.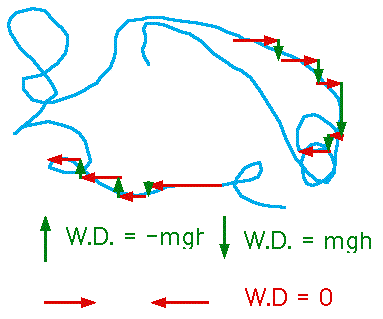

Whatever the path, the W.D. by gravity is the same

W.D. by gravity
= -mg(h-h₀)

where h₀,h are the starting and ending position respectively

Potential Energy

Which leads us to Potential Energy: If W.D. is independent of the path, then Force is conservative and we can define Change in P.E. = -(work done along path)

e.g. Gain in P.E. by raising an object a height = mgh

So What?

Since

W.D. = Change in K.E.

and

W.D. = - Change in P.E.

Then

Change in K.E. + Change in P.E. = 0 i.e.

 Total energy = P.E.+ K.E.= constant

Watch the animation!

Note that the force would be very complicated in this case, so one couldn't actually solve via F = ma

Units

Need a new unit for energy

[¹/₂mv²] = M L²T^-2 = kg m²s^-2

1 Joule= 1 kg m²s^-2

(Joule originated study of heat energy ⇒ mechanical energy)

Another very useful unit of energy is the Electron Volt (eV)

1 eV = 1.602x10^-19 J

(Origin later)

Conservation of Energy

A very important idea that we will return to again and again:

If the forces are conservative, then total (mechanical) energy will be conserved: it can be transformed from one form to another. (P.E. ⇔K.E.)

Later will see that energy is always conserved, but we need to introduce more kinds:

Heat⇔chemical ⇔ potential ⇔ nuclear ⇔kinetic

e.g. What should the world pole vault record be? (5.8 m at present).

Assume that the vaulter runs at 10 ms^-1, and his c.o.m. is 1 m. above the ground

Note (Very Important)

Only Differences in P.E. are meaningful

 δU = mg(h-h₀)

It doesn't matter where we choose h to be measured from

How do I decide if I have a conservative force?

If you can get the energy you put into the system back, it's conservative. e.g. all fundamental forces (gravitational, electromagnetic, nuclear..) or..........

If the work done is independent of the path, then if one goes round a closed path which returns to the starting point, the W.D. is zero

Hence friction cannot be a conservative force

W.D. = - 4 d F

In general, Work-energy theorem has to be changed if we have non-conservative forces

Total work = change in K.E. (always)

work done by conservative forces + work done by non-conservative forces = - change in P.E. + WD_nc

WD_nc= δT + δU

e.g A 70 kg skier goes down a slope with a vertical drop of 100m and a length l=.5 km. If his terminal velocity is zero, what is the average friction? What would the speed be if l = 250m?

Perpetual Motion Machines

We would be able to arrange for a complicated system of forces to keep things moving forever.

which turns for ever

Or another variety
which also turns for ever

and here is a modern version of the

overbalancing wheel

Conservation of energy tells you not even to try! (and the US patent office requires a working model of a perpetual motion machine...!). However, that doesn't stop people from trying.. These come from two fascinating sites. See here (by R Woods) and here (by Eric Dennis).

Gravitational P.E.

We have to use calculus!

We have

\color{red}{ F = - \frac{{GMm}}{{r^2 }}}

(the minus sign gets the direction correct)

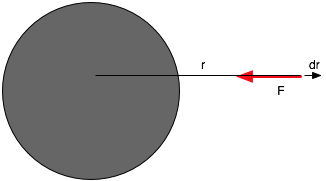Suppose we move it the point a little further (δr) from the earth:
\color{red}{ W.D. = dW = \vec F.\delta \vec r = - \frac{{GMm}}{{r^2 }}\delta r}

Now we need to find the total work done:

\color{red}{ W.D. = \sum\limits_{}^{} { - \frac{{GMm}}{{r^2 }}\delta r \Rightarrow } - \int {\frac{{GMm}}{{r^2 }}dr} }
Change in P.E. = - W.D.
For gravity in general, (not close to earth's), can use the freedom to measure from any particular point to set U(∞) = 0
Then we get
\color{red}{ U\left( r \right) = \int_r^\infty {\frac{{GMm}}{{r^2 }}dr} = - \frac{{GMm}}{r}}

This doesn't look much like the usual form

U(h) = mgh

but................

In fact the slopes are the same near the surface of the earth

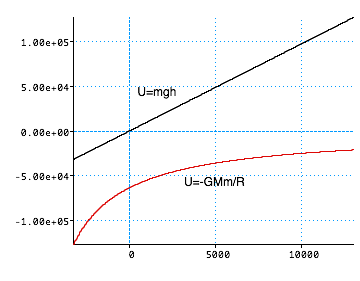
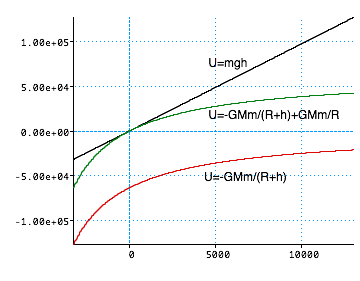
Satellite in orbit at distance r from earth.

\color{red}{ K.E. = \frac{1}{2}mv^2 ,P.E. = - \frac{{GMm}}{r}}

and

\color{red}{ \frac{{GMm}}{{r^2 }} = \frac{{mv^2 }}{r}}

So Total Energy

\color{red}{ T.E. = - \frac{{GMm}}{{2r}}}

This is quite general: a system of two or more particles bound together will have negative energy. Also

K.E. = - ¹/₂ P.E.

Escape Velocity How hard would you need to throw something so that it never came back?

At the earth's surface,
At ∞, P.E. = 0, so want K.E. = 0 as well
Remember T.E. = P.E. + K.E. = constant
\color{red}{ \frac{1}{2}mv^2 = \frac{{GMm}}{r} \Rightarrow v = \sqrt {\frac{{2GMm}}{r}} }
e.g. for the earth: R = 6500 km g = 9.8 ms^-2
v_escape
=???

How big would the earth need to be so that escape velocity = c?

What does this mean?
Warning: this argument is totally dishonest! We lucked into the correct answer!

General strategy

General strategy for all Energy problems

Define the system and draw a diagram
Work-energy can be used if you are asked for (e.g.) the final velocity. It cannot be used (usually) if you are asked for times.
Decide if all the forces are conservative (More difficult if they are not)
Choose a zero-point for P.E.: usually where you start from (e.g uncompressed spring) but can be r = ∞ for grav. problem.

If no friction, then use

(PE + KE)_start = (PE + KE)_end

If friction

W.D_friction= δPE + δKE

e.g.

a pendulum has a bob with a mass of 500 gm and a length of 40 cm. If it is held horizontally and released, how fast is it travelling when gets to the bottom of its swing?
What will the tension in the string be at the bottom?

e.g. ( a bit harder) a dam holds up water. Assume the reservoir is 2 km long, 200 m wide and 50 m high, how much energy is stored?

Power

Rate of doing work Unit: 1 watt = 1 Joule/sec = 1 kg m² s^-3

e.g. a man climbs a 3 flights of stairs (4 m each) in 6 s. If his mass is 70 kg what is his power output?

Unit is rather small: often use 1 Horse-power = 746 watts

lightbulb consumes 10-150 W
Home-heating ~ 1-5 kW
Output of power-station ~1GW = 10⁹W
Car engine ~ 10 kW
Note (very confusingly) 1 kilo-Watt hour (kWh) is unit of energy
1 kWh = 60x60x1000 J = 3.6 MJ Unit that electrical energy is sold in

I was stupid enough to live in a farm-house with a drilled well 460 ft. deep

If I have a ³/₄ h.p. motor, can I get a bath?

In limit, Instantaneous power

P = δW 
    δt

An alternative way of writing this:

δW = F.δs

δW = F.δs = F.v 
δt     δt

so...

Power = Force x Velocity

e.g. a car has a max. power output of 30 kW, and the air resistance is given by

F = ¹/₂ cρAv².

What is its maximum speed, if c = 0.5, A = 2m² and ρ = 1.3?
How much power is used at 80 km/hr?

Now we need to go back and look at rotational motion a bit more seriously

We would be able to arrange for a complicated system of forces to keep things moving forever.
which turns for ever