Kinematics in Two Dimensions

Swish! by alanfreed

Kinematics in 2-dimensions. By the end of this you will

Remember your Trigonometry
Know how to handle vectors
be able to handle problems in 2-dimensions
understand projectile motion

Two (or Three) Dimensional Motion

For example: Projectiles, Planets, Pendulum, ....

Need to have some new mathematical techniques to do this: however you may need to revise your basic trigonometry

Basic Trigonometry

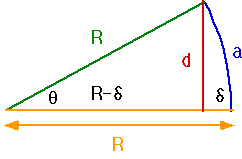
Basic Definitions of trig relationships

A useful mnemomic

SohCahToa

θ =  a  
     R 
Sin = opposite  =  d  
      hypotenuse   R 
Cos = adjacent  = R-δ 
      hypotenuse   R 
Tan = opposite  =  d        
      adjacent    R-δ

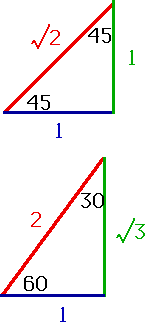
Basic Trig.

Useful relationships

sin²θ + cos²θ = 1 (all values of θ)
tan θ = sin θ / cos θ

These are not so useful

cot θ = 1/tan θ
sec θ = 1/cos θ
cosec θ = 1/sin θ

Special Values

sin(45⁰) = sin(π/4) = 1/√2

cos(45⁰) = cos(π/4) = 1/√2

tan(45⁰) = tan(π/4) = 1

sin(30⁰) = sin(π/6) = 1/2

cos(60⁰) = cos(π/3) = 1/2

sin(60⁰) = cos(30⁰) = √3/2

tan(30⁰) = tan(π/3) = 1/√3

tan(60⁰) = tan(π/6) = √3

sin(90⁰) = sin(π/2) = 1

cos(90⁰) = cos(π/2) = 0

tan(90⁰) = tan(π/2) = ∞

These are worth writing down, but they are very easy to work out.

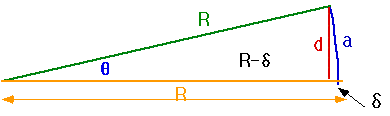
We often have a convenient simplification when the angles are small

θ = a/R ~ sin(θ) = d/R ~ tan(θ) =  d (R-δ)

cos(θ) ~ 1

Note that this only works if we measure angles in radians:

2π radians = 360⁰

Vectors

Need new mathematics to describe three dimensional objects:

Scalars: quantities with only magnitude

Vectors have direction as well

Scalars Vectors
Temperature Force
Speed Velocity
Density Acceleration
Time? Time?

Need a new symbol: can use

${\vec a}$ which is obvious
a which gets confused with other symbols
a, which is hard to read

We will use both ${\vec a}$ and a,

Need to be able to describe vectors in terms of scalar quantities: can do this in terms of components: the projection of the vector along each axis

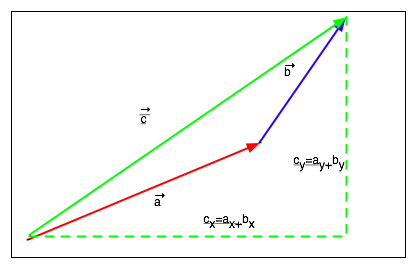
These are the components of the vector ${\vec a}$
Note that the components of a vector are scalars

Also can do this in terms of length of the vector and angle(s).

These two descriptions are related

a_x = a cos(θ) a_y= a sin(θ)

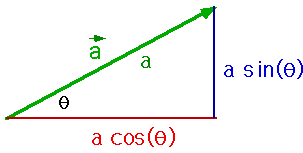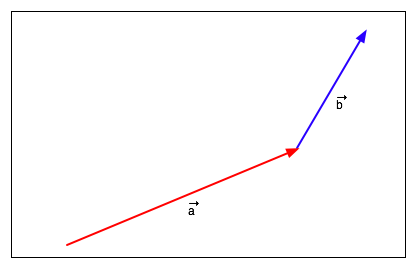
Adding vectors: put them nose to tail. Easy diagramatically

If we want to add them algebraically, we just add the components:

$$ \color{red}{ \vec c = \vec a + \vec b} $$
means $$ \color{red}{ \begin{array}{l} c_x = a_x + b_x \\ c_y = a_y + b_y \\ \end{array}} $$

To subtract vectors, Flip the vector round: the negative of a vector must add to the vector to give zero

${\vec a}$ - ${\vec a}$ = ${\vec a}$ + ( -${\vec a}$) = 0

Note that this means that the negative of a vector just has all its components reversed

The length of a vector is given by Pythagoras: 3-D analog of Pythagoras:

Write this as

\color{red}{ \left| {\vec r} \right| = \sqrt {x^2 + y^2 + z^2 } }

Note:

The length of a vector is a scalar.
Displacement is a vector.
The length of the displacement vector is the distance

Examples

e.g. a boat sails 10 km North -East and 5 km South: how must it sail to get to its start?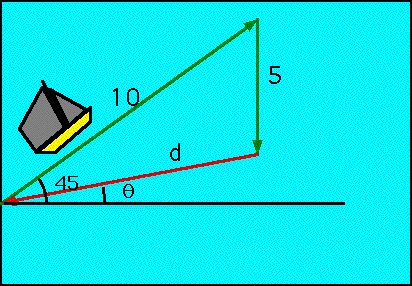

How do we write this as a vector sum?
N.E means "equal components along the x and y directions" so first step is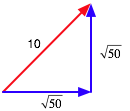

e.g. Motion by a car.

A car travels 5 km N, 10 km E, and then 15 km S. The components of vector ${\vec a}$ that describes this are

```
a_x = -10 
a_y = 20 
```
```
a_x = 10 
a_y = -10
```
```
a_x = 10 
a_y = 10
```
```
a_x = -10 
a_y = -10
```

We write this as

Projectile Motion

(can usually be treated as 2-D)

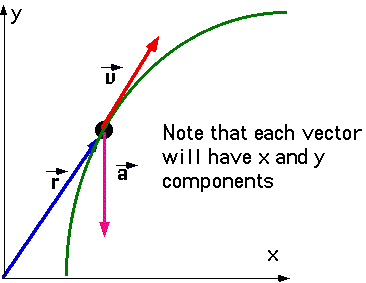
Treat position, r, velocity v and acceleration as 2-D vectors. In general,motion in one direction can be treated independently of motion in a second.

We can also see this quantitatively

In general there are three independent vector quantities:

The position r, the velocity v and the acceleration a. However we have to treat the components separately.

It is easiest to treat the two motions as independent 1-D motions

\color{red}{\begin{array}{l} v_x = v_{0x} + a_x t \\ x = v_{0x} t + \frac{1}{2}a_x t^2 \\ a_x = 0{\rm{ (usually)}} \\ \end{array}}

\color{red}{\begin{array}{l} v_y = v_{0y} + a_y t \\ y = v_{0y} t + \frac{1}{2}a_y t^2 \\ a_y = - g{\rm{ (usually)}} \\ {\rm{ = - 9}}{\rm{.8 ms}}^{{\rm{ - 2}}} \\ \end{array}}

Can combine these to give (e.g) an equation for the range R:

What is value of t when the height y = 0?
\color{red}{ t = \frac{{2v_0 \sin \left( \theta \right)}}{g}}
(or t = 0: what does this mean?)
Hence Range
\color{red}{ R = \frac{{v_0 ^2 \sin \left( {2\theta } \right)}}{g}}

e.g. a ball is thrown at 15 ms^-1, at 30⁰ to the horizontal.

How far does it go
How long is it in the air?

Relative Velocity

Example: a woman who can swim at 2 m/s is swimming

How fast does she swim upstream?
How fast does she swim downstream?

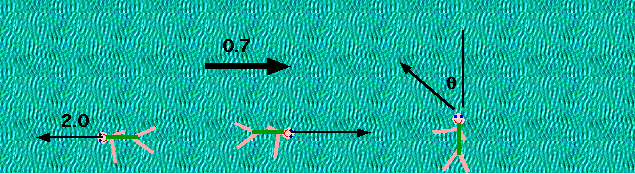
in a river which flows at .7 m/s.

How about a round trip?

A woman swims 100 m upstream at 2 m/s in a river with a current of .7 m/s, and then 100 m downstream to return to her starting point. Compared to swimming 200 m in still water, does her journey

Take longer?
Take a shorter time?
Take exactly the same time?

As a somewhat more sophisticated example: a woman who can swim at 2 m/s is swimming in a river which flows at .7 m/s.

At what angle should she swim to reach a point on the opposite bank immediately opposite the point from which she starts?

Now we want to describe why things move, not just how.

Scalars	Vectors
Temperature	Force
Speed	Velocity
Density	Acceleration
Time?	Time?