PHYS1008: Quantum Mechanics and Reality

Objectives: by the end of this you should be confused! have a feeling for how complex the real workd is. understand what it means when we measure something understand what we mean when we talk about uncertainty and probability in quantum mechanics.

• We have used quantum mechanics as a tool: does it just disguise something deeper?

• I think I can safely say that nobody understands quantum mechanics. Richard Feynmann.

• So what is this wave thing?

Waves and Particles

• Since the electron behaves as a wave, can do a Young's slits type experiment, and get usual 2 slit interference pattern:

• This shows how it actually builds up in practice

  (Hitachi: http://www.hqrd.hitachi.co.jp/em/movie.cfm

• But the electron is a particle, with charge. It must go through one slit or the other...

  Suppose we close off one slit: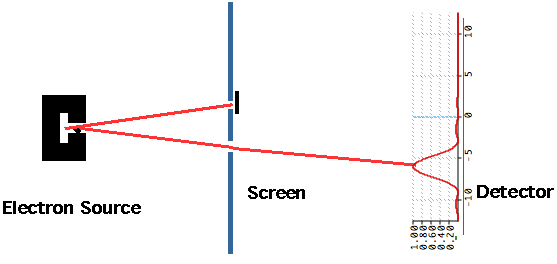

  ---

  Suppose we close the other slit:
  Note when we add together two one slit patterns, we do not get two-slit patterns.

• Now we get sum of one slit patterns, but not a 2 slit pattern!
• What happens if we use a detector that only picks up one electron in two?
• More worrying than this: we can do a "delayed choice" experiment: don't try to observe the electron until after it has gone through one of the slits...that still destroys the pattern.
• Conclusion We cannot decide which slit the electron went through without destroying the pattern. Observing something fundamentally changes it!

• There was a young man who said "God
  Must think it exceedingly odd
  That this tree
  Continues to be
  When there's no one about in the Quad"

• Uncertainty principle largely misunderstood by philosophers: the practical limits on measurement are much larger. However the idea that observing a system automatically changes it has had significant impact e.g.
  • Anthropologists know they cannot observe an primitive society without altering it.
  • Hawthorne effect in psychology

What Waves?

• so that if it hits a potential hill

  slow electron is always reflected (low energy) fast electron always goes over (high energy)

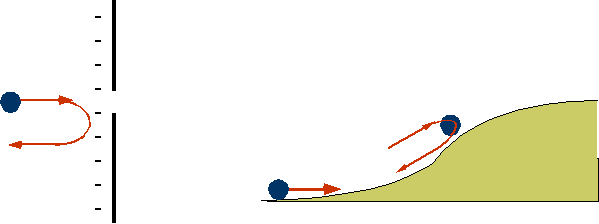• Waves do not behave like this: they get partially reflected (remember what happens to light hitting glass).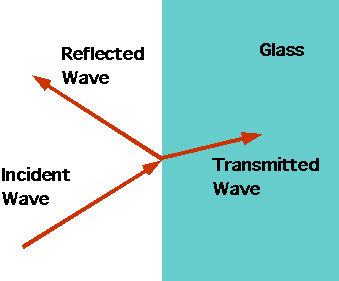

• If electron is literally the wave,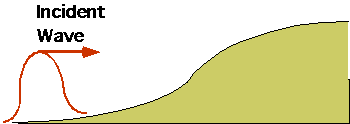

• this would imply we see 1/2 electrons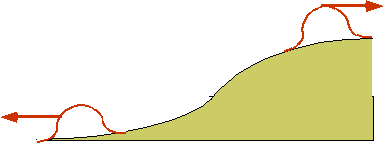

Probability Interpretation

• P = |Ψ(x)|²

• e.g. for the electron in a box, in the first excited state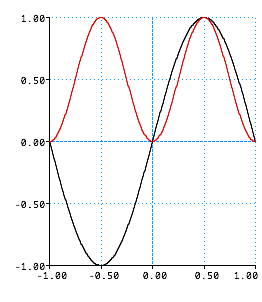

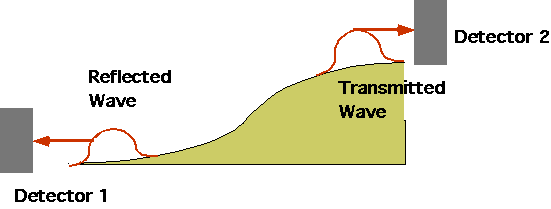
• Note electron must be somewhere: i.e. probability of detecting it somewhere = 1
• Think of a die:
• probability of any given face = 1/6
• probability of any face being uppermost = 1

• Back to barrier problem

  Probs must add to 1: P₁ = prob. that electron hits detector 1: P₂ = prob. that electron hits detector 2 P₁ + P₂ = 1

• • 481 could hit 1
  • 519 ------------ 2
  (Maybe)
• 1000 will hit 1 or 2
• But we cannot say what any individual electron will do
• Classical Determinism
• Given state of solar system in (say) 100 A. D., can use Newtonian mechanics to predict earth's position now
• Quantum mechanics:
• Can only predict most likely (probable) position now.
• Morals
  1. Macroscopic (i.e. large) objects are predictable, electrons aren't!
  2. Cannot ask "what happens?": can only ask "what can we measure?"
  3. No reason to assume that rules deduced for macroscopic objects are true for very large/very light/very fast objects. "What colour is an electron?"

• E.g.: suppose we measure the position of a particle and it was at C

                       x                 
                       C
  

• Where was it just before?
• Classical Mechanic At C.
• Quantum Mechanic Somewhere: it was only measuring it that fixed its position . Where is a candle flame after it is blown out?

Measurement

• In classical mechanics, we believe that a object is the same whether we measure it or not.
• In quantum mechanics, until we have measured it, its condition is indeterminate.

• e.g a H atom in the first excited state (n = 2)will decay to the ground (n = 1) state in about 10-10 s. and emits a photon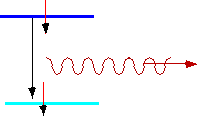

• Can measure this in various ways: e.g
• By seeing the photon
• By measuring the radius of the atom (n = 1 is half the size).

• if we create it in the excited (n = 2) state, and wait, it will start being a mixture of the 2 states.

  Initially it is almost all the upper state

• After some time it's a 50-50 mixture

• Finally it is almost all the lower state

By measuring the atom, we can decide which of the two states it is in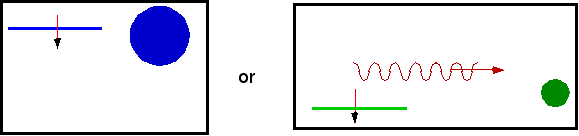

e.g. consider light going through 2 sheets of polaroid at 90°.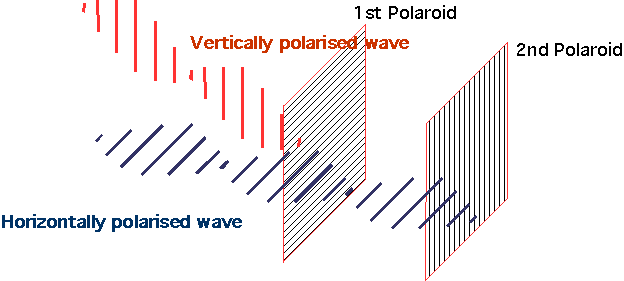

Classical Mechanic: First sheet eliminates all vertically polarized light Second sheet eliminates all horizontally polarized light Result: darkness Quantum Mechanic: First sheet measures how much of light is polarized in horizontal direction, and produces a new wave polarized horizontally Second sheet measures how much of light is polarized in vertical direction, but there isn't any.. Result: darkness .

Now insert a third sheet at 45° between the two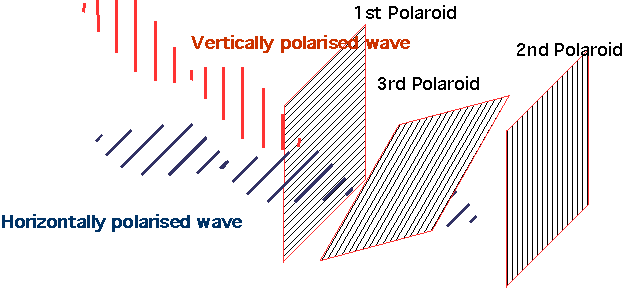

• Classical Mechanic:
  1. First sheet eliminates all vertically polarized light
  2. Third sheet eliminates all light polarized at 45⁰
  3. Second sheet eliminates all horizontally polarized light
  4. Result: darkness
• Quantum Mechanic:
  1. First sheet measures how much of light is polarized in horizontal direction, and produces a new wave polarized horizontally
  2. Third sheet measures how much of light is polarized at 45⁰ direction, and produces a new wave polarized at 45⁰
  3. Second sheet measures how much of light is polarized in vertical direction, produces a new wave polarized vertical
  4. Result: light
• 
• D uuuuuuh!!!!

EPR

• E.g. go back to our wave function example:

• This seemed to say that the electron gets split in half, but we interpreted it as a probability.

• But when did the electron decide which way it was going?

• The Einstein-Podolsky-Rosen paradox (EPR) is a more sophisticated version of this.

• We can have a particle with no spin which decays into 2 particles with spin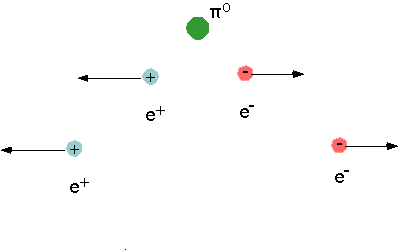

• There are two possibilities for the way the spins can arrange themselves: up-down

• There are two possibilities for the way the spins can arrange themselves: down-up

  .
• When does the electron and positron make up their minds as to which way they are going to spin?

• Classical Mechanic Obviously when they are created, their spins will be fixed.

• Quantum Mechanic It is indeterminate until you measure them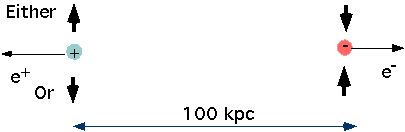

• EPR Don't be stupid. Measuring the spin of one would automatically defines the spin of the other. They could be separated by any distance, how does the second one know how to fix its spin?

• God does not play dice. Einstein

• Hence the only logical way out is "hidden variables": underneath quantum mechanics, there is a much more complicated theory where everything is deterministic.
• it only looks random on the surface.

Schrödinger's Cat

The sophisticated version: you have a box, with a lid and a single radioactive atom: when the atom decays, cyanide gas is released.

• Take a cat
• Put it in the box and close the lid.
• Is the cat dead or alive?
• Classical Mechanic Obviously its either dead or alive
• Quantum Mechanic It is indeterminate until you measure it . More exactly, the cat is a mixture of alive and dead cats: the measurement fixes it.
• Schrödinger Don't be stupid.

• Bell's theorem shows that there are measurements that you can do on the polarizations of the particles which are incompatible with any conceivable hidden variable theory.
• Aspect did the experiment.
• The Schrödinger's Cat experiment has been done:
• No animals were injured in the making of this movie.
• One atom: process is totally random, so you can't decide if a one-atom cat is alive or dead without measuring it(!)
• Many atoms (10²⁹): constitutes an independent measuring system, so the cat measures it's own deadness
• Few atoms (2-20): process becomes steadily more predictable

• God not only plays dice, but throws them where they cannot be seen. Hawking

EPR thought the states must be separate

They are actually one "entangled" state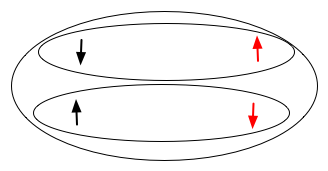

and a measurement destroys it: e.g.

• Alexandre Blais
• Departement de Physique
• Universite de Sherbrooke
• Friday 2007 March 23 11:30
• room Azrieli Theatre 101.
• Quantum computers would take advantage of the "most bizarre aspects of quantum mechanics" (superposition of states and entanglement) in order to, in principle, perform calculations exponentially faster than any classical computer could. The experimental realization of such a quantum computer is however an enormous challenge. Assuming no knowledge of quantum mechanics, I will present some of the fundamental ideas of quantum information. I will also discuss how these ideas could be realized experimentally.

The quantum Zeno effect

or the "watched pot effect":

• If measuring something really matters, then we can "reset the clock" by making sure that nothing has happened.
• Hence watching a cold pot on a stove makes sure it never boils:
• in more sophisticated language, if you continuously measure the state of an atom to make see if it hasn't decayed, then it can't!

Conclusions:

• Either

  Quantum mechanics is correct, and there is no "simpler" system

• Or

  Reality is even uglier than we thought: e.g.

• non-local hidden variables: every bit of the universe is involved with every other bit

• Many-worlds theory: every time a measurement is made, the universe subdivides into separate universes that correspond to every possible outcome of the theory

• ????????????
• (Ugh!) Does it bother you that 20th century technology depends fundamentally on something no-one understands?
• So lets look at another aspect of quantum mechanics: nuclear physics