
Orion: the red colour is (mostly) hydrogen.
- Why we need photons
- how Bohr managed to understand the hydrogen atom
- How atoms radiate
- What energy levels are
- Why the Bohr model didn't really work
 Orion: the red colour is (mostly) hydrogen. |
Objectives: by the end of this you will understand
|
| Wien noticed that experimental curve looked like Maxwell-Boltzmann distribution. for molecules |  |
E = 1/2 m v²
f λ = c
E = h f
h = 6.6 x 10-34 Js = 4.1 x 10-15 eV s
E = hf = hc/λ
Since particles have energy, photons must carry energy (obviously light has energy: that's how you get a sun tan!)
|
Einstein (1903): (note this was what he actually got the
Nobel prize for) adapted Planck's hypothesis to say that light is
absorbed in quanta (photons). Most energetic electrons in metal need extra boost to escape: |
 |
K.E. = 1/2mv²= hf-φwhere φ is work function: differs for different metals. Slope is universal ⇒ Planck's constant |
 > > |
fλ = c
(frequency x wavelength = speed)
E = h f
| Electrons are ejected as soon as light strikes (no need for energy to accumulate), since photons arrive randomly | 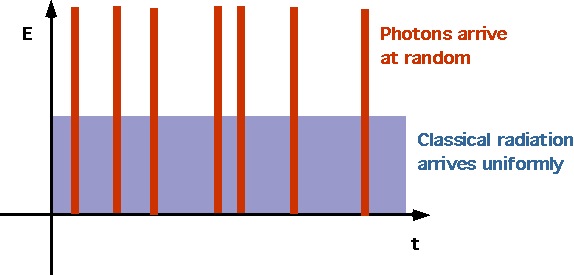 |
| "Classical" corks bob up and down | 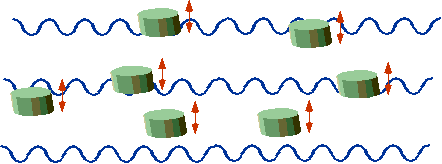 |
| "Quantum" corks are either stationary or ejected. | 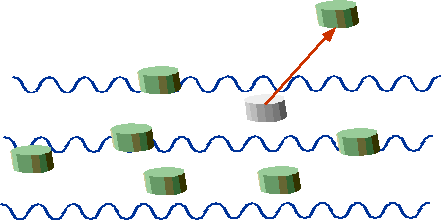 |
|
λ |
f | E | |
| γ-rays |
10-13 |
3 x 1021 |
12 MeV |
| UV |
10-7 |
3 x 1015 |
12 eV |
| Visible |
6 x 10-7 m |
5 x 1014 |
2 eV |
| Radio | 300m | 106 | 4 x 10-9 eV |
| Gives the "energy" part of the spectrum. | 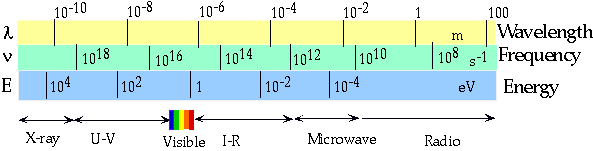 |
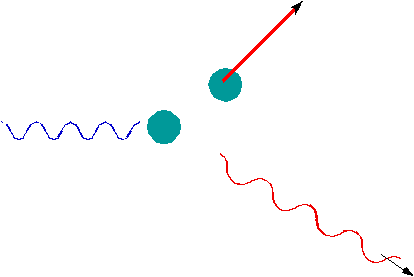
A photon can scatter off an electron like a billiard ball, in which
case, instead of
Ee = h fwe would get Ee = h f - h f' |
 |
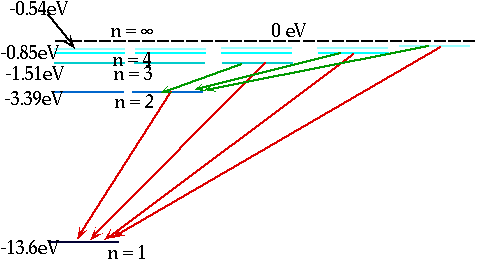
Model for H. atom must explain
n = 1 m = 2, 3, 4... n = 2 m = 3, 4, 5... n = 3 m = 4, 5, 6...
electrostatic force = centripetal force
FE = QeQp = mv²
4πε₀r² r
|
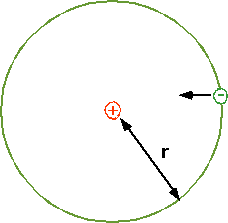 |
Qe= - Qp = e
because!
\color{red}{
\begin{array}{l}
E_n = - \frac{1}{2}\frac{{e^2 }}{{4\pi \varepsilon _0 R_n }} = - \frac{1}{2}\frac{{e^2 }}{{4\pi \varepsilon _0 }}\frac{{me^2 }}{{4\pi \varepsilon _0 n^2 \hbar ^2 }} \\
= - \frac{1}{2}\left( {\frac{{e^2 }}{{4\pi \varepsilon _0 }}} \right)^2 \frac{m}{{n^2 \hbar ^2 }} = - \frac{{13.6}}{{n^2 }}eV \\
\end{array}}
|
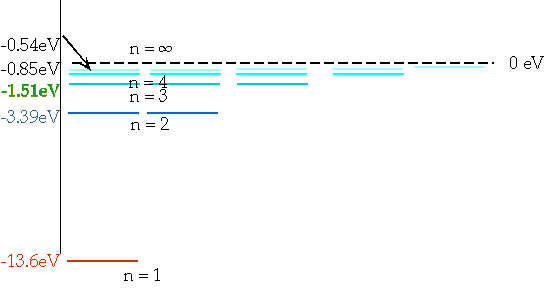 |
En = = - 13.6 eV
n²
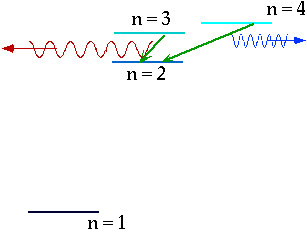
e.g. n = 3 ⇒ n = 2δE = E3 - E₂ = 1.9 eV |
 |
|
 |
Are these energy levels so weird?