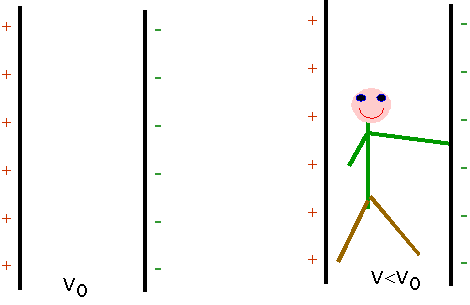PHYS1008 Electric Potential
 Electrostatic potential surface of chlorobenzene Oliver Kamp, Carsten Biele, Gregor Fels
|
Objectives: By the end of this you should understand
- the reasons for using potential
- the difference between potential and field
- the potential for a point charge, dipoles and flat plates
- The Oscilloscope
- how to use electric potential in simple cases
- the analogy of electric charge as a fluid
- Equipotentials
- How Conductors and Insulators modify fields and potentials
- Electrical Breakdown and the Van der Graaf generator
- the basic idea of capacitance
- how to calculate it in simple cases.
- how capacitors store energy
|
We introduced Potential Energy as an alternative to Force, since it was
a much easier way to handle problems: scalar quantities are easier than vectors.
- For the same reason, we introduce Potential.
-
| The relationship is a bit complicated |
 |
-
Means we can use any results derived for gravitation for electrostatics.
- Just as the zero of P.E. is arbitrary, so is the zero of potential: only differences really matter, so we should really talk about "Potential Difference" or P.D.
-
e.g.
| Simplest case is uniform electric field. Two oppositely charged flat plates: fields will cancel outside them, but
add in between.
We found the field is
\color{red}{
E = 4\pi k\sigma }
so the potential is
\color{red}{
V = - 4\pi k\sigma d = - \frac{{\sigma d}}{{\varepsilon _0 }}}
since the field is a constant in this case. (Exactly the same argument as gravitational PE near the earth's surface). Minus sign arises since we define
\color{red}{
U = - \int {\vec F.d\vec s} }
|
|
| In this case the flow chart becomes much easier. (remember, E is a constant) |
 |
- Unit for V is Volts (which is why E is measured in Volts/metre).
- We will often refer to potential as "voltage" which is sloppy but useful.
The potential for a single point charge comes from Coulomb's law:
\color{red}{
E = \frac{{kq_1 }}{{r_1 ^2 }} \Rightarrow V = \frac{{kq_1 }}{{r_1 }}}
(k = 9x109 N m² C-2as before.)
We can use potential as we used PE: e.g.
- What is the potential at a distance of 15 cm from a 3 μC charge?
- How much work would we have to do to move a 1 μC charge from ∞ to a distance of 15 cm from the 3 μC charge?
- Just as with P.E., we can go from potential to K.E.
- e.g. a TV set has a P.D. between the cathode at the back and the screen of 30,000 V. How fast are the electrons moving when they hit the screen?
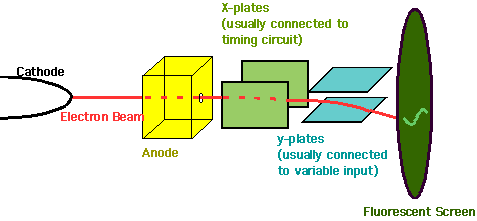
The Oscilloscope
the most useful scientific instrument in existence.
Allows any time dependent
quantity which can be converted into an electric signal to be measured.
e.g
- Sound
- Nerve Impulses
- Signals in circuits
- Radio signals from Space (SETI)
- Cathode is usually at ~-10 kV, anode at 0 V.
- Deflection at X- and Y- plates
is controlled by voltage (i.e. charge) on them.
- This is the basic technology
of the (old-fashioned!) TV: however there the steering of the beam is done (partly) by mag. fields.
|
 |
Some important special cases of potential:
| Potential due to a dipole (two equal and opposite charges).
|
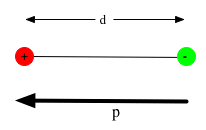 |
- The total charge is zero, so would expect this to vanish at large distances.
- Just as with fields, can add potentials
\color{red}{
V_ + = \frac{{kq_{} }}{{r_ + }},V_ - = - \frac{{kq_{} }}{{r_ - }},r_ \pm = r \mp \frac{d}{2}}
-
- Hence
\color{red}{
V = V_ + + V_ - = \frac{{kq_{} }}{{r_ + }} - \frac{{kq_{} }}{{r_ - }} \approx \frac{{kqd}}{{r^2 }}}
- Note that pot. due to a single point charge ∝ 1/r: for a dipole V ∝ 1/r² .
What do we get off axis (i.e. at an angle θ to the direction of the dipole)?
\color{red}{
V = \frac{{kqd\cos \left( \theta \right)}}{{r^2 }}}
What does this mean
- at θ = 0
- at θ = π/2
- at θ = π
| e.g a hollow sphere: field E = 0 inside,
exactly like a point charge outside.
\color{red}{
E\left( {\vec r} \right) = \left\{ {\begin{array}{*{20}c}
{0\left( {r < R} \right)} \\
{\frac{{kq_1 }}{{r^2 }}\hat r\left( {r > R} \right)} \\
\end{array}} \right.}
|
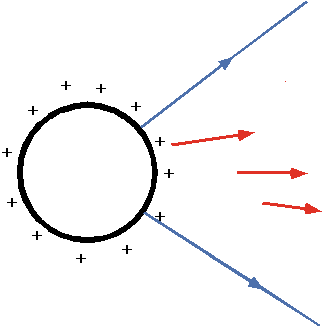 |
- However, inside the field is zero, so this gives a constant potential inside
\color{red}{
V\left( r \right) = \left\{ {\begin{array}{*{20}c}
{\frac{{kq}}{R}\left( {r < R} \right)} \\
{\frac{{kq}}{r}\left( {r > R} \right)} \\
\end{array}} \right.}
(a potential must always be a continuous function) |
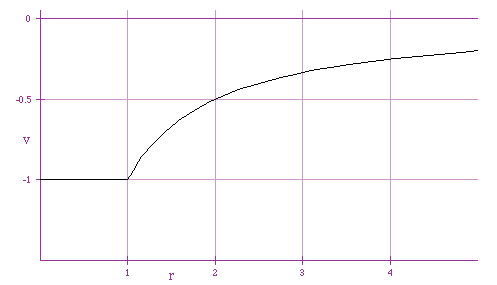 |
Note that we have usually said the the zero of potential is arbitrary: however
here we have defined the cathode to be at -30 kV and the anode (and screen) at
0 V. It would work equally well with the cathode to at 0 kV and the anode (and
screen) at +30 kV. Why don't we do this?
- It is just a convention, chosen by the manufacturers
- The potential is measured with respect to the outside world, so + 30 kV would
tend to fry small kids who were at 0 V.
- It is much easier to produce large negative voltages, since electrons are
easier to move that protons.
Potential ⇔ Field
As with P.E. and force, we can go from potential to field. Formally
\color{red}{
E = - \frac{{dV}}{{dx}}}
This means (for a linearly increasing potential),
|E| = V/d
We can have problems getting the sign of the PE correct:
Sign of work done and potential.
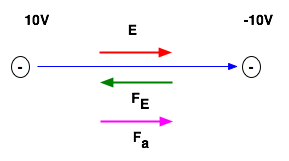
e.g. an electron is moved from a place where the potential is 10 V to where it is -10 V. What is the work done by the external applied force?
- Answer: the potential is decreasing.
E = - dV ≈ - δV
dx δx
so E is positive.
- Hence if we were moving a + charge, F and E are in the same direction and the W.D. would be positive.
-
In this case the charge is -, so F and E are in opposite directions, so the W.D. is qδV = -3.2*10-18 J.
- However this is the W.D. by the electric field: you have to supply a force in the opposite direction, so the W.D. = 3.2*10-18 J.
-
To visualise this might be to think of charged plates as producing the field.
Why didn't we talk about gravitational field and gravitational potential when we dealt with gravity?
-
We could have, but it doesn't help us very much, because
- There is only one sign for the grav. field.
- Grav. field doesn't get distorted by other materials.
However, the "Fluid Analogy" is useful:
- It is useful to have an analogy for charge, field, potential and capacitance (and everything else electrical)
- Charge ~ water
- Potential ~ gravitational P.E. of water (think of a dam) ~ height above sea-level
- Field ~ force that would act on the water if it was on sloping ground
- Don't take this too seriously (we don't have negative water!) but it sometimes helps, for example with
Equipotentials
Surfaces of constant electric potential.
| For a point charge
Note that the equipotential surfaces must always be perpendicular to the field lines |
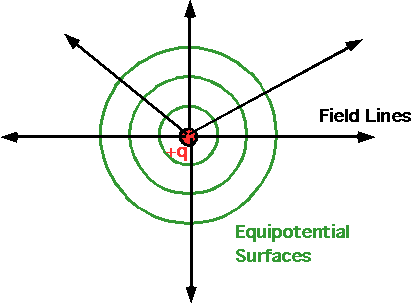 |
- Why?
- Think of the work done in carrying a bucket!
What are the equipotential surfaces called in geography?
The equipot. surfaces get more complicated with more charges:
| e.g. a dipole |
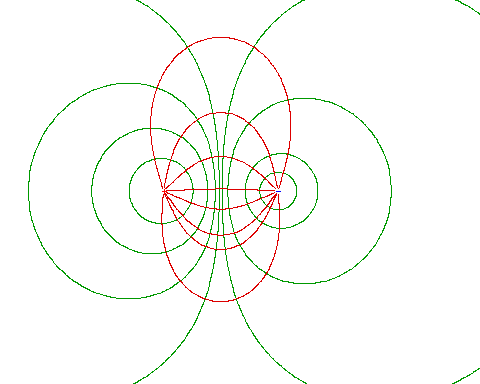 |
| The 3 charges that we consider earlier |
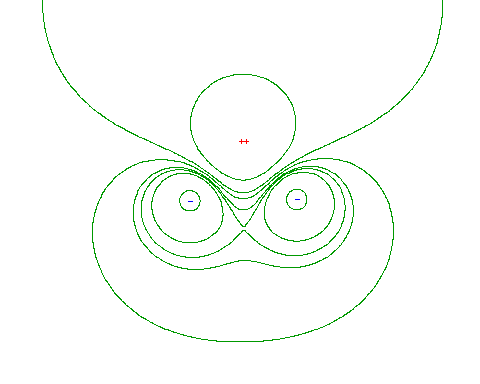 |
| even in this case the equipots are perp to the field lines |
 |
| Obviously the parallel plate system has equipots (almost) || to the plates |
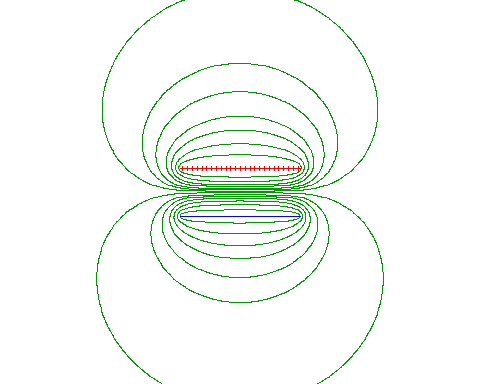 |
Conductors and Insulators
The surface of a conductor is always an equipotential.
| If it wasn't then there
would be an electric field acting on any charges, given a force so the charges
would move so as to make it an equipotential.
Also the inside of a conductor is an equipotential. |
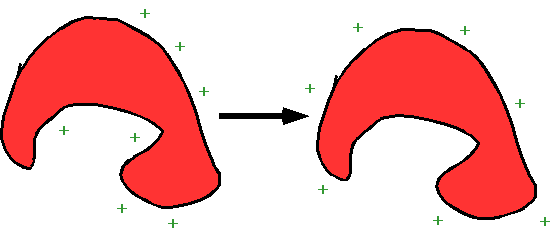 |
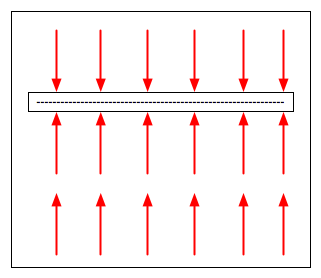
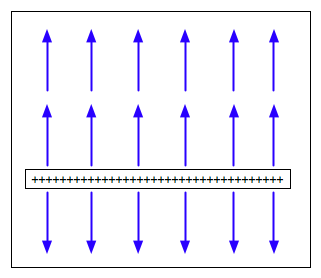
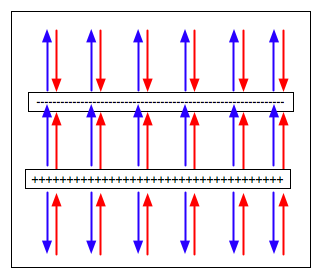
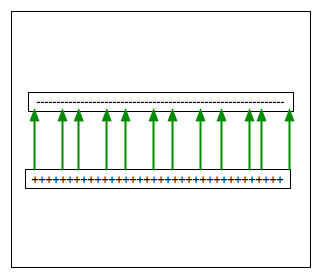
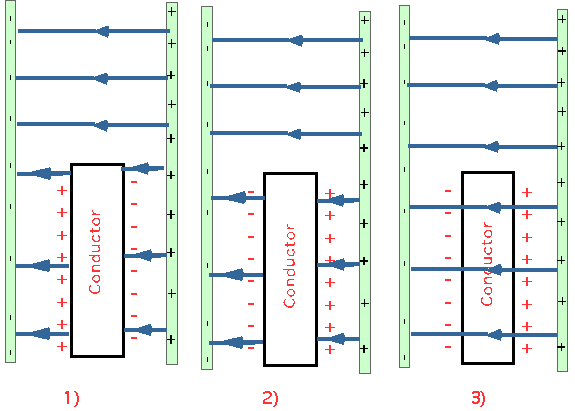
A conductor is put between two charged plates.
| Which of the
diagrams shows the charges and fields correctly? |
 |
Insulators can't do this:
| However, insulators often consist of dipoles, |
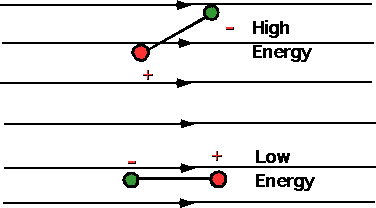 |
| and
these dipoles can be lined up by a field. |
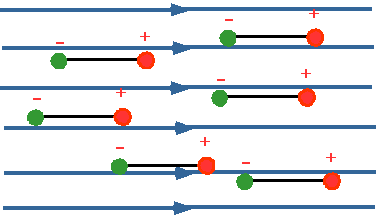 |
| So we can get small charges induced on the surface |
 |
| If these are part of a solid, the charges on the dipoles
will cancel out inside the solid, but add up on the surface |
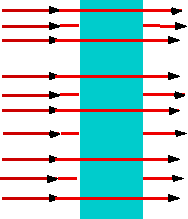 |
- This kind of insulator (which means almost all of them) is known as a dielectric.
- The net effect of dielectric is to reduce the electric field inside, but not
to zero.
-
Breakdown voltage:
Reality raising its ugly head again!
We have treated field, charge and potential as if they can be adjusted arbitrarily. However, there is a maximum field in any material
- When
an electric field is applied to a molecule, a dipole will be induced (electrons move up the field). There are always
- some free electrons...
- accelerated by the field
- which collide with atoms with sufficient energy to knock off electrons...
- accelerated by field...
- collide with atoms....
- This is avalanche process ⇒ spark.If the field is too low, the electrons
will not pick up enough energy in the gap between atoms to ionize them.
- Critical
field Emax for air is ~ 106 V m-1:
- for most solids ~ 107 Vm-1.
- Why
would we expect it to be higher for a solid?
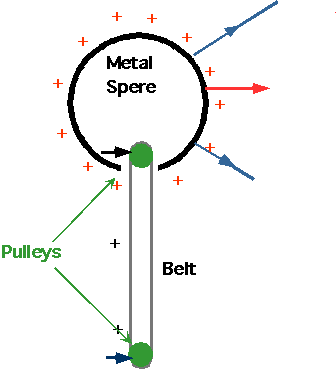
The Van de Graaf generator.
| The belt transfers
charge at a very low voltage to the sphere: repulsion between the charges forces
them to sit on the exterior of the sphere. Maximum voltage is given by
\color{red}{
\left. {\begin{array}{*{20}c}
{E_{\max } = \frac{{kQ}}{{R^2 }}} \\
{V_{\max } = \frac{{kQ}}{R}} \\
\end{array}} \right\} \Rightarrow V_{\max } = RE_{\max } }
|
 |
What would the maximum voltage be on a Van der Graaf generator
if the sphere is 40 cm in radius, and the breakdown field in air is 3x106
Vm-1?
- 1200 V
- 1.2x104 V
- 1.2x106 V
- 1.2x108 V
What would the charge on a Van der Graaf generator
if the sphere is 40 cm in radius, and the breakdown field in air is 3x106
Vm-1?
- 53 µC
- 533 µC
- 5330 µC
- 5.33 C
A thunderstorm:
| works a bit like a Van der Graaf: positive charge is carried up by the up-drafts. Can
get charges up to 100 C. |
|
 Lightning
Photo by Gary Barnhart/Colorado
|
What would be the field
at the ground in a thunderstorm,m if the base of the cloud,
with the charge 0.3 C, has an area of 104 m²
- 3.4 Vm-1
- 3400 Vm-1
- 3.4x104 Vm-1
- 3.4x106 Vm-1
| The cloud will induce an equal and opposite charge on the ground. |
 |
What should you do if you are out on a lake in a canoe and a thunderstorm hits?
- Get into the water as fast as possible
- If you are in a aluminum canoe, get into the water as fast as possible
- If you are in a fibreglass canoe, get into the water as fast as possible
- Stay where you are and lie down
Electric Fish
An interesting example of applications of electric fields:
if you are a fish and youi live in a muddy river, how do you see things?

| You make a dipole field |
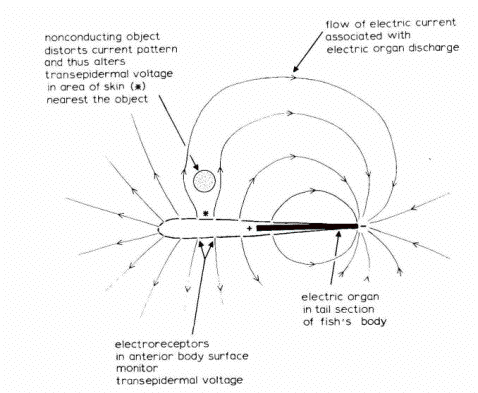 |
Due to André Longtin , University of Ottawa and collaborators
Capacitance
FInal application of static electricity is Capacitors
Parallel Plate system: There is another way of writing the eqn. for the parallel plates:
V= 4πkσd
- and
σ = Charge = Q
Area A
- so
Q = A
V 4πkd
|
 |
This tells you that if you put a certain amount of charge on parallel plates,
there will be a certain fixed voltage.
- This is known as the capacitance.
C = A = ε₀A
4πkd d
- We can
define the same quantity for a spherical conductor:
-
V = -kQ
R - (this is the P. D. between the surface of the sphere and ∞) so that
-
C = Q = r
V k
Capacity is measured in farads (which is an enormous unit)
What is the capacity of the earth? (R = 6500 km), assuming it is a conducting sphere.
- 720 f
- .72 f
- 7.2x10-4 f
- 7.2 μf
Charge as a fluid.
It's a bit hard to visualize capacitance: it helps to think of charge as a fluid.
- Charge ~ water
- Potential ~ gravitational P.E. of water (think of a dam) ~ height above sea-level
-
| Capacitance ~ volume of a bucket to hold the water |
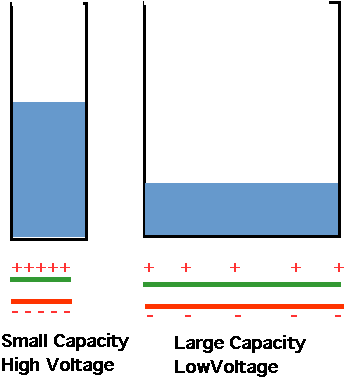 |
- (e.g.) a small capacitance needs a much larger voltage to hold a given charge
than does a large capacitance.
Dielectrics
Usually a solid material is put between the plates of a capacitor: this has the effect of reducing the field for a given charge (the dipoles get rotated).
Dielectric constant
K = Eapplied
Eeff
This
- increases the capacitance:
C = KA = Kε₀A
4πkd d
e.g. for air, K ~ 1.0006, for glass K ~ 10, for water K ~78.
- increases the breakdown voltage
- physically separates the plates (note there is an attractive force between them, so they must be held apart)
| An application of this: the proximity detector. By measuring the capacitance, (via the voltage) can decide if a dielectric object has entered. |
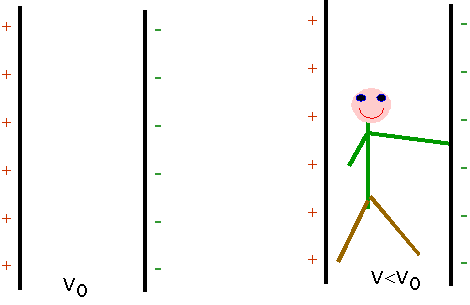 |
| Can even do this by regarding object as one plate of capacitor |
 |
| Another demonstration of the same effect (Thank you, Andrew Schagen!): the wahprobe |
|
.
Energy in capacitors:
We can store energy in capacitors
Work done in adding charge dQ is V dQ, but V = Q/C, so
U = ½CV²
|
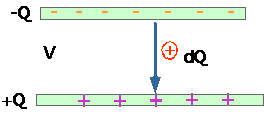 |
(Same calculation as we did for P.E. stored in stretched spring).
e.g an inventor proposes to build a car where the energy is stored in a parallel plate capacitor with a area of 100m², separation d = 10μ, dielectric constant K = 10.
- What is the capacitance?
- What is the maximum voltage? (take the breakdown field to be 3x107 V m-1
- How much energy can be stored?
- Would you invest in it?
Energy Density
e.g. Assume that you are trying to store energy at the same density as in gasoline: what field E would you need? (1 litre [~10-3 m³]~ 4x107 J), ε₀ = 8.85x10-12 C²N-1m-2 or k = 9x109 N m² C-2.
- 105 V/m
- 107 V/m
- 109 V/m
- 1011 V/m
So why do you use capacitors to store energy? Energy can be released very rapidly, but non-destructively. e.g. flash for camera has all of energy released in ~ 1 ms.
| An example of energy storage in capacitors. This uses a 27 mF capacitor charged to 4 kV: how much energy does this correspond to? |
|
This sets up electrostatics: we now want to go on and look at current electricity