PHYS1008 Electric Forces and Fields

Outline and objectives:

To understand the origin of electric forces
To be able to relate electric force and electric field
To be able to visualise the electric field
To be able to apply the electric field in simple situations
To calculate the electric field for a few geometries

History

Historically: very hard to study electricity. Until 18th Century, all experiments were done with magnetism (which is easy to do, but even harder to understand!).

(picture from L. Taylor, Univ. Maryland)

This shows you the kind of experiment that was done

Franklin, Priestly, Coulomb and others found:

Electricity came in two kinds (resinous and vitreous) which we now call
positive and negative charges.
Some materials allow charge to move around (conductors)
Some materials will hold a charge, but do not allow it to move (insulators)
Like charges (++ and --) repel, unlike attract (+- and -+).
Now know that charge is conserved, smallest unit of charge is that on electron (or proton)
SI unit is Coulomb, which is a huge amount of charge.
Charge on electron q = -1.6x10^-19 C

Coulomb's law:

inverse square law, like gravitation

\color{red}{ F_G = \frac{{Gm_1 m_2 }}{{r^2 }} \Rightarrow F_E = \frac{{kq_1 q_2 }}{{r^2 }}}

k is just a number (like G): k = 9x10⁹ N m² C^-2, charge is measured in coulombs

Most more advanced books use

k = 1  
   4πε₀

where

ε₀ = 8.85x10^-12 C²N^-1m^-2

Reason is that more important equations are simpler written in terms of ε₀

How do we apply this?
e.g. What is force between 2 charges of 5 μC, separated by 20 cm?

An interesting comparison: electric and gravitational forces have exactly the same 1/R² dependence:
what is the ratio of the electric and gravitational forces between two electrons?
\color{red}{ \frac{{F_E }}{{F_G }} = \frac{{kq_1 q_2 }}{{r^2 }}\frac{{r^2 }}{{Gm_1 m_2 }} = \frac{{kq_1 q_2 }}{{Gm_1 m_2 }}}
~ 4.2 *10⁴²
(Hitchhiker's Guide fans please note!). Why is this ratio so large?
We don't know!

If the electrostatic force is so much stronger than gravity, why don't we feel it?

Everything we are made of is neutral, so there are no electrostatic forces
We consist of an equal number of positive charges (protons) and negative (electrons), so the forces cancel out
Everything on the earth has a small negative charge and the earth has a positive one, so we are attracted to it for this reason

Since F is a vector we need to be careful about directions

\color{red}{ \vec F_{12} = \frac{{kq_1 q_2 }}{{r^2 }}\hat r_{12} }

where \color{red}{\vec F_{12} } is the force of charge 1 on charge 2, and \color{red}{\hat r_{12} } is the unit vector that points from 1 towards 2.

What does Coulombs law mean?
Imagine we have a single fixed charge, and some moveable ones that we can use to measure the force (this is the experiment that Coulomb would like to have done!). a single point charge

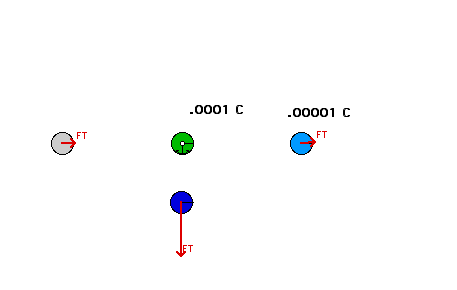The charge on the green ball is 10^-4 C, and the charge on the light blue ball is 10^-5 C. The magnitude of the forces are 0.25N? What is the charge on the grey ball?

10^-5C
10^-4C
-10^-5C
-10^-4C

The magnitude of the force on the dark blue ball is 1.0N? What is the charge on it, if its distance from the green ball is half that of the light blue ball?

10^-5C

10^-4C

-10^-5C

-10^-4C

Superposition

Can add the field due to several charges: for example a case with two equal charges. This is known as "superposition". This shows how it works for a dipole

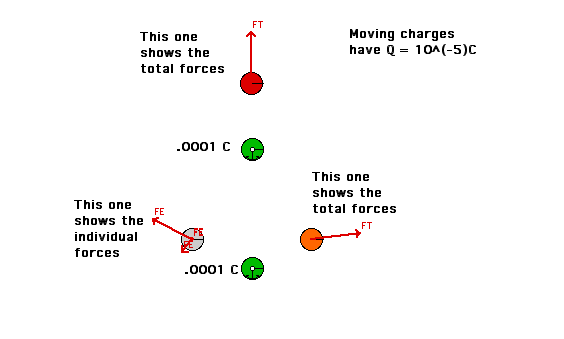The charge on the green ball is 10^-4 C, and the 2 grey balls have the same charge of 10^-5 C. What is the charge on the white ball?

10^-5C
10^-4C
-10^-5C
-10^-4C

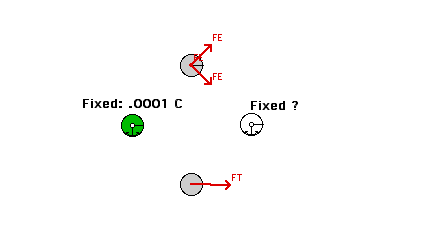Induction

We can measure charges with a an electroscope:

Can charge a body without actually touching it with a charged one

e.g. charging by induction

Conductor is neutral
Charged object separates charges on conductor
Earthing conductor allows charges to escape
...leaving negatively charged conductor

Electric field

There is "something" that exists whether or not we measure it:
this "something" is field.
The relation between the force and field:
```
F = qE 
```
Unit for E is Newtons/Coulomb,
and (exactly the same thing) Volts/metre.
We can measure the force at a whole lot of places with a test charge:
For example, a single point charge
or a dipole

Lines of Force/Field Lines

We can also arrange out test charges to sketch out the field.

If we arrange the charges so that the force vectors line up, we get a diagram that draws out lines: these are known as "field lines" or "lines of force". Drawing these lines of force helps us to visualize what will happen to a charge in an electric field.

Rules for drawing lines of force:
Lines start from positive charges
Lines end on a negative charge
Lines cannot cross (why)
Close to a charge, lines go radially outwards (or inwards)
density of lines represents (roughly) strength of field
e.g. a dipole

Franklin http://my.vbe.com/~ppeters/franklin.html lets us visualize the field: e.g.

2 positive charges
Is there a place where we can put a charge so it does not feel a force?
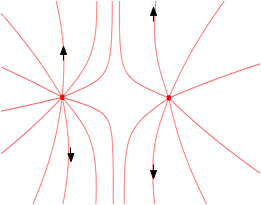More complicated examples:
charges arranged in a triangle

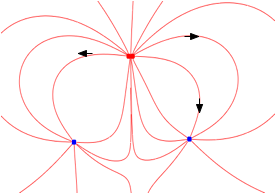Note that if charges don't "cancel out", some lines will go to infinity

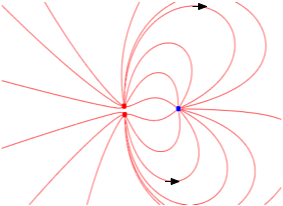and looked at from large distance, they will look almost like one point charge

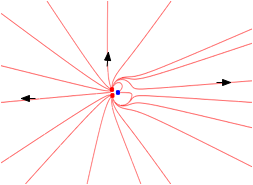Adding Fields

However, we need to be able do this quantitatively: i.e. we need to be able to add the effect of several charges Some important special cases of electric field:

Point charge (obviously!):

\color{red}{ F = k\frac{{q_1 q_2 }}{{r^2 }} \Rightarrow E = k\frac{{q_1 }}{{r^2 }}}

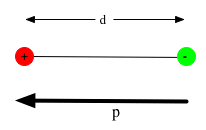
Field due to a dipole (two equal and opposite charges). The total charge is zero, so would expect this to vanish at large distances. It almost does!

\color{red}{ E = 2k\frac{{qd}}{{r^3 }}}

Dipole FIeld

On-axis proof: \color{red}{E = \frac{{kq_1 }}{{r_1 ^2 }} + \frac{{kq_2 }}{{r_2 ^2 }}}

can simplify \color{red}{ = kq\left( {\frac{1}{{\left( {x + \frac{d}{2}} \right)^2 }} + \frac{{ - 1}}{{\left( {x - \frac{d}{2}} \right)^2 }}} \right)}

so that \color{red}{E \approx \frac{{2kqd}}{{x^3 }}} We have used superposition here

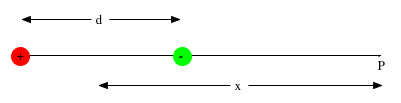If we don't make the large distance approximation, we get this. Note that the field is most intense (lines are densest) near the charges

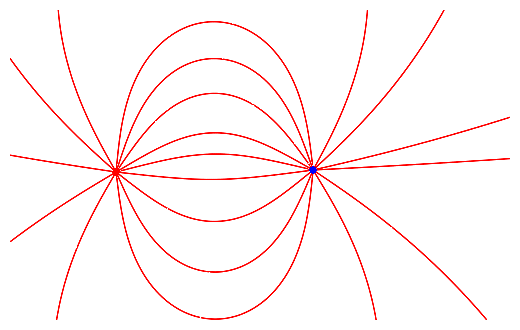Why do we use Electrostatic Fields? We can use the field to visualize what will happen to a charge.

What is the direction of the force on an electron in a uniform field?
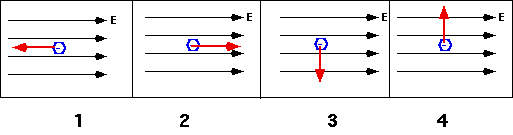An electron is at rest in a field of 1000 V/m.
1. What is its acceleration?
2. How long does it take before it is travelling faster than the speed of light?
3. Why is the calculation silly?

e.g. many molecules (such as water) act as tiny dipoles : they are overall neutral, but consist of two (or more) charges separated by a small distance. Dipole moment \color{red}{\vec p = q\vec a} , direction from negative to positive

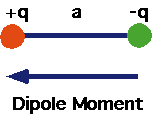An electric dipole is in a uniform electric field. What will happen to it?

It will move to the left.
It will move to the right
It will rotate counter-clockwise
It will rotate clockwise

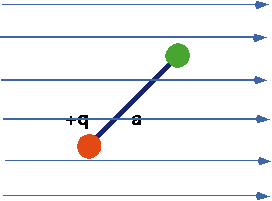Quantitatively:

if there is a dipole \color{red}{{\vec p}} in a uniform field \color{red}{{\vec E}}
the torque will be \color{red}{\left| {\vec \tau } \right| = Fa\sin \left( \theta \right)}
but \color{red}{\vec F = q\vec E} and qd = p,
so this is \color{red}{\left| {\vec \tau } \right| = pE\sin \left( \theta \right)}
Energy of a dipole:
\color{red}{ U = - pE\cos \left( \theta \right)}
i.e. energy is lowest if cos(θ) = 1, so dipole is aligned with field.
What happens to a dipole in a non-uniform field?

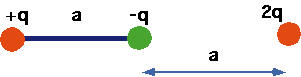
Electrostatic Field Examples

Examples

What is the field at the 2q charge?
What will the force on the 2q charge be if a = 5 cm, q = 2 μC?
How would the force change if the 2 q charge was moved to the equivalent point on the other side of the dipole?

It is quite a bit harder to do this if we have charges away from a line, because we then need to add up vectors.
e.g. What is the field at the origin given the following arrangements of charges? What does the field look like? Is there any place where a positive charge would feel no force?

Continuous Charge Distributions

Usually we don't have single charges: charge is spread out on in a line or a surface:

e.g. charged flat plate: if the total charge is Q, and the area is A, then \color{red}{\sigma = \frac{Q}{A}} is the charge/unit area. The field is given by
\color{red}{ E = 2\pi k\sigma = \frac{\sigma }{{2\varepsilon _0 }}}
Note what this means: the field is independent of the distance from the plate. In fact his is only true if the distance from the plate is small compared to the size.
Field is constant (almost). More exactly, the centre of a disk with a uniform positive charge the electric field points away from the disk and is nearly constant in magnitude;

This is for an infinite flat plate: in reality for a finite disc:

QuickTime plugin needed for this movie.

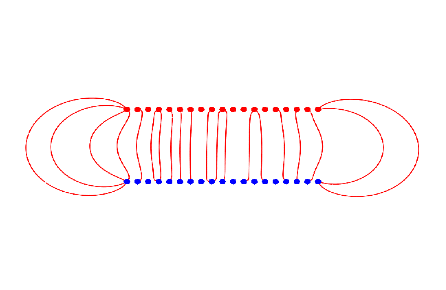
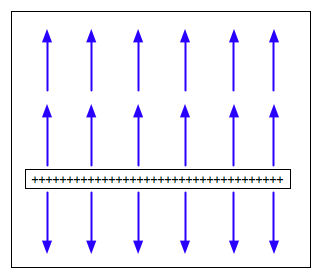
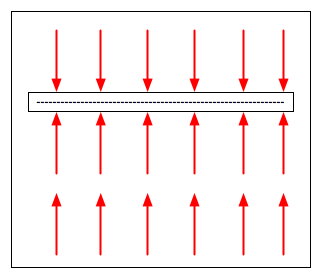
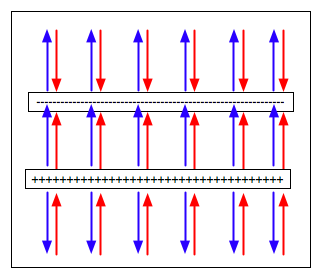
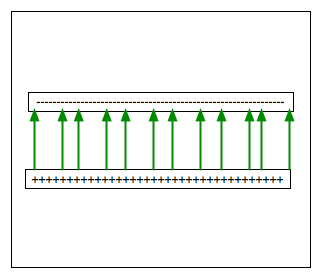
Two flat plates

Very Important.

Two oppositely charged flat plates: fields will cancel outside them, but add in between.

giving \color{red}{E = 4\pi k\sigma = \frac{\sigma }{{\varepsilon _0 }}}

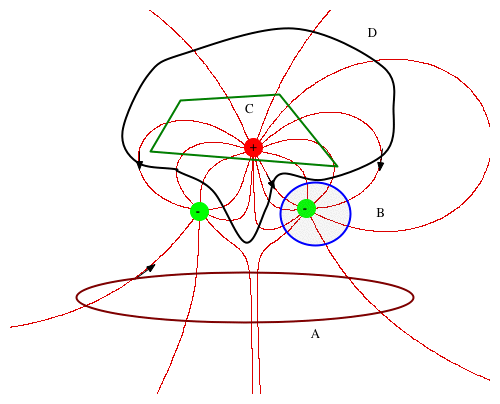
Gauss' Law

If we draw a surface round a bunch of charges, the total # of lines of force crossing the surface is the same. (note we have to count lines going in as negative).

If the number of lines of force from a given charge is taken to be the same, we can measure the total charge by counting the lines of force.
e.g. our old example with charge + 2 and 2 charge -1: How many lines of force pass through the surface

A
B
C
D

Formal way of stating this is Gauss' law: define flux φ of E through the surface (misleading, since nothing flows!).

\color{red}{ \phi = E_ \bot A = EA\cos \left( \theta \right)}

This gives the total charge inside

\color{red}{ \phi = 4\pi kq = \frac{q}{{\varepsilon _0 }}}

This says: At every point of the surface, find the field, take the component of E ⊥ surface and add these up: the result is ∝ charge inside

Units of flux: [E] Vm^-1, so [φ] = Vm.

Sign of flux: for a closed surface, count it as positive when vector E points out.

Meaning of φ What is it in these 3 cases?

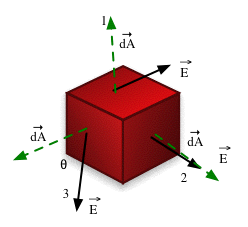What is φ in case 1?

What is φ in case 2?

What is φ in case 3?

0
EA sin(θ)
-EA sin(θ)
EA cos(θ)
-EA cos(θ)

Gauss' Law is always true, but only useful if we can fix things so that either \color{red}{\cos \left( \theta \right) = 0} or \color{red}{\cos \left( \theta \right) = 1} and E is a constant. We need some symmetry in the problem to do this. What does symmetry mean? In this context it means: if we have a charge distribution which gives rise to a field, then if we can move in such a way that the source looks the same, then E will be the same.

Suppose we have a charged cone, as shown. We can move it along the z-axis (a translation), or rotate it about the z-axis (a rotation). Do we expect E to be the same under

both translations and rotations?
translations but not rotations?
neither?
rotations but not translations?

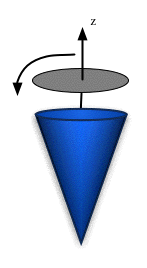
e.g point charge, draw a sphere, radius R: E is the same at any point,

\color{red}{ \phi = E_ \bot A = EA = E4\pi r^2 }
and
\color{red}{ \phi = 4\pi kq = \frac{q}{{\varepsilon _0 }}}
\color{red}{ E = k\frac{q}{{r^2 }}}
But we knew this!

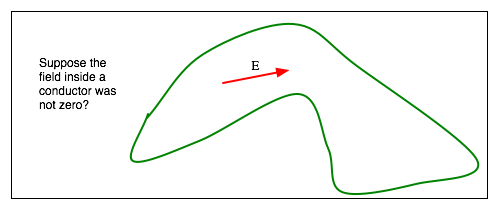
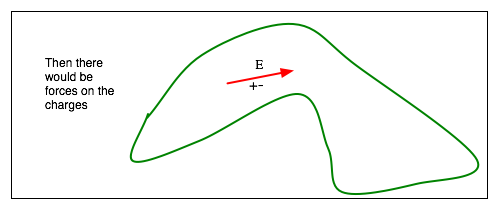
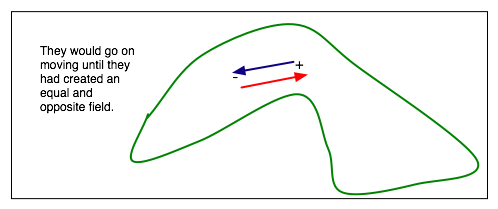
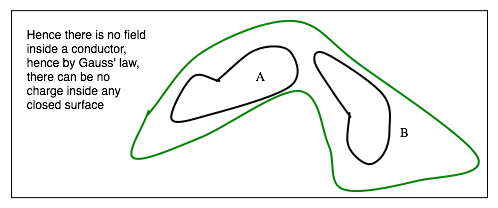
Field inside a conductor?

Hence if there is a charge on a conductor, it must be on the surface.

Line Charge

Charge/unit length = λ

Similar argument: Field must be constant and ⊥ surface. Make the Gaussian surface a cylinder: charge contained in the surface is \color{red}{q = \lambda l}
E only passes thorough cylinder, so that flux
Hence \color{red}{E = 2k\frac{\lambda }{r}}

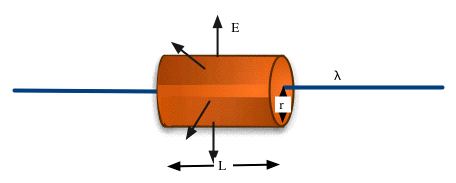Hollow Sphere:

Charge entirely on the surface: draw Gaussian surfaces as shown.

No charge inside, so E = 0
Outside, spherical symmetry, so exactly like a point charge

\color{red}{ E\left( r \right) = \left\{ {\begin{array}{*{20}c} {0\left( {r < R} \right)} \\ {\frac{{kq_1 }}{{r^2 }}\left( {r > R} \right)} \\ \end{array}} \right.}

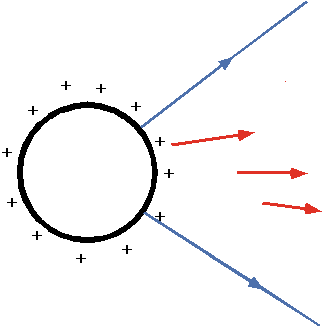Thre are a few situations (like the hollow sphere) where we need the field, but it's very hard to calculate directly. It is usually much simpler to use potential than work directly with fields.