1008 Electric Capacitance

By the end of this you should understand the following the basic idea of capacitance how to calculate it in simple cases. how capacitors store energy how capacitors work in circuits

Capacitance

FInal application of static electricity is Capacitors

Parallel Plate system: There is another way of writing the eqn. for the parallel plates: V= 4πkσd and σ = Charge = Q Area A so Q = A V 4πkd

• This is known as the capacitance.

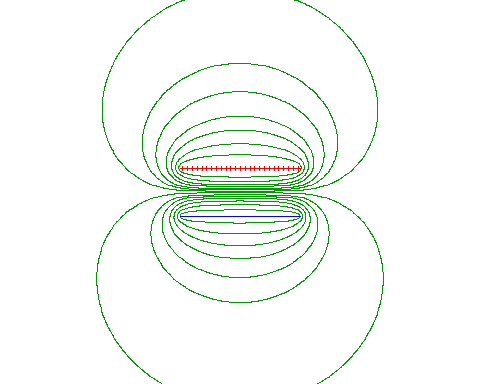  C =  A  = ε₀A
     4πkd    d
  

• We can define the same quantity for a spherical conductor:

• V = -kQ
        R

• (this is the P. D. between the surface of the sphere and ∞) so that

• C = Q = r
      V   k

What is the capacity of the earth? (R = 6500 km), assuming it is a conducting sphere.

1. 720 f
2. .72 f
3. 7.2x10^-4 f
4. 7.2 μf

Charge as a fluid.

• Charge ~ water
• Potential ~ gravitational P.E. of water (think of a dam) ~ height above sea-level

• Capacitance ~ volume of a bucket to hold the water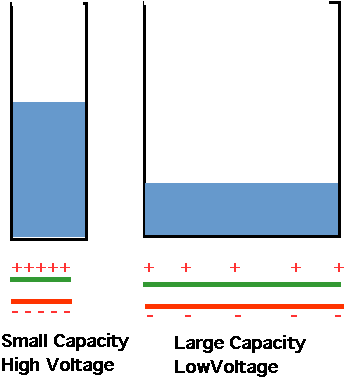

• (e.g.) a small capacitance needs a much larger voltage to hold a given charge than does a large capacitance.

Dielectrics

Usually a solid material is put between the plates of a capacitor: this has the effect of reducing the field for a given charge (the dipoles get rotated).

Dielectric constant

K = Eapplied
    Eeff

• increases the capacitance:

  C = KA  = Kε₀A
     4πkd    d
  

  e.g. for air, K ~ 1.0006, for glass K ~ 10, for water K ~78.
• increases the breakdown voltage
• physically separates the plates (note there is an attractive force between them, so they must be held apart)

An application of this: the proximity detector. By measuring the capacitance, (via the voltage) can decide if a dielectric object has entered.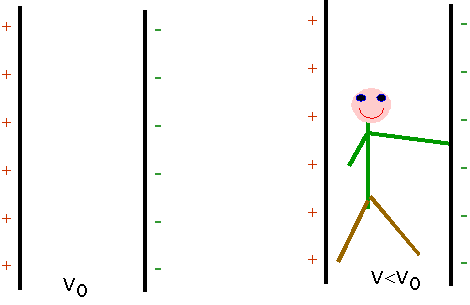
Can even do this by regarding object as one plate of capacitor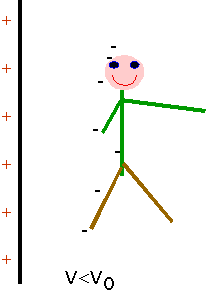

Energy in capacitors:

Work done in adding charge dQ is V dQ, but V = Q/C, so U = ½CV²

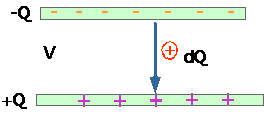(Same calculation as we did for P.E. stored in stretched spring).

1. What is the capacitance?
2. What is the maximum voltage? (take the breakdown field to be 3x10⁷ V m^-1
3. How much energy can be stored?
4. Would you invest in it?

Energy Density

• If we have a parallel plate capacitor, the energy is given by

  U = ½CV² and C = ε₀A and V = Ed  
                    d

• gives energy density

  u = U/Volume  = ½ε₀E² = ½E²/4πk
  

  Note that this holds in general for any electric field

1. 10⁵ V/m
2. 10⁷ V/m
3. 10⁹ V/m
4. 10¹¹ V/m

An example of energy storage in capacitors. This uses a 27 mF capacitor charged to 4 kV: how much energy does this correspond to?

Capacitors in Circuits:

We frequently need to combine capacitors with other electrical components: the symbol is obvious!

SImplest possible is just a capacitor and battery (in paractice always have an resistance). Can assume that battery just applies constant voltage.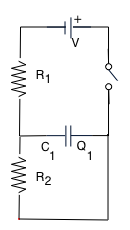

Combinations of capacitors

Practical circuits often combine different elements, such as resistors, capacitors and inductances (and "active" elements like transistors etc). Hence we need to know how to combine them. e.g.

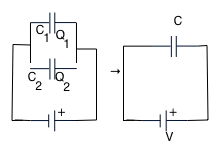
In parallel: we want to replace 2 capacitors by a single equivalent one: in this case that must have the same voltage across each one, so Q₁ = V C₁, Q₂ =V C₂, Q = VC but Q₁ + Q₂ = Q so that C = C₁ + C₂ this is almost obvious, if we think of C₁ and C₂ as being part of a larger cap. C.

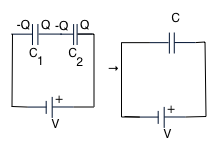
In series: in this case the central part is isolated and neutral, so charges must be +Q and -Q as shown. Hence V = V₁ + V₂ = Q = Q + Q C C₁ C₂ so that 1 = 1 + 1 C C₁ C₂

Useful to remember that this is the opposite of the corresponding relations for resistors.

e.g suppose C₁ = 1 μf,C₂ = 2 μf, C₃ = 12 μf, what is the equivalent capacitance of the circuit?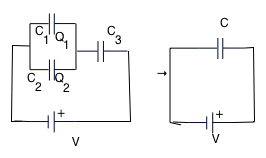

This sets up electrostatics: we now want to go on and look at current electricity