Celestial Mechanics

Outline:

Universal Gravitation + Mechanics ==>

The fundamental relations:

Except that now we want to have two bodies moving under mutual gravitation, so that force of m2 on m1 is

Define Relative and Centre of Mass variables

By differentiating these, we can get the C.o.M. and relative velocities and accelerations

C.o.M motion can be eliminated immediately:

so that A = 0 (no c.o.m. accn.).

Relative motion:

This contains all of the laws:

Third Law for circular orbits is described before:

This has two changes from Kepler: a) We know the constant (what is the mass of the sun) b) the mass is the total mass of the system (not just the sun)

2nd Law: Take � product with r

i.e. Angular momentum doesn't change: L=const

What does this have to do with 2nd. Law?

Area of triangle = 1/2 r v dt, so if dt is fixed, A = 1/2 L = constant m

Conservation of energy: Take dot product with v:

Can combine these to give...

Energy is a conserved quantity

Ist Law: split into tangential and radial components

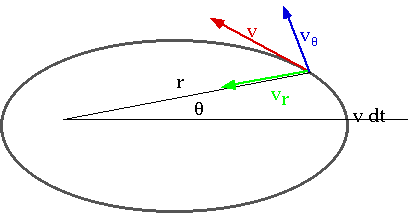
So we can write the energy and ang mom. conservation laws in terms of the new variables:

We now need to combine the last 2 eqns and energy conservation to give us..

This is correct, but not very interesting: to get the shape of the orbit, we need to divide the last two equations

{{ Warning: need links for"1 st law 2.pict",}}

To solve this is a mess: you need to make the following subst.


and this gives the solution

Comments:

All the conic sections are hidden in this:

  1. e = 0 ==> circle <== E = -G2M2/2J2
  2. 0 ellipse E < 0
  3. e = 1 ==> parabola �E = 0
  4. 1 hyperbola E > 0

The fundamental quanities are J, the angular momentum and E, the total energy. Note that if E > 0, then system is unbound

Energy and virial theorem:

Total energy of moon in orbit = K.E. + P.E.

This result is much more general than the "derivation" suggests..

For any bound system interacting via gravitational forces < K.E. > = -1/2

e.g. how much energy would you get by changing orbit of Mars to that of Earth?

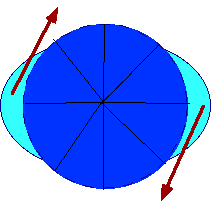
e.g. If a star shrinks, (so that increases) it will heat up (so that increases) and 1/2 the energy must be radiated into space

Tidal Effects:

Newton thought of a) water on near side of earth as being pulled away by moon b) earth being pulled away from water on far side a) + b) gives tides on opposite sides of earth

More accurately, there is a force on every point on the earth, and one must subtract the force on the centre from this.

Note that the effect is really that the water at 900 is pulled flat!

The size of the effect is given by

Note that δr is radius of object, r is the distance from mass. Also note that the Moon is more important than the sun because of the 1/r3

Long term effects of tidal friction:

Friction extracts energy from system, so rotational speed of earth decreases

day decreases by 1/100 s/century

What is energy loss?

ω = 2π/P = 7.27�10-5 rads s-1
so

Hence power consumption

W = dE =  d(1/2Iω2) = Iω dω  =2.5x1017 Watts 
    dt      dt          dt

Can also understand