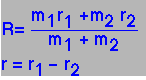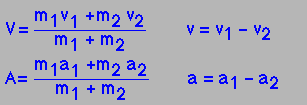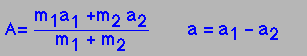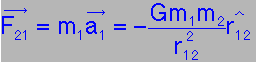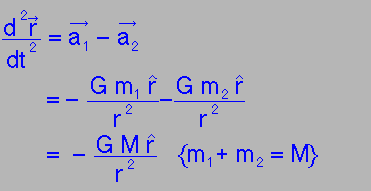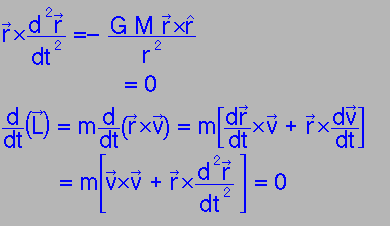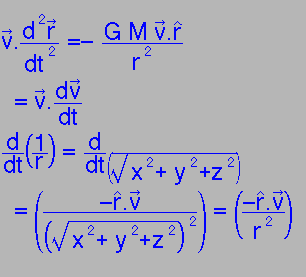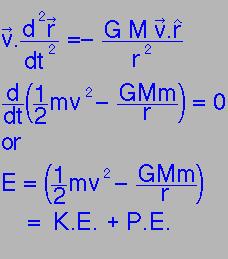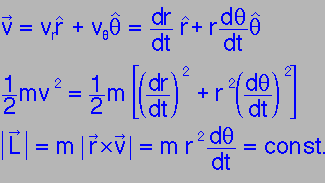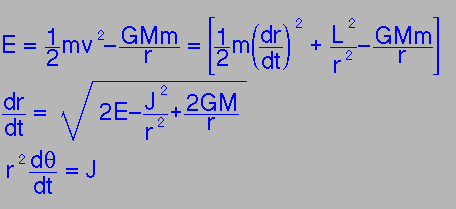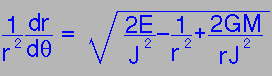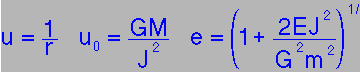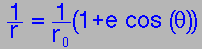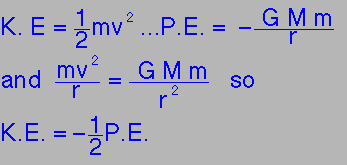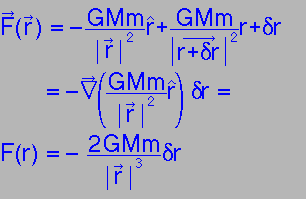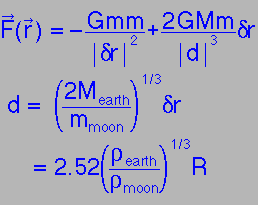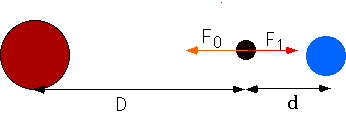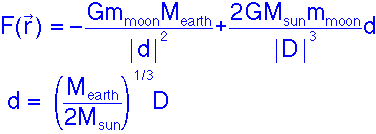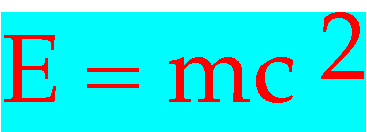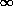Astronomy: Celestial Mechanics
Outline:
Universal Gravitation + Mechanics ⇒
- Keplers 3rd law
- Keplers 2nd law
- Keplers 1st law
- Energy and Virial Theorem
- Tidal forces and Roche's limit
- Stability of orbits
The fundamental relations:
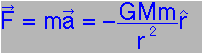 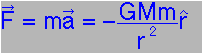 |
The right hand side is shown as a magnitude term multiplying a vector |
But now we want to have two bodies moving under mutual gravitation, so that the force of m2 on m1 is
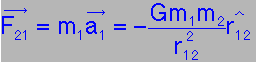 with the changing velocity and acceleration of m1 with the changing velocity and acceleration of m1
due to m2 shown thus: |
 |
| So we define Relative and Centre of Mass variables. |
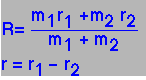 |
where R is the vector for the centre of mass, and r is the vector describing the relative displacement of one body from the other.
| Then by differentiating these, we can get the C.of M. and relative velocities and accelerations. |
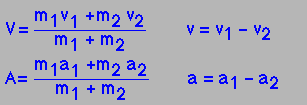 |
|
The C.of M. motion can be eliminated immediately, so that A = 0 (no C.of M. acceleration.). |
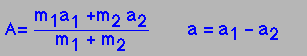 |
and the motion of the bodies follows the pattern shown.
with the motion of the centre of mass shown by the series of X's (ie constant motion, no acceleration).
|
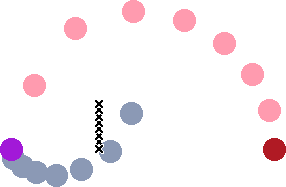 |
| The Relative motion contains all of Kepler's laws: |
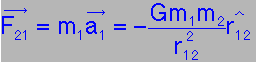 |
Kepler's Third Law.
It is theoretically justified for circular orbits via:
P² = kr³, where for such circular motion, P = 2πr/v
Substituting,
4π²r²/v² = kr³
, or multiplying both sides by mv²/kr⁴ and simplifying:
mv²/r = Centripetal Force = 4π²m/kr² = ma
| Then a is of the form K/r², or from our review of Newton, and the relative acceleration given above: |
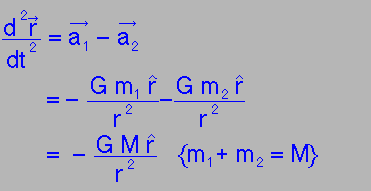 |
This suggests two changes from Kepler's conclusions.
- We know the constant.
- The mass is the total mass of the system (not just the sun)
2nd Law:
Take × product with r
i.e. Angular momentum doesn't change: L=const
|
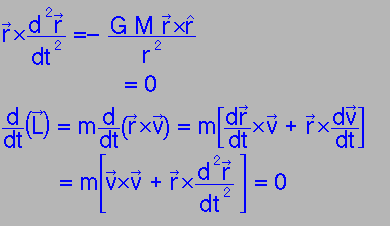 |
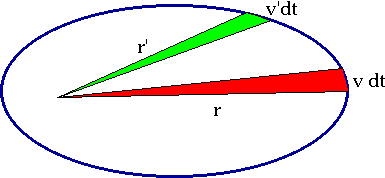
| What does this have to do with 2nd Law? Area of triangle = 1/2 r v dt, so if dt is fixed, A = 1/2 L/m = constant |
 |
Conservation of energy:
| Take dot product with v: |
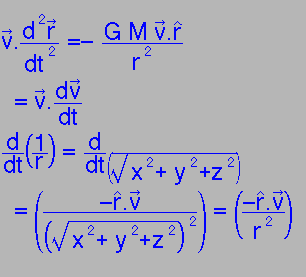 |
Can combine these to give...Energy is a conserved quantity.
|
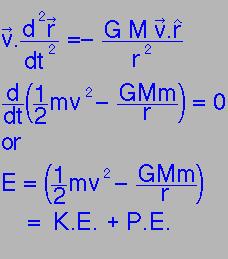 |
1st Law: split into tangential and radial components
|
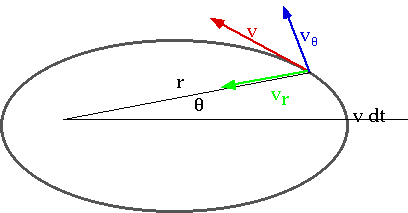 |
So we can write the energy and ang mom. conservation laws in terms of the new variables:
|
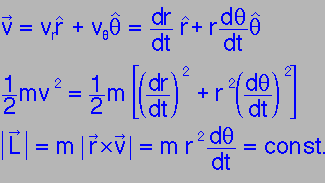 |
We now need to combine the last 2 equations and energy conservation to give us...
|
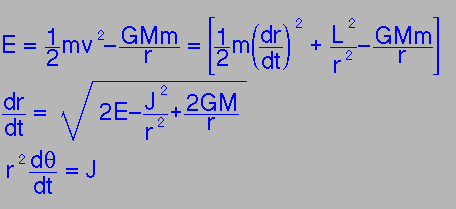 |
This is correct, but not very interesting: to get the shape of the orbit, we need to divide the last two equations
|
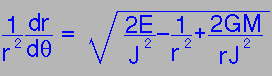 |
| To solve this is a mess: you need to make the following substitution.
|
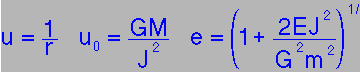 |
and this gives the solution...
|
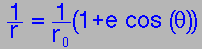 |
Comments:
All the conic sections are hidden in this:
- e=0 ⇒ circle ⇐E = -G²M²/2J²
- 0 <eə ⇒ ellipse ⇐E < 0
- e=1 ⇒ parabola ⇐E = 0
- 1<e ⇒ hyperbola ⇐E > 0
|
 |
The fundamental quantities are J, the angular momentum, and E, the total energy. Note that if E > 0, then the system is unbound.
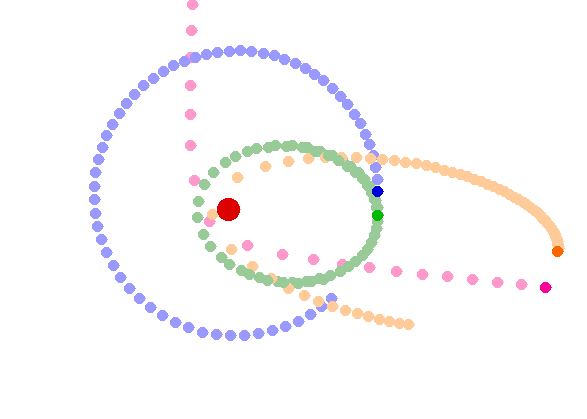
Energy and the Virial theorem
Total energy of the moon in orbit = K.E. + P.E.
|
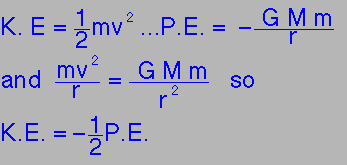 |
This result is much more general than the "derivation" suggests.
For any bound system interacting via gravitational forces
< K.E. > = -1/2 < P.E. >
e.g. how much energy would you get by changing the orbit of Mars to that of Earth?
e.g. If a star shrinks, (so that -< PE > increases towards 0) it will heat up (so that < KE > increases above 0) and 1/2 the energy must be radiated into space.
Tidal Effects:
Newton thought of
- water on the near side of earth as being pulled away by the moon,
- the earth being pulled away from the water on the far side,
- gives tides on opposite sides of the earth.
|
 |
More accurately, there is a force on every point on the earth, and one must subtract the force on the centre from this.
|
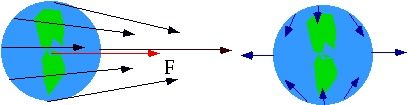 |
Note that the effect is really that the water at ± 900 (with the moon to the right at 00) is pulled flat!
The size of the effect is given by
|
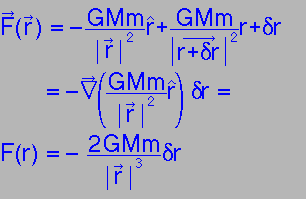 |
Note that δr is the radius of the object, r is the distance from the mass. Also note that the Moon is more important than the sun because of the 1/r³
Long term effects of tidal friction: Friction extracts energy from the system, so the rotational speed of the earth decreases.
The day decreases by 1/100 s/century. |
 |
What is the energy loss?
ω = 2π/P = 7.27 × 10-5 rads s-1
, so
dω/dt = -2π/P² dP/dt = -ω²/2π ΔP/ΔT = 2.67 × 10-21 rad s-2
Hence the power consumption:
W = dE/dt = d(1/2Iω²)/dt = Iω dω/dt =2.5 × 1017 Watts
Angular momentum must remain constant (no external torques): how can this happen?
For the earth-moon system L = mvr + Iω and so if ω decreases, vr must increase.
How much?
mv²/r = GMm/r², so v = (GM/r)1/2
so
L = mvr = m(GMr)1/2
Hence r must increase: i.e the moon moves away from the earth.
How much?
L = m (GMr)1/2 + Iω
dL/dr = 0 = m (GM/r)1/2 dr/dt + I dω/dt
so
dr/dt = - (rM/G)1/2 R²/m dω/dt
= -2.7 × 1012 × 2.67 × 10-21
= 7.3 × 10-9 ms-1
(i.e. 7 nm/s or 23 cm/yr)
Tidal effects and solid bodies:
e.g. LEP at CERN
It was noticed that the energy of the accelerator was changing on a 12 hour basis (ΔE/E ≈ 10-4)
This corresponds to a change of ΔR ≈ 600 µm (to be compared with 6.5 km for the ring radius.)
Tidal Forces on the Moon:
If the difference between the sides of the moon is larger than the cohesive forces holding it together, it will fall apart.
Small objects are held together by inter-molecular forces: these are very strong, but short-range (i.e. they don't accumulate).
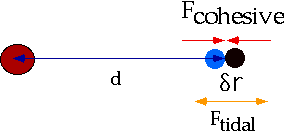
Roches limit: e.g. assume the "moon" is made of two spheres:
Assume the cohesive gravitational force holding one sphere together = the differential gravitational force on that sphere due to the other.
| Hence the minimum distance before the moon breaks up is given by... |
 |
| The cohesive force must exceed the tidal force, so to find when breakup occurs, assume they are equal. |
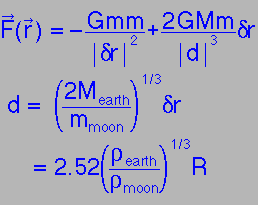 |
Let (δr be the radius of the moon, and R be the radius of the earth, and d is the minimum distance before breakup occurs)
(The numerical constant depends on exactly what assumptions we make for the shape of the moon: obviously ours isn't very sensible.)
Note that the cohesive force is given by internal forces until the moon is about 10 km in radius.
Instability:
| Similar idea: if a satellite moves too far away, then it can be dragged away from the planet. |
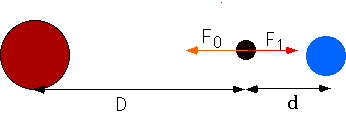 |
We can consider this as a tidal problem again: we need that the tidal force dragging the moon away from the earth > the attractive gravitational force.
| The cohesive force must exceed the tidal force, so to find when breakup occurs, assume they are equal. (D is the earth-sun distance, d is the minimum earth-moon distance before breakup occurs). |
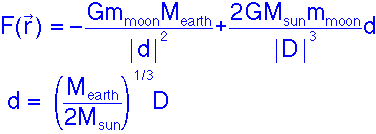 |
What is the maximum distance for the moon?
d = 1.7 × 109 m (≈ 4 × current distance)
When does this happen (assuming, wrongly, that energy loss from the earth remains constant)?
The total distance ≈ 1.2 × 109 m at .23 m/yr
=> 5.2 × 109 yrs (≈ the age of the solar system)
Tidal locking: a (semi-)stable configuration will occur when tidal forces increase the orbital period of the moon and decrease the rotational period until the two are the same. e.g. Earth-Moon, Jupiter-Io
It needn't be locked in 1:1 e.g. Mercury is in 1.5 (rotational) : 1.0 (orbital) lock.
Yet another effect of tides (and frictional forces in general):
Orbits become more circular
Resonances:
Usually attractions of other planets/moons is random and cancels out.
|
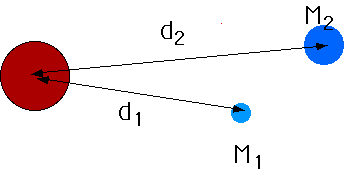 |
However if the period of (e.g) two moons are in a simple ratio, the force will be systematically applied. e.g. if d1/d2 =1.58 P1/P2 = 2, so (assuming M1 is the lighter) it can be kicked out of its orbit.
| We can see this (particularly) in Saturn's rings. Note no material in Cassini's division: This corresponds to a 2:1 resonance with Mimas (innermost large moon of Saturn). |
 |
Precession:
The moon exerts a torque on the bulge of the earth, causing it to precess in the same way as a top The calculation is messy).
|
 |
The sun exerts torque on the earth-moon system, causing the plane of the moon's orbit to precess with a period of 18.6 yrs
|
 |
Relativity:
The executive summary (We'll do it properly using Berry later on)
Special relativity deals with frames of reference which are moving relative to each other. The fundamental assumption is that "The speed of light is the same in all inertial frames", not that "Time is the same in all inertial frames".
The effects are not apparent until velocities become a sizeable fraction of speed of light.
The important results:
| Mass <⇒ Energy (provided that other rules, such as conservation of charge) can be satisfied. |
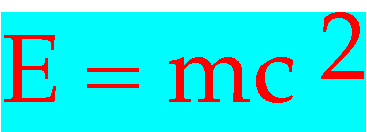 |
Escape velocity:
A particle will escape form the earth if it has positive net energy.
E = 1/2 m v² - GMm/r
br>
so E = 0 ⇒ v²r = 2GM or
v = (2GM/r)1/2
However we can interpret this differently:
What radius would the earth have for a given escape velocity?
R = GM/v²
In particular, if the escape velocity is c,
R = GM/c².
This is the Schwarzchild radius (loosely the black-hole radius) for any mass.
What is this for the earth?
Statutory Warning:
This is a fudge: you cannot treat the photon as a massive particle, nor can you handle a very strong gravitational field as if it were a weak one......
(there are actually two factors of 2 error which cancel out.....weren't we lucky!)
General relativity:
Handles frames which are accelerating w.r.t. each other.
| What is a straight line? |
 |
Why do all masses fall at the same rate?
Pseudo-forces (e.g. centrifugal force)
F = mv²/R = ma, so all bodies undergo the same centrifugal acceleration. All normal forces (e.g. electrical, friction, elastic...) don't produce the same acceleration in all bodies.
Maybe gravity is special
The starting point is the assumption that a massive body curves space around it: hence straight lines are no longer straight.
Geodesic: the shortest time path between 2 points = straight lines in a flat space
Planets are actually moving in straight lines in a curved space...
We can either say:
There is a force called gravity which acts on all energies (and hence attracts photons)
or
There is no such thing as gravity, it's just that masses distort space-time in their neighbourhood.
"lenses extend unwish through curving wherewhon till unwish returns on its unself"
.........................................e.e.cummings
To second order, the gravitational potential is:
V(r) = -GM/r + J²/r² - 2GMJ²/c²r³
What does this look like?
The fact that orbits are closed is a "coincidence", and not true for any potentials except r², 1/r and 1/r²
Hence, we get "rosette" orbits. |
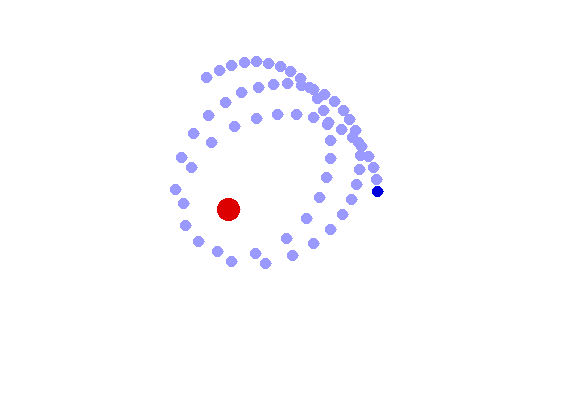 |
It is much less dramatic in practice: the perihelion (closest approach to sun) of Mercury (most dramatic in the solar system) advances by 43" arc/century.
Other consequences of General Relativity: Clocks run slower in gravitational fields:
τ = τ'/(1-2GM/c²r)1/2
in particular, if r = 2GM/c², then τ = 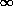
i.e. if I watch a clock at the Schwarschild radius, it appears to have stopped.
An atom is a good clock: frequencies also get shifted.
Hence Gravitational Red Shift:
λ' = λ/(1-2GM/c²r)1/2
where λ is the wavelength that is emitted, and λ' is what I see. |
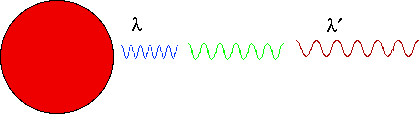 |
A final consequence: gravitational waves
Vibrating charge radiates E.M. waves.
Vibrating mass radiates gravitaty waves.
|
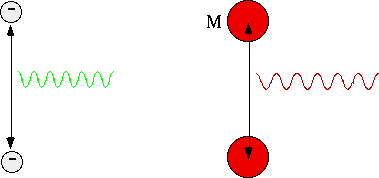 |
Differences: The gravitational force between 2 electrons ≈ 10-42 × electric force .........
Hence (well, more or less hence!) it requires a large amount of mass to produce a gravity wave, and a large amount to see one.
Also, radiation is quadrupole, not dipole, which also means it is still weaker
Hulse and Taylor:
Binary Pulsar PSR1913+16 was discovered in 1974. Like all pulsars, it emits very regular radio pulses every 59 ms. (The frequency is 16.940 539 184 253 Hz: i.e. it is better known than for atomic clocks.)
This consists of two neutron stars, in orbit 106 km in radius, with a period of hours. The change in frequency allows the orbit to be calculated exactly, and can be measured..
The eccentricity = 0.617 130
Periastron (closest approach) precession = 4.22662 0/yr (i.e. 30,000 × that of Mercury)
and that pulsar is losing energy, by gravitational radiation (mass≈1.4 M₀, and accelerations are large).
Hence the 1993 Nobel Prize for this accurate observation which confirms the predictions of General Relativity...
The only part of the solar system we haven't looked at is the Sun
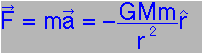
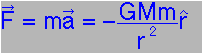
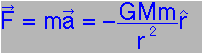
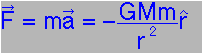
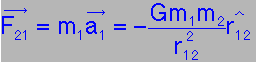 with the changing velocity and acceleration of m1
with the changing velocity and acceleration of m1