Correct answer is
\color{red}{
t_{dyn} = \left( {\frac{1}{{4\pi G\rho }}} \right)^{1/2} \simeq \tau }
Pressure
stops the collapse.
This gives Jeans length and Jeans mass
Jeans length = size of overdense region: anything bigger will collapse
\color{red}{
\lambda _J \approx 2\pi c_s t_{dyn} }
Jeans Mass
Critical mass of matter (not radiation) inside sphere defined by Jeans length
\color{red}{
M_J = \rho _b \left( {\frac{4}{3}\pi \lambda _J ^3 } \right)}
If actual mass M > MJ, sphere will collapse
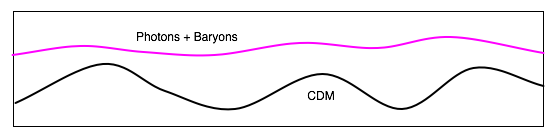
| Before decoupling, matter and radn move together |
 |
| In matter-dom universe cs = b is speed of sound in gas, say few km/s. More accurately
\color{red}{
P = \frac{{\rho kT_m }}{{m_H }} \Rightarrow c_b = \sqrt {\frac{{dP}}{{d\rho }}} = \sqrt {\frac{{kT_m }}{{m_H }}} }
and we found T∼ 3000 K at decoupling. |
 |
Hence before dec.
- \color{red}{
M_J = 4\pi \rho _b \left( {\frac{c}{H}} \right)^3 }
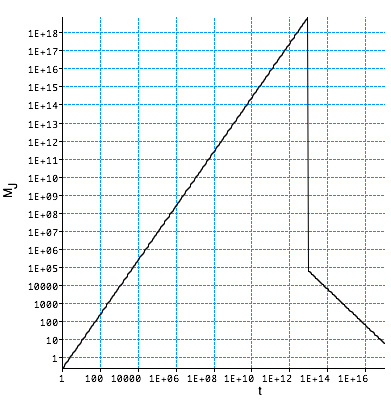
Note ρb ∼ 1/a3 and \color{red}{H\left( t \right) = \frac{{\dot a}}{a} = \frac{1}{{2t}}}
are decreasing,
so MJ is increasing.
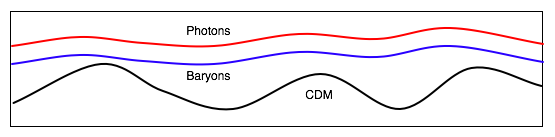
After dec,
\color{red}{M_J \Rightarrow M_J \left( {\frac{{c_B }}{{c_s }}} \right)^3 }
and decreases thereafter
|
 |
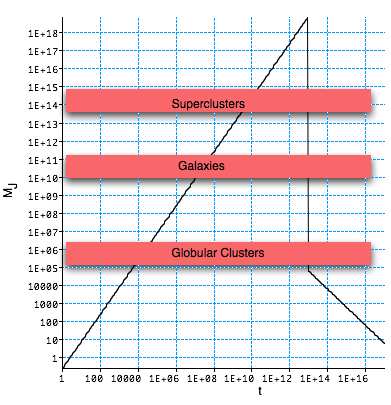
| i.e. we could start collapsing material up to dec, but the lighter structures become unstable and get washed out. After dec, can only create small structs
which gives us a problem |
 |
- Note: ν's don;t help: they freeze out but don't become non-rel: speed of sound ∼ .5 c.
- Interpreted literally, this means that all structures formed in short time around dec.
- but....
Add some WIMPs
These are heavy, freeze out very early and become non-rel.
Repeat previous Jeans analysis, but now include expansion and ignore pressure (since WIMPS are cold!)
as before, consider a sphere, rad R with and over-density δ
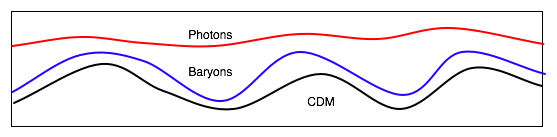
- If we had to wait for matter alone, would only get collapse (growth of fluctuations) after tls or z =1100.
- However, CDM decouples earlier and dominates earlier. Hence Scenario
- CDM decouples
- CDM dominates and clumps
- Baryons decouple
- Baryons clump onto CDM
HDM/CDM
need to be defined:
-
| Hence if HDM consists of (say) 1 eV ν;s which would almost close universe, would have no stable structure smaller than 1017M0, which is too large. |
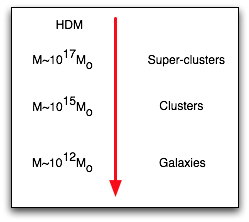 |
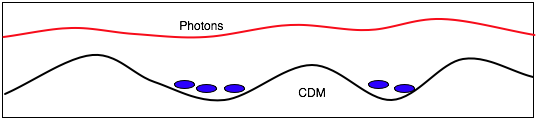
| CDM alows small structures to form immediately, and large structs form from them
|
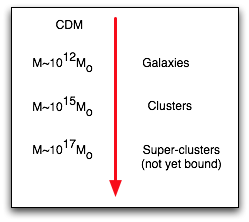
|
| galaxies. {Performed at the National Center for Supercomputer Applications
by Andrey Kravtsov (The University of Chicago) and Anatoly Klypin (New Mexico State University). |
|
Conclusion
We can understand structure formation;
- run simulations,
- compare statistical properties with observations
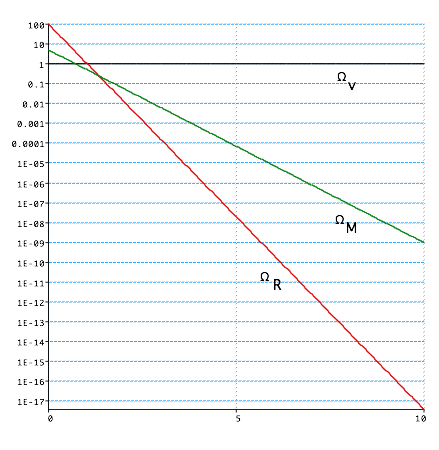
- CDM dominant, but need some HDM mix
- ΩCDM∼ .26
- ΩHDM∼ .03:
- means either ν's have some mass, or have some new unknown HDM component
Inflation
We are left with two major problems: the flatness problem and the horizon problem, and also one you haven't head of: the monopole problem
- Why is the universe large and flat?
- It could naturally be very much smaller, and there is no reason to have Ω=1 (this is the "Why the hell" question!)
- Why is the universe all the same temperature?
- Parts of it have never been in contact. Why does CMBR correlations extend below l = 180?
- As the universe cooled, bits of it spontaneously made phase transitions. This should lead to defects: where are they?
- Huh?
Why the Hell?
At any time, critical energy density is given by
\color{red}{
\varepsilon _c \left( t \right) = \frac{{3c^2 H^2 }}{{8\pi G}}}
so (YAWOWTFE)
\color{red}{
H\left( t \right)^2 = H\left( t \right)^2 \Omega - \frac{{\kappa c^2 }}{{R_0^2 a\left( t \right)^2 }}}
which can be rewritten
\color{red}{
H_0^2 \left( {\Omega _0 - 1} \right) = H\left( t \right)^2 a\left( t \right)^2 \left( {\Omega \left( t \right) - 1} \right)}
so (1-Ω) can never change sign.
| Suppose (for simplicity) we have a radiation-dom. universe (doesn't affect the argument)
\color{red}{
\Omega \left( t \right) = 1 + \left( {1 - \frac{1}{{\Omega _0 }}} \right)a^2 }
- If κ = 0, Ω = 1 for all time
- If κ > 0, then Ω decreases away from 1.
- Ifκ < 0, then Ω increases away from 1.
This is the "flatness problem" |
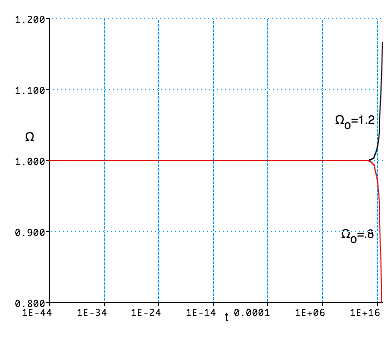 |
| Since we measure Ω now ≈ .1...this means that at the time of the BB, Ω ≈ 1 - 10-60
i.e. Ω = 1 is an unstable critical point |
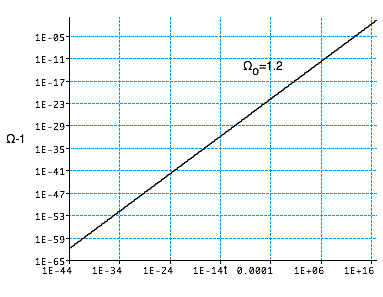 |
The flatness problem is worse than you would think: If the universe started out at 10-44 s with (say) Ω = 3, it would last ≈ 10-35 s (!!!!)
Horizon problem:
Parts of the universe separated by Hubble dist. d > c/H
| More exactly: the most distant object that we can see today is given by the "horizon distance": |
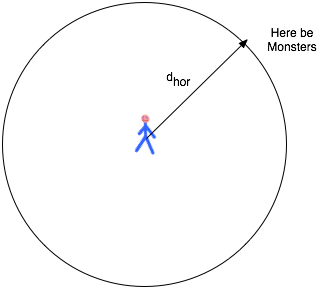
|
in general, this is
\color{red}{
d_{hor} \left( t \right) = ca\left( {t_0 } \right)\int_0^{t_o } {\frac{{dt}}{{a\left( t \right)}}} \Rightarrow c\int_0^{t_o } {\frac{{dt}}{{a\left( t \right)}}} }
| (note light is emitted at t = 0).
If we have a one-component universe, this is
\color{red}{
\frac{{a\left( {t_0 } \right)}}{{a\left( t \right)}} = \left( {\frac{{t_0 }}{e}} \right)^{2/\left( {3 + 3w} \right)} w \ne - 1}
so
\color{red}{
d_{hor} \left( {t_0 } \right) = \frac{c}{{H_0 }}\frac{2}{{1 + 3w}}}
|
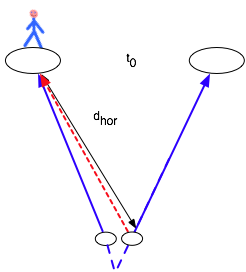 |
so in matter-dom universe (w=0), this is now
\color{red}{
d_{hor} = \frac{{2c}}{{H_0 }} \approx 2.6 \times 10^{26} m}
Note if w <-1/3, dhor=∞: i.e. can see all the universe.
The inflationary universe
solves these problems:
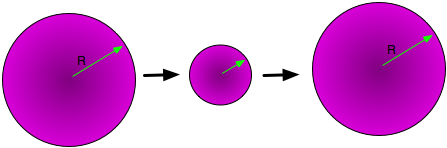
| consider a very small volume of the (original) universe.
e.g. at t = 10-34 s, the size of the horizon is d = ct = 10-23 cm (≈ 10-8 size of a proton)
The inflationary phase leads to an increase in the size of universe by 1080. |
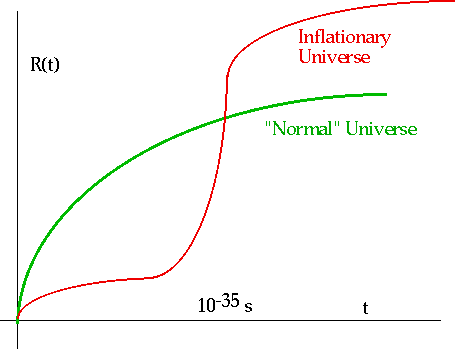 (diagram not exactly to scale!) (diagram not exactly to scale!) |
| An inflationary phase "smoothes out the wrinkles". The temperature in this volume was already in equilibrium. Now, after inflation, it is much larger and smoother than before. |
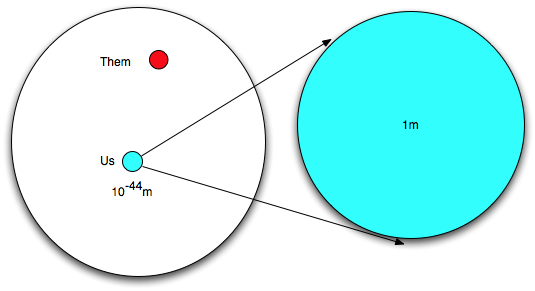 |
How do we get this? This was one "special case": if vacuum itself has an energy ρv=Λ/3 ≠0? Obviously
$$
\color{red}{
\frac{{d\rho _v }}{{dt}} = 0}
$$
so (setting ρm= ρr=0 for simplicity) we can use $$
\color{red}{
\left( {\frac{{\dot a}}{a}} \right)^2 = \frac{\Lambda }{3}}
$$
which is our previous results with w = -1: this gives$$
\color{red}{
a(t) = a_0 e^{\sqrt {\frac{\Lambda }{3}} t} }
$$
Note that
\color{red}{
H_i = \frac{{\dot a}}{a} = \sqrt {\frac{{\Lambda _i }}{3}} }
i.e. Hubble param is constant.
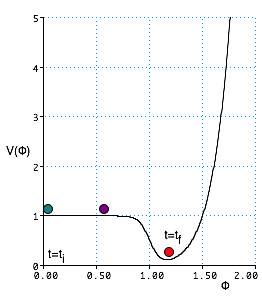
Assume that inflation switches on at ti and off at tf. Then scale param at start of inflation is ai so before
\color{red}{
a\left( t \right) = a_i \left( {\frac{t}{{t_i }}} \right)^{1/2} }
so
\color{red}{
H_i = \frac{{\dot a}}{a} = \frac{1}{{2t_i }} \approx 10^{36} s^{ - 1} }
(which obviously fixes Λ)
Usual to talk about E-foldings:
\color{red}{
N = \frac{{t_f - t_i }}{{H_i }}}
Number of times that universe expanded by a factor of e.
Flatness problem
At 10-36 s, the universe could have deviated from Ω = 1.
\color{red}{
\Omega \left( t \right) - 1 = \frac{{\Omega _i - 1}}{{a\left( t \right)^2 }}}

After inflation, the density hasn't changed (remember steady state model?) but the universe is 1043 times larger!
This means that it can never deviate much from Ω = 1: i.e. flatness problem is fixed.
Horizon problem
\color{red}{
d_{hor} \left( t \right) = ca\left( {t_0 } \right)\int_0^{t_o } {\frac{{dt}}{{a\left( t \right)}}} \Rightarrow c\int_0^{t_o } {\frac{{dt}}{{a\left( t \right)}}} }
Before inflation,
\color{red}{
d_{hor} = \frac{{2c}}{H} = 2ct_i \sim 10^{ - 29} m}
(seriously: about 10-14x size of proton!)
after inflation
\color{red}{
d_{hor} \left( {t_f } \right) = e^N c\left( {2t_i + \frac{1}{{H_i }}} \right) \sim 3ct_i e^N \sim 1 pc}
What we really want to do is to ensure that the currently visible universe was small enough prior to inflation that it could be in thermal contact.
Surface of last scattering is at zls ≈1100 so proper distance
\color{red}{
\begin{array}{l}
d_p \left( {t_0 } \right) = c\int_{t_e }^{t_o } {\frac{{dt}}{{a\left( t \right)}}} = c\int_{t_e }^{t_o } {\frac{{dt}}{{\left( {\frac{t}{{t_0 }}} \right)^{2/3} }}} = \frac{{3c}}{{t_0 }}\left( {1 - \left( {\frac{{t_e }}{{t_0 }}} \right)^{1/3} } \right) \\
= \frac{{2c}}{{H_0 }}\left( {1 - \frac{1}{{\sqrt {1 + z} }}} \right) \approx 4 \times 10^{26} m = 1.4 \times 10^4 Mpc \\
\end{array}}
(universe is matter-dom since then, so we know \color{red}{a\left( t \right) = \left( {\frac{t}{{t_0 }}} \right)^{2/3} }
| After inflation ended,
\color{red}{
d_p \left( {t_f } \right) = a_f d_p \left( {t_0 } \right) \approx 1m}
Before inflation started,
\color{red}{
d_p \left( {t_i } \right) = e^{ - N} d_p \left( {t_f } \right) \approx 10^{ - 44} m}
which is much smaller than horizon |
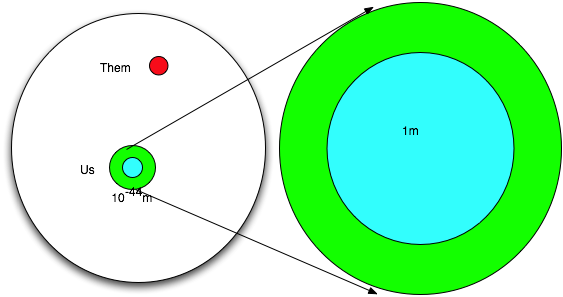 |
Monopole problem
Effectively, monopoles become so dilute at most one in our observable universe (but Cabrera saw it!)
Origins of Inflation: preamble
- Need to turn on inflation at ti
- Turn it off at tf
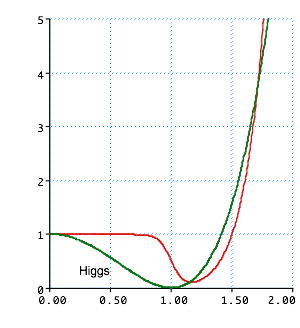
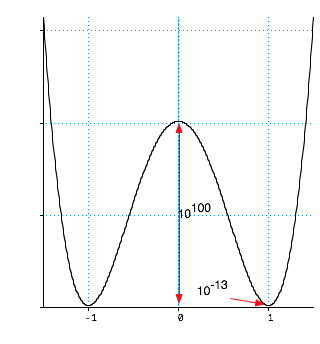
Need a scalar field (inflaton) with large energy density:
- e.g. ES field E has \color{red}{V\left( E \right) = \frac{1}{{2\varepsilon _0 }}E^2 }
- However time varying fields add a KE term.
- For a single particle in (e.g.) SHO\color{red}{H = \frac{1}{{2m}}p^2 + \frac{1}{2}m\omega ^2 x^2 }
(H is Hamiltonian, not Hubble param!).
\color{red}{
\varepsilon _\varphi = \frac{1}{2}\rho \left( {\frac{{\partial \phi }}{{\partial t}}} \right)^2 + \frac{1}{2}\rho c^2 \left( {\frac{{\partial \phi }}{{\partial x}}} \right)^2 }


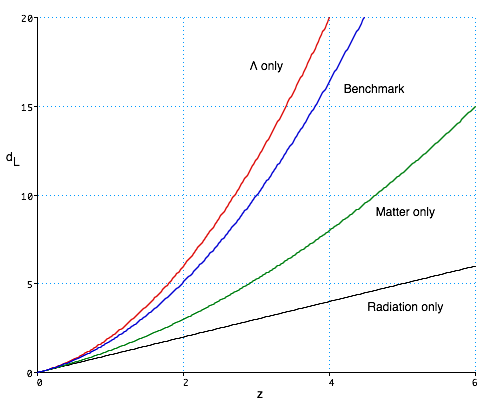
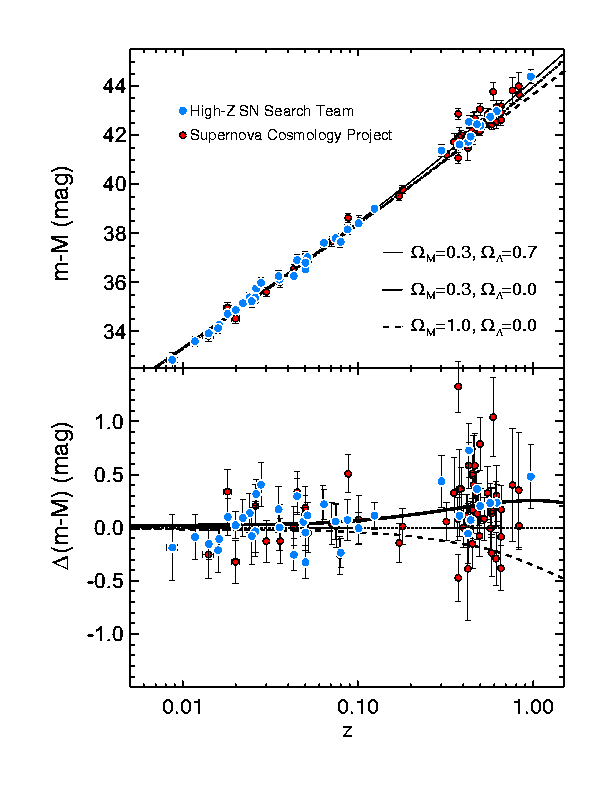
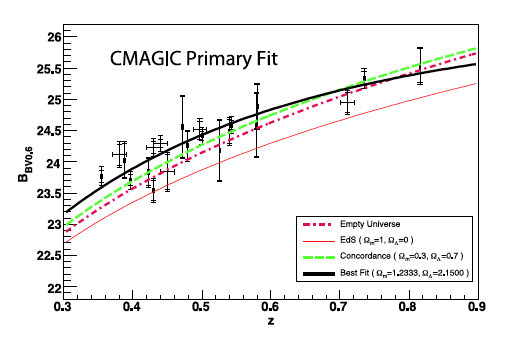
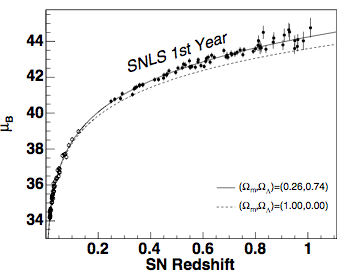
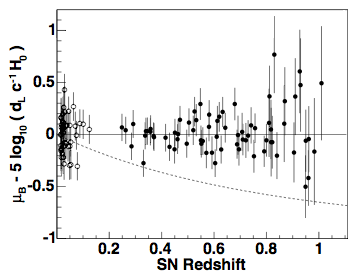
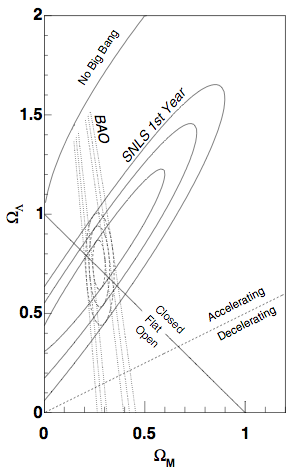
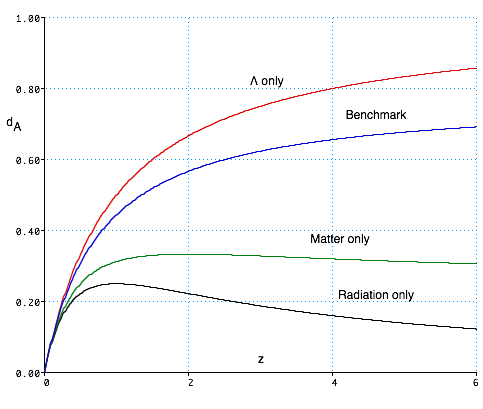
















 (diagram not exactly to scale!)
(diagram not exactly to scale!)