Now the details............
Stars: General Equations
At every point in star, there are six quantities (which depend on time as well) . Stellar structure problem is to relate them
- Pressure P(r)
- Density ρ(r)
- Temperature T(r)
- Luminosity L(r)
- Mass "inside" m(r)
- Energy Production ε(r)
|
 |
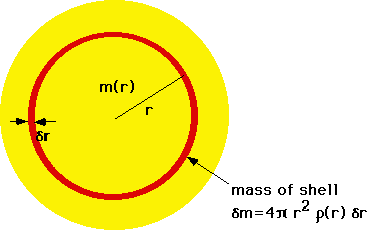
Mass-density is easy
\color{red}{
\delta m = 4\pi r^2 \rho \left( r \right)\delta r}
so
\color{red}{
\frac{{dm}}{{dr}} = 4\pi r^2 \rho \left( r \right)}
Note earlier calc was a special case ρ = constant |
 |
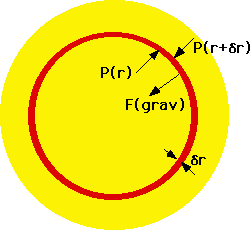
| Hydrostatic equilibrium: Shell must be stable, so forces must balance, Grav. force on shell \color{red}{\begin{array}{l}
F_G = - \frac{{Gm(r)M_{shell} }}{{r^2 }} \\
= - \frac{{Gm(r)4\pi r^2 \rho \left( r \right)\delta r}}{{r^2 }} \\
\end{array}}
Pressure must balance this.
\color{red}{
\delta P = P\left( {r + \delta r} \right) - P\left( r \right)}
(must be negative)
Total force due to pressure
\color{red}{
F_P = 4\pi r^2 \delta P = - F_G }
Hence
\color{red}{
\delta P = - \frac{{Gm\left( r \right)\rho \left( r \right)\delta r}}{{r^2 }} \Rightarrow \frac{{dP}}{{dr}} = - \frac{{Gm\left( r \right)\rho \left( r \right)}}{{r^2 }}}
(- sign means pressure decreases as we move outwards) |
 |
e.g. assuming density is constant, what is central temp and pressure of sun?
Where does the pressure come from?
Equation of state relates pressure to temp and density. Three possible ways:
- Gas Pressure
- Radiation pressure
- Degeneracy pressure
- Gas pressure:
\color{red}{
PV = NRT}
or (more useful for us)
\color{red}{
P = \frac{{k\rho T}}{{\mu m_H }}}
All three occur in all stars, but
- Gas Pressure important in "normal" stars (M < 2M₀)
- Radiation pressure important in hot (i.e. massive) stars
- Degeneracy pressure totally unimportant at normal densities: need ρ ∼ 109 kg.m-3 i.e. white dwarfs (will return to this later)
Energy transport: i.e. how does energy move out from solar core?
- Conduction: totally unimportant for any star, since pressures are low
- Radiation
- Convection
Radiation: Temp difference across shell is δT
Hence the energy/unit area radiated out
\color{red}{
F\left( r \right) = \sigma T\left( r \right)^4 }
Energy radiated inwards:
\color{red}{
F\left( {r + \delta r} \right) = \sigma T\left( {r + \delta r} \right)^4 }
So the difference is
\color{red}{
\delta F = 4\sigma T\left( r \right)^3 \delta T}
|
 |
This energy must be absorbed by the layer: amount absorbed δF
- ∝ amount of radiation
- ∝ amount of material
- ∝ thickness of layer
- ∝ "lack of transparentness" = opacity κ(r,λ)
- (e.g. glass would have opacity 0 for optical γ's)
\color{red}{
\delta F = - \kappa \left( r \right)\rho \left( r \right)F\left( r \right)\delta r}
- Combine and use Luminosity = total outwards flux
\color{red}{
L\left( r \right) = 4\pi r^2 F\left( r \right)}
gives
\color{red}{
\frac{{dT}}{{dr}} = - \frac{{\kappa \left( r \right)\rho \left( r \right)L\left( r \right)}}{{16\pi r^2 \sigma T\left( r \right)^3 }}}
-
(actually we cheated slightly: the correct equation multiplies this by 4/3, due to an angular averaging).
- Note dT/dr is negative: the luminosity increases
How do we calculate κ(r,λ,T)?
Extremely difficult from first principles Only people who really care are bomb makers: hence only good codes are at Los Alamos and Livermore (and no, you can't borrow them!!)
A reasonable approx. that works for ionised gases over a large range is
\color{red}{
\kappa = C\frac{{Z\left( {1 + X} \right)\rho }}{{T^{7/2} }}}
(i.e. it doesn't depend on wavelength)
Convection
Much harder: if the opacity is very high, the gas will just heat up at the bottom, which will make it less dense than cooler gas above
Imagine a bubble of gas which is slightly less dense than its surroundings: if it rises and the density decreases faster than the surrounding gas, it will continue to rise.
Adiabatic temp gradient.
\color{red}{
P_1 V^\gamma _1 = P_2 V^\gamma _2 }
and
\color{red}{
P_1 ^{\frac{1}{\gamma } - 1} T^{} _1 = P_2 ^{\frac{1}{\gamma } - 1} T^{} _2 }
Hence:
\color{red}{
T^{} = CP_{} ^{1 - \frac{1}{\gamma }} }
so
\color{red}{
\frac{{dT}}{{dr}} = C\left( {1 - \frac{1}{\gamma }} \right)\frac{1}{{P_{} ^{\frac{1}{\gamma }} }}\frac{{dP}}{{dR}} = C\left( {1 - \frac{1}{\gamma }} \right)\frac{T}{P}\frac{{dP}}{{dR}}}
If the actual temp gradient in a star is greater than this, then convection will set in. Unfortunately, it doesn't tell you how much energy is moved around!
|
 |
- Note same happens on earth on hot summer days: air heated near ground is adiabatically unstable, and rises => thunderstorms
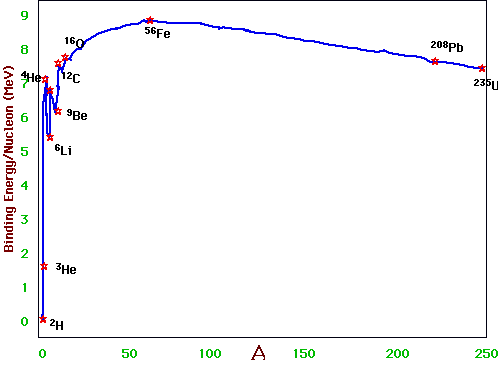
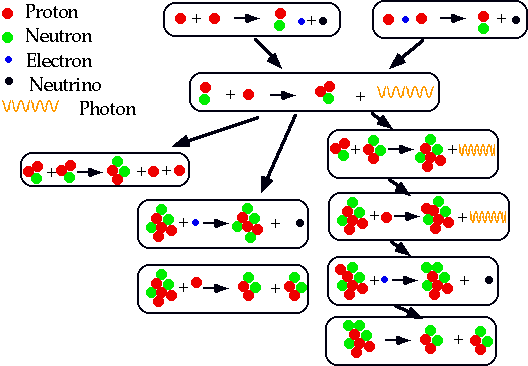
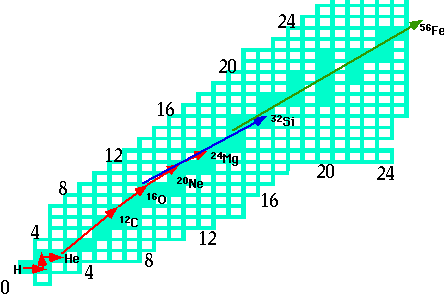
Finally energy generation: obviously(?)
\color{red}{
\frac{{dL}}{{dr}} = 4\pi r^2 \rho \left( r \right)\varepsilon \left( {r,T} \right)}
ε(r,T) is energy generated/unit mass:
it will depend on T:
for H cycle (PP cycle) ε ∝ T⁴
Equations In summary
- Mass-density
\color{red}{
\frac{{dm}}{{dr}} = 4\pi r^2 \rho \left( r \right)}
�
�
- Eqn. of State:
\color{red}{
P = \frac{{k\rho T}}{{\mu m_H }}}
�
�
- Luminosity/Energy generation
\color{red}{
\frac{{dL}}{{dr}} = 4\pi r^2 \rho \left( r \right)\varepsilon \left( r \right)}
�
- Energy transport
\color{red}{
\frac{{dT}}{{dr}} = - \frac{{3\kappa \left( r \right)\rho \left( r \right)L\left( r \right)}}{{64\pi \sigma r^2 T^3 }}}
- Hydrostatic Equilibrium
\color{red}{
\frac{{dP}}{{dr}} = - \frac{{Gm(r)\rho \left( r \right)}}{{r^2 }}}
�
- Opacity:
\color{red}{
\kappa \left( r \right) = \frac{{CZ\left( {1 + X} \right)\rho \left( r \right)}}{{T^{7/2} }}}
�
- Energy generation: (roughly for hydrogen burning)
\color{red}{
\varepsilon \left( r \right) = a\left( {\frac{T}{{T_0 }}} \right)^4 }
- Note that stars are much simpler than (e.g..) human beings: on the other hand we still need a computer to solve for one!
�
A very simplified model which can be solved by hand (or preferably by computer algebra!)
| Guess
\color{red}{
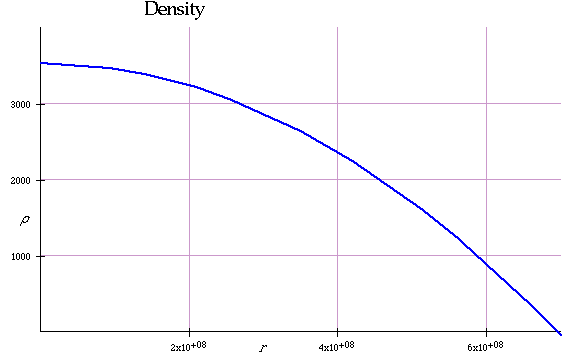
\rho \left( r \right) = \rho _0 \left( {1 - \frac{r}{R}} \right)^2 }
This vanishes at the surface of the sun (as it must). Then
\color{red}{
m\left( r \right) = \int_0^r {4\pi r'^2 } \rho \left( {r'} \right)dr'}
can be found exactly and m(R₀) = M₀
⇒
\color{red}{
\rho _0 = \frac{{15M_0 }}{{8\pi R^3 }} \sim 3500}
(too low) |
 |
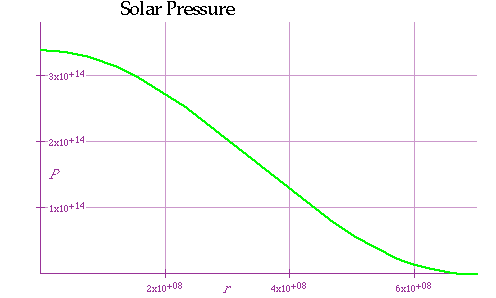
| Then<
\color{red}{
P\left( r \right) = \int_0^r G \frac{{\rho \left( {r'} \right)m\left( {r'} \right)}}{{r'^2 }}dr' + P_0 }
(what is P(Ro?)
gives
\color{red}{
P_0 = \frac{{15GM_0^2 }}{{16\pi R_0^4 }}}
|
 |
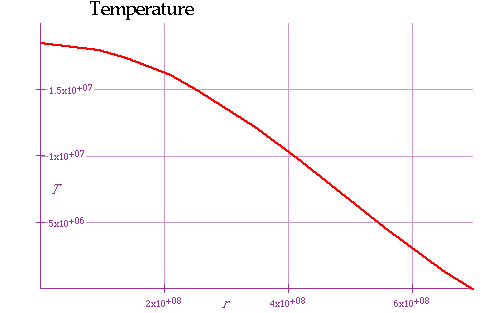
| Then
\color{red}{
P = \frac{{k\rho T}}{{\mu m_H }}}
gives
\color{red}{
T_0 = \frac{{\mu m_H GM_0 }}{{2kR_0}} \sim 7.2 \times 10^6 K}
(best estimate is 14x106K, so it's a bit low |
 |
| One can get the luminosity from this (assuming H cycle) |
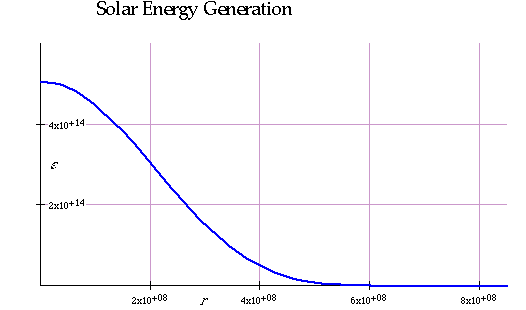 |
-
| and fit the result to the total luminosity of the sun |
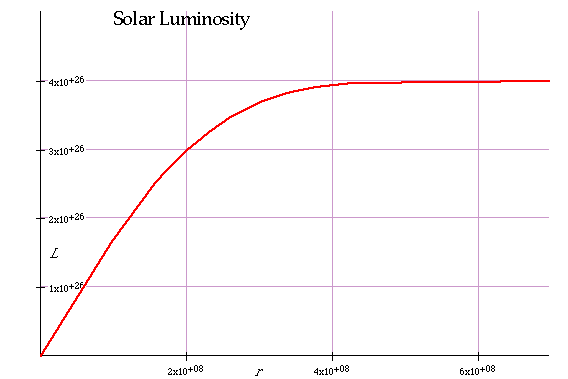 |
Quantitatively this star is not dense enough at the origin, so pressure and temp are too low, so core is too big.T
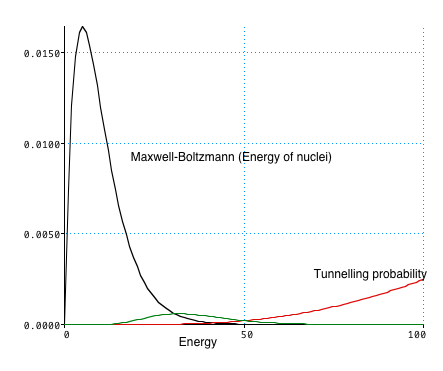
Nuclear reactions: long preamble
requires a knowledge of the forces and particles involved, conservation laws and reaction rates.
Forces
| Strong force is the force that binds together nucleons to make nuclei, weak force is force that causes β-decay. Believe there are only 4 forces in nature |
 |
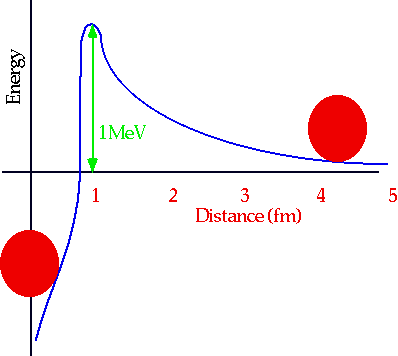
Range: if it is ∞ then F ∝ 1/r², else it cuts off at distance shown
Strength: roughly the relative strength of the forces at a distance of 1 fm.
Although (e.g.) strong force>>>E.M at 1 fm (=10-15 m), it vanishes totally beyond 10-14 m. E.M >>> Gravity, but it tends to cancel out since most matter is electrically neutral, whereas mass accumulates.
The weaker the force, the more particles feel it!
Particles
: of the 450 (or so) elementary particles, only 5 are important to astrophysics
| Strength also gives us (very roughly) the depth that a particle will penetrate matter without interacting:
e.g. a proton will penetrate a few mm, a X-ray photon a few cm, a neutrino several parsecs! |
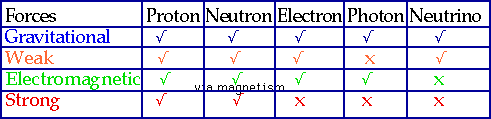 |
Antiparticles:
For every particle, with given quantum numbers, there is a corresponding anti-particle with the properties flipped:
e.g. electron has charge -1.6x10-19 Coulomb.
Positron has same mass, charge = 1.6x10-19 C
Conservation laws
- Mass-energy conservation:
- Usually easier to quote elementary particle masses in terms of energy, measured in eV.
- e.g. "mass" of electron \color{red}{m_e c^2 = 511keV}
�
- Conservation of momentum:
- Usually (from point of view of astrophysics) means that reactions are:
2 bodies ⇒ 2 bodies
- e.g. \color{red}{p + n \to d + \gamma }
� is allowed
-
\color{red}{p + n \to d}
� (where the d moves off with the extra energy) is forbidden.
Conserved Quantum Numbers
- Conservation of charge
\color{red}{
n \to e^ - + \gamma }
� is forbidden: Algebraic sum of charges at end of reaction must = sum at start
note
\color{red}{
\gamma \to e^ + + e^ - }
� is allowed
- Conservation of baryon number:
The process
\color{red}{
p \to e^ + + \gamma }
� is not forbidden by anything: however experimentally it does not occur:
No of (protons + neutrons) is always the same in a reaction:
Easiest to say that p & n carry baryon number B = 1, rest carry 0
- Conservation of lepton number: Number of (electrons + neutrinos) is conserved
L is lepton number = 1 for electrons,
-1 for positrons
(\color{red}{{\bar \nu }}
� means anti-neutrino: what is an anti-neutrino? one with L = -1).