BIT1002 Waves and Sound
Simple Waves
Easiest to visualize are water waves or waves in string
One dimensional waves: e.g.
- Waves in slinky
- Waves in string
- Sound waves
- Light Waves
- Usually medium is left undisturbed by passage of wave (can't tell if a water wave has been past). Waves can be
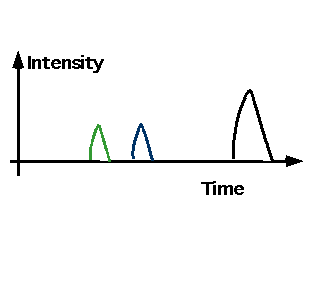
- Pulses
- Continuous Waves
- Standing Waves
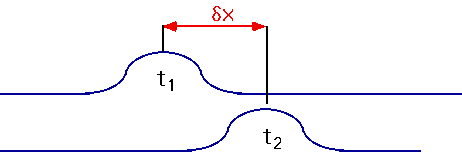
Pulses
If wave travels a distance
δx in δt = t₂-t₁
then
v = δx/δt
|
 |
Continuous waves
| Need not be periodic |
|
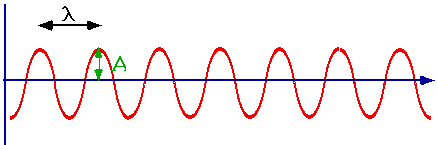
Periodic Waves
Continuous waves which repeat are periodic waves
| Because it is mathematically simple, we will often use harmonic waves: i.e. sine waves:
As before v is speed at which one crest (or trough) moves
|
|
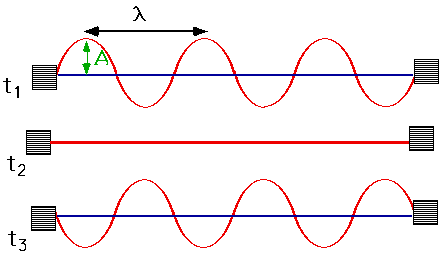
Standing waves
| e.g. vibrating violin string. |
|
Waves can be
- Longitudinal
- Transverse
Longitudinal Waves
Waves can be
- Longitudinal
- Transversei.e. particles move perpendicular to wave
- Longitudinal: i.e. particles move in direction of wave
| e.g. Slinky |

|
- Sound Waves
| Molecules move backwards and forwards to create regions of higher or lower density. Note sound travels through a solid in exactly the same way |
 |
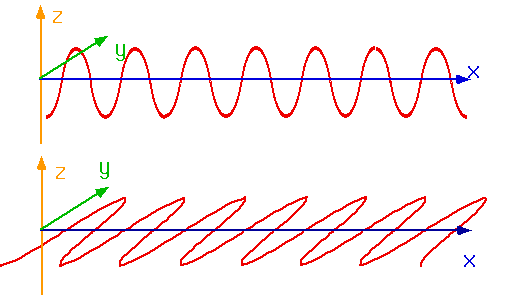
Transverse waves
where the movement is perpendicular to the velocity
- e.g. String, light, water-waves.....
- or slinky!!
-
| Tranverse waves can be polarized in the vertical plane, or the horizontal plane or anywhere in between |
|
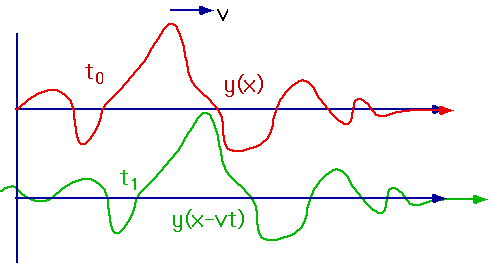
Wave Function
| The wave function describes the shape of the wave: if the wave is non-dispersive (i.e. doesn't change shape)
y(x-vt) describes the shape at any time t |
 |
- Because it is mathematically simple, we will often use sine waves: Harmonic waves
y(x,t) = A sin(2πx/λ-vt)
- Obviously
-
Speed = wavelength x frequency
-
v = λf
- (why?)
A travelling wave:
What is correct description of this wave?
- What is λ?
- What is the velocity of the wave v?
- What is f?
- What is A?
|
t = 0.0s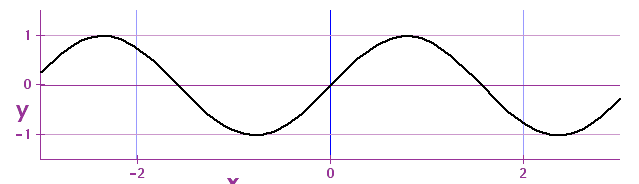
t = 0.1s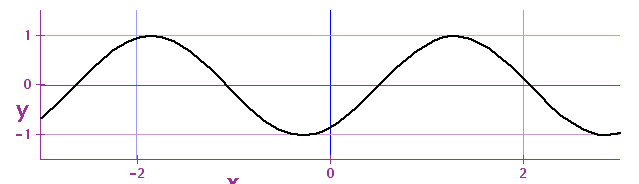
t = 0.2s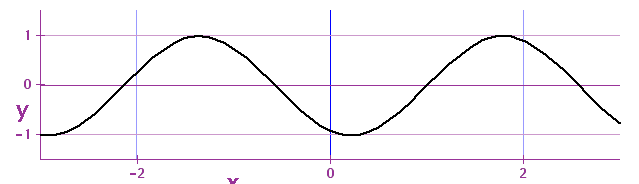
|
Speed of Waves
What governs the speed of a wave?
Sound is often produced by strings: speed of wave probably depends on
- mass of string [mass] = M, length [length] = L, tension [tension] = [Force] = MLT-2
- and we want [v] = LT-1
- only possibility is
v = C(TL/M) 1/2
but M = (volume) x (density)= AL ρ so
v= C(T/ρA) 1/2
where ρ is density and A is area and C is a number . In this case, C = 1 (we got lucky!), |
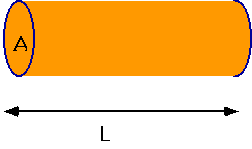 |
- so
v = (T/ρA) 1/2
- Why is this plausible?
Interference
| Waves will pass through each other with no (permanent) effect on each other.
Total displacement will consist of sum of individual displacements e.g. collision of two pulses |
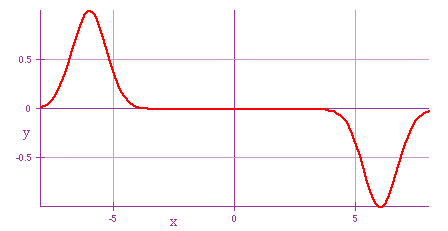
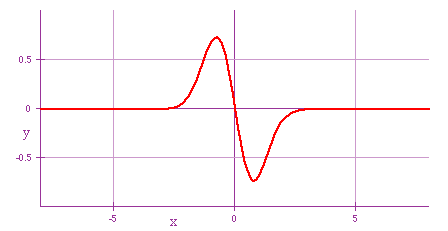
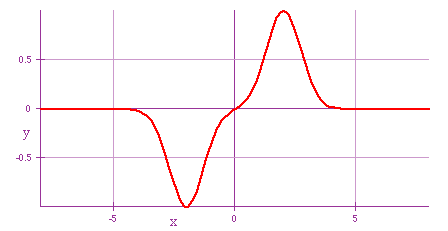
|
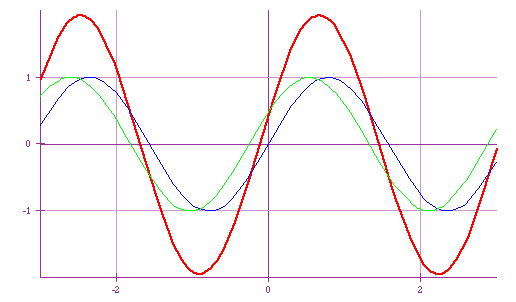
Harmonic Waves
| We are usually more concerned about interference between harmonic waves
See how two sin waves add |
 |
Formally this is done by adding two sine waves
\color{red}{
\begin{array}{l}
y_1 \left( x \right) = A\sin \left( {kx} \right) \\
y_2 \left( x \right) = A\sin \left( {kx + \delta } \right) \\
\end{array}}
so
\color{red}{
\begin{array}{l}
y\left( x \right) = y_2 \left( x \right) + y_1 \left( x \right) \\
= A\left[ {\sin \left( {kx} \right) + \sin \left( {kx + \delta } \right)} \right] \\
\end{array}}
giving
\color{red}{
y\left( x \right) = 2A\cos \left( {\frac{\delta }{2}} \right)\sin \left( {kx + \frac{\delta }{2}} \right)}
- What happens to the waves if δ =0
- What happens to the waves if δ =π
- What happens to the waves if δ =2π
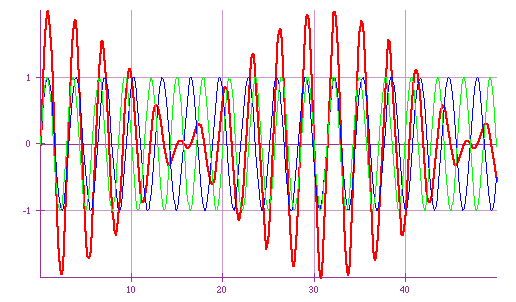
What if the frequencies of the waves are not exactly the same?
-
| If k₁ and k₂ are different, then they will add up constructively at times and destructively at others. The result is a wave that is sometimes large and sometimes vanishes. See the animation. |
 |
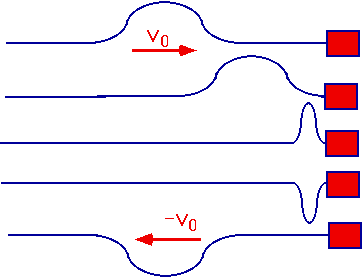
Reflection of waves
Initially in 1-D: can see reflection and refraction.
Easiest to see with a pulse.
Wave exerts upward force on support
=> downward force on rope
=> inversion of original wave |
 |
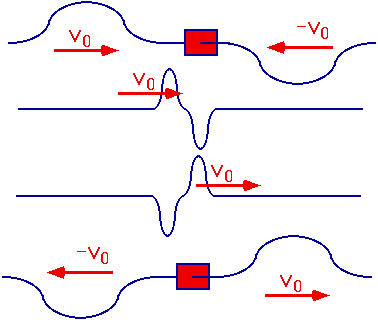
| Can also be thought of as superposition of two pulses travelling in opposite direction |
 |
|
- If end is free to move wave is not inverted
- No force on free end
- So wave is just reflected
|
 |
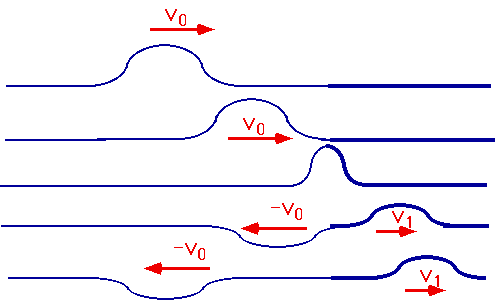
Reflection from an "interface": Wave is partially reflected and partially transmitted
Try the animation
-
| Note: "refracted" wave propagates at a different speed. |
 |
-
| What happens when a light wave hits glass?
Some is always reflected |

|
- Similar effect if we go from dense to less dens medium (glass to air)
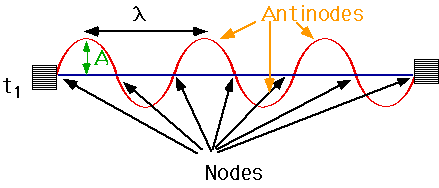
Standing waves
Waves which do not travel (!)
Try the animation
- Simplest is a guitar string
- Ends don't move: can only fit a fixed number of half-waves into the string
- L = (n/2) λ, n = 1,2,3,4,
- These are known as "harmonics": n=1 is fundamental, n = 2 is "first harmonic" and so on.
|
 |
-
| Nodes are points were string does not move: points half way between with maximum motion are antinodes. |
 |
Sound
Practically: we are very interested in sound, since it forms such a large part of our communication.
| Most sound waves are set up by standing waves e.g. guitar has all wavelengths that satisfy (n/2)λ = L so frequencies are
f0 = 1/2v/L fundamental
f1 = 2/2v/L 1st harmonic
fM = M/2 v/L (M-1)th harmonic
In principle, all of these can be excited, but in practice the amount of energy required for higher harmonics is larger, so that they are less easily excited.Hence actual note heard is superposition of many frequencies
|
 |
e.g. a violin string has an area of 10-6 m2, a density of 3000 kg m-3 and a tension of 200 N.
- What would be the speed of a wave in it?
- What notes would it produce if it has a length of 40 cm?
- In terms of this physics, why does
- Increasing/decreasing the tension increase/decrease the pitch?
- Thicker strings play lower notes?
Notes and Music
- Historically, we have notes described in terms of octave:
C
Db
D
Eb
E
F
Gb
G
Ab
A
Bb
B
- One octave = doubling of frequency
| C | 8.2 | 16.4 | 32.7 | 65.4 | 130.8 | 261.6 | 523.3 | 1046.5 | 2093.0 | 4186.0 | 8372.0 |
| Db | 8.7 | 17.3 | 34.6 | 69.3 | 138.6 | 277.2 | 554.4 | 1108.7 | 2217.5 | 4434.9 | 8869.8 |
| D | 9.2 | 18.4 | 36.7 | 73.4 | 146.8 | 293.7 | 587.3 | 1174.7 | 2349.3 | 4698.6 | 9397.3 |
| Eb | 9.7 | 19.4 | 38.9 | 77.8 | 155.6 | 311.1 | 622.3 | 1244.5 | 2489.0 | 4978.0 | 9956.1 |
| E | 10.3 | 20.6 | 41.2 | 82.4 | 164.8 | 329.6 | 659.3 | 1318.5 | 2637.0 | 5274.0 | 10548.1 |
| F | 10.9 | 21.8 | 43.7 | 87.3 | 174.6 | 349.2 | 698.5 | 1396.9 | 2793.8 | 5587.7 | 11175.3 |
| Gb | 11.6 | 23.1 | 46.2 | 92.5 | 185.0 | 370.0 | 740.0 | 1480.0 | 2960.0 | 5919.9 | 11839.8 |
| G | 12.2 | 24.5 | 49.0 | 98.0 | 196.0 | 392.0 | 784.0 | 1568.0 | 3136.0 | 6271.9 | 12543.9 |
| Ab | 13.0 | 26.0 | 51.9 | 103.8 | 207.7 | 415.3 | 830.6 | 1661.2 | 3322.4 | 6644.9 | 13289.8 |
| A | 13.8 | 27.5 | 55.0 | 110.0 | 220.0 | 440.0 | 880.0 | 1760.0 | 3520.0 | 7040.0 | 14080.0 |
| Bb | 14.6 | 29.1 | 58.3 | 116.5 | 233.1 | 466.2 | 932.3 | 1864.7 | 3729.3 | 7458.6 | 14917.2 |
| B | 15.4 | 30.9 | 61.7 | 123.5 | 246.9 | 493.9 | 987.8 | 1975.5 | 3951.1 | 7902.1 | 15804.3 |
Nano-guitar.
| To produce waves of 1m wavelength need instrumentent about 1m in size . If we have a much smaller intrument we produce much higher frequencies
e.g. nanoguitar. 10 μ long, trings are ∼ 50nm in diameter, played with laser beam. |
 © Craighead research group, Cornell University
|
-
Notes and Music
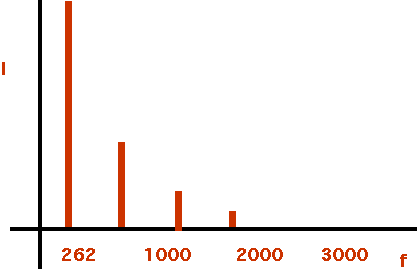
| Why does same fundamental on different instruments sound different?: Violin (bowed) |
 |
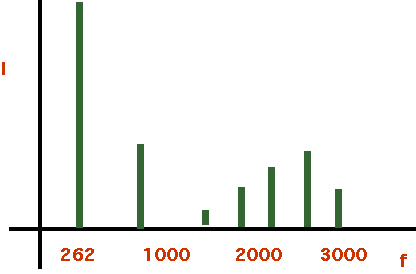
| Clarinet |
 |
Wind Instruments
| Most wind instruments have one open end e.g. flute, oboe, beer-bottle, organ... |

|
Watch the animation
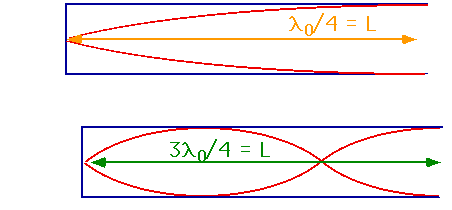
Note what is really happening is that the molecules move a lot at the antinodes but are stationary at the nodes.In particular,there is no motion at the closed end. The fundamental in this case has 1/4 wave
λ = 4 L
λ = 4L/3
This is 3/4 wave.
|
|
- in general .
λ = 4 L/(2n+1)
-
Hence frequency
f = (2n+1) v/(4L)
Note harmonics are not one octave higher.
- e.g. A beer bottle is about 25 cm high. What would you expect the fundamental note to be at? (speed of sound = 330 ms-1)
A beer bottle is about 25 cm high. What would you expect the fundamental note to be at? (speed of sound = 330 ms-1)
- 33 Hz
- 330 Hz
- 3.3 kHz
- 33 kHz
In general, each frequency will have a different amplitude, and the sound depends on this.
Energy in waves:
| Note how the string moves: Not only does the wave move forward, but each individual particle is displaced. This means a wave carries energy. Each particle would have
P.E. = 1/2 k x ²
where x is the maximum displacement. Also
K.E. = 1/2 m v ² so more rapidly oscillating string means larger velocity so... |

|
- power in wave ∝ square of amp.
∝square of frequency
-
P∝ ω ²|A|²
- i.e. double the amplitude, 4 times the energy:
- this means it is harder to excite large amplitudes and high frequencies.
- generally true for any kind of wave.
- Note the particles need not just move up and down: In a water wave, they move in a circle
Energy in sound waves:
We are sensitive to power/unit area: this is intensity I
\color{red}{
I = \frac{{\delta P^2 }}{{2\rho c}}}
- δP = change in pressure ~amplitude of wave
- ρ = density of air
- c = velocity
Units of I? watts/m2: check
[δP] = Force/area = MLT-2/L2 = ML-1T-2,
[ρ]= ML-3,
[c] = LT-1
[I] = (ML-1T-2)2/( ML-3 LT-1) = M T-3
-
[watts/m2] = [energy/(time*area)] =
ML2T-2/(TL2) = ML2T-3/L2 = M T-3
e.g. maximum overpressure the ear can stand is ~ 30 Pa (atmos pressure ~105 P)
- What fraction is this?
- What is the power absorbed by the ear at maximum allowable level?
- We usually express this in logarithmic form (What we hear is log(I), not I)
-
β = 10 log(I/I0)
- where I0 is the faintest sound we can hear (threshold of hearing ~10-12 watts/m2).
- Note this corresponds to an amplitude given by
I = 1/2 ρωv 2A2
- This implies an amplitude of ~10-11, (for f ~ 1kHz) which is less than size of an atom!
β is loudness in decibels
- whisper β ~ 50 db
- conversation β ~ 70 db
- pain threshold β ~ 120 db
- Dire Straits β~ 130 db
e.g. my amplifier puts out 100 W. How much louder does it sound at 100 W than it did at 20?
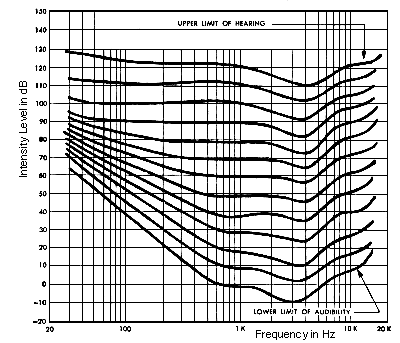
| Note that our hearing response is not uniform at all frequencies: Top curve is threshold of pain, bottom is threshold of hearing
|
 . . |
- You can try this out for yourself at the University of New South Wales site
We also use db to express the signal to noise ratio:
- all sound reproduction devices have hiss or other sounds.
- e.g. CD players have s-n ratios of ~80 db.
- What is the ratio of the intensities of the signal and noise
Doppler Effect
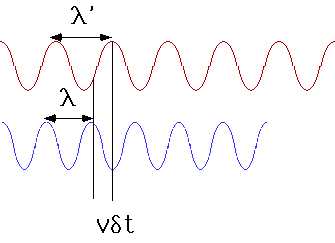
Waves coming from a moving source have their frequency and wavelength changed. Watch the animation.
- During the time taken to emit one wavelength, the emitter moves away a distance v ΔT, i.e. \color{red}{\lambda ' = \lambda + v\delta t}
- Time taken to emit one λ is \color{red}{
\delta t = \frac{\lambda }{c}
}.
- Hence $$
\color{red}{
\lambda ' = \lambda \left( {1 + \frac{v}{c}} \right),f ' = \frac{f}{{\left( {1 + \frac{v}{c}} \right)}}}
$$
|
 |
- This is red-shift: v >0, λ' > λ and f' < f.
- If the object is moving towards us:
- v < 0, λ' < λ and f' > f
- which is a blue shift
e.g. a train whistle has a normal frequency of 550 Hz. If it is heard with a frequency of 580 Hz, is it moving towards or away from the observer?
- Towards
- Away
- It is stationary
e.g. a train whistle has a normal frequency of 550 Hz. If it is heard with a frequency of 580 Hz, what is the speed of the train?
- 3 ms-1
- 0.6 ms-1
- 17 ms-1
- 18 ms-1
Ultrasound
Very short wavelength sound can be used to image objects.
Pulses
- are produced by transducer (f ~ 6Mhz, c ~ 1500 ms-1. What would λ be)?
- travel through body
- are reflected by interfaces: e.g. weakly where one kind of tissue changes to another, strongly by bone
- reflected back to transducer
- turned into picture of body by measuring time delay. What would delay time for pulse reflected from backbone be?
|
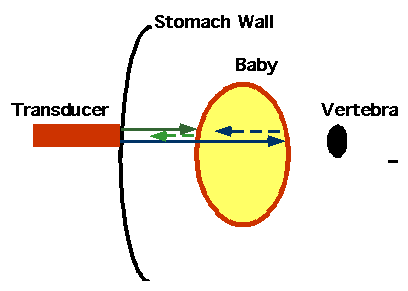 |
| Needs either transducer moved or (better) array of transducers to see full image. Non-invasive technique, with much less risk involved than with X-rays.
Can also use this with Doppler effect to see moving organs: e.g. to pick up foetal heart-beat.
Can step up power (to 107 W m-2) to zap kidney stones
Part of physics research at Carleton
http://www.physics.carleton.ca/~bog/index.html
|
 |
and now we talk about Temperature and Heat













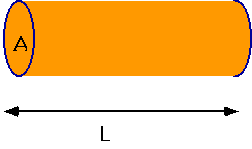

















 .
.

