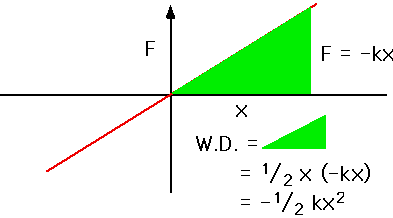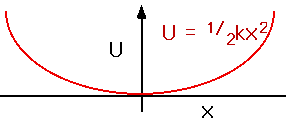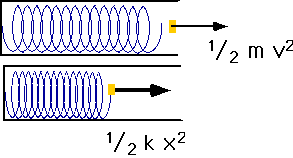BIT1002 Elasticity and SHM
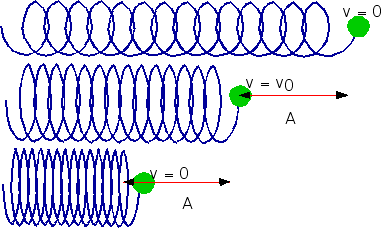
The Spring
One more special force:
- CEIIINSSSOTTUV
- which you will immediately realise is
- SIC VIS UT TENSIO
- which in turn you will translate as ...
- As the Force, thus the extension or as we say
- Hooke's Law
| extension ∝Force,
or
F = -kx
|
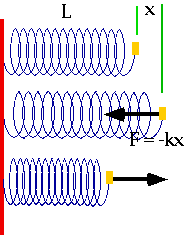 |
- Note
- Only the extension matters
- Force is in opposite direction to extension
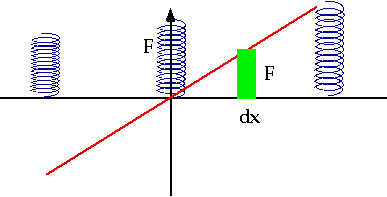
P.E. for spring:
Force varies, so we can't just use
W.D. = F x
but over short distance dx it is more-or- less constant
δW = F dx
which is the area of the green rect. |
 |
So the total W.D. is given by area under line. Hence the P.E. is .....
U = 1/2 k x2
|
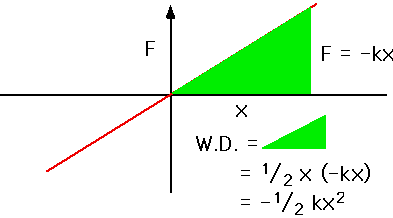 |
| Note that the P.E. is positive for x < 0 as well as x > 0: you can store energy in a stretched spring or a compressed spring. |
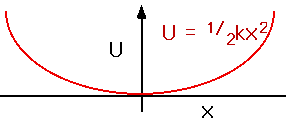 |
A toy gun consists of a spring which fires a 40 gm. cork. The spring can be compressed 1.5 cm by a 0.5 kg mass.
To fire the cork, the spring is pulled back 10 cm.
- What is k?
- What is the velocity when it is released
- How high will it go?
- If the spring is pulled back twice as far will its velocity
- Be twice as great
- Be four times as great
- Be 21/2 times as great?
- Be the same?
|
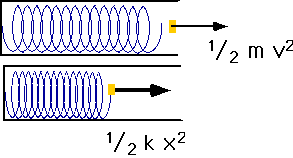 |
Elasticity
We have effectively assumed up to now that objects are not distorted by forces
| However, if a force is applied to a material, it will bend or break
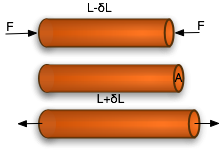
Simplest is Young's modulus: forces applied to each end of a bar will compress or stretch it |
 |
-
| Stress = Force/unit area |
= F/A
|
| Strain = extension/original extension |
= δL
L0
|
| Independent of whether we have an extension or compression,
(Stress) = E (Strain)
Hooke's law |
E = F L0
A δL
|
Young's modulus
E is Young's modulus or elastic modulus
As usual, reality is more complex
Stress-strain plot
- will remain linear up to some max (A),
- then be distorted (B),
- then represent some region where the material becomes permanently distorted (C)
- up to some "ultimate strength"(D) where it will break
|
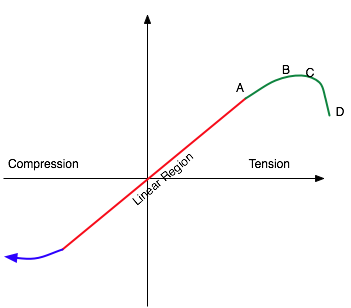 |
Compression and tension.
Young's moduli need not be the same
- Units: Stress is a form of pressure: Force/unit area = N m-2 = Pascals
-
(Pressure in meteorology: 1 atmosphere ~ 105 P = 100 kP) Strain is dimensionless, so
-
[E] = N m-2
- e.g how much would a 1.5 m long piano wire 0.3 mm in diameter stretch if you suspend a 5 kg weight from it? (E = 2x1011)
δL = F L0
E A
Ultimate strength
Breaking strain depends very much on whether material is stretched, compressed, sheared or twisted. Units also N m-2
| Material |
Tensile |
Compressive |
Shear |
| Steel |
5x108 |
5x108 |
2.5x108 |
| Concrete |
2x106 |
2x107 |
2x106 |
| Wood |
4x107 |
3.5x107 |
5x106 |
| Bone |
1.3x108 |
1.7x108 |
|
- e.g. bone has E = 1.6x1010, how much could Procrustes have stretched one's bones before they broke?
Simple Harmonic Motion
There are many forms of oscillatory motion is nature: e.g.
- Mass on Spring
- Pendulum
- Air track pendulum
- Stringless pendulum
- Ball in bowl
- Fortunately, all can be simplified to very similar mathematics
First some nomenclature
- Amplitude (A): size of swing
- Cycle: a complete oscillation (back and forward)
- Period (T): time for one cycle
- Note that there are two commonly used units for rotational/vibrational motion
- Frequency f = number of turns (vibrations)/s = 1/T usually called Hertz (Hz)
- Angular velocity ω (= no of radians/sec)
Relation is obvious: \color{red}{\omega = 2\pi f}
- Hertz also used for wave motion
Springs
Force from Hooke's Law
F = -kx
- x is extension (not the original length)
- - sign to get the direction right
- k is the spring constant
|
 |
- Then Newton's 2nd law can be used
F = ma = - kx
Warning
We are solving Newton's law
\color{red}{
ma = m\frac{{d^2 x}}{{dt^2 }} = - kx}
This is one place we have to use calculus: however we can cheat!
-
| There is a close mathematical relation between rotational and oscillatory motion: S.H.M. is "half" of rotational motion. |
|
- and the acceleration is
\color{red}{
a_x = \frac{{dv_x }}{{dt}} = - \frac{d}{{dt}}A\omega \sin \left( {\omega t} \right)}
-
or
\color{red}{
a = - A\omega ^2 \cos \left( {\omega t} \right)}
- but we want this to satisfy Newton's 2nd law
\color{red}{
ma = - kx}
-
so
\color{red}{
m\left( { - A\omega ^2 \cos \left( {\omega t} \right)} \right) = - k\left( {A\cos \left( {\omega t} \right)} \right)}
- which is O.K. provided
-
\color{red}{
\omega ^2 = \frac{k}{m}}
e.g. we have a spring with k = 1600N/m and a mass of 4 kg. The angular frequency ω is
- 20 rads/s
- 400 rads/s
- .0025 rads/s
e.g. we have a spring with k = 1600N/m and a mass of 4 kg so the angular frequency ω is 20 rads/sec. Hence the period is
- 3.18 s
- 126 s
- .314 s
- .008 s
e.g. What happens if we replace a mass by a heavier one? If you quadruple the mass on a spring, the period will change by a factor of
- 1
- 1/2
- 1/4
- 2
- 4
| Note that (apparently) any value of the amplitude is acceptable . In practice, this is only true for small oscillations: as long as the force law really is
F = -kx
|
|
Energy and S.H.M.
Physical Pendulum
Look at the Foucault pendulum in the entrance to Herzberg building:
Watch the animation.
In this case, tension in string supplies force to return bob to centre
a = -g x
L
with the same solution as before
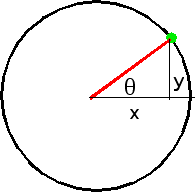
x = A sin(ωt)
or (better)
θ = θ0 cos(ωt)
|
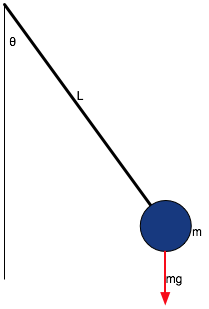 |
for a simple pendulum
Why do you walk with your arms extended, but jog with them bent?
- The natural rythmn of walking corresponds to your arms acting as pendulum.
- It helps to have your hands below waist-level
- It is a evolutionary leftover from when we walked with our hands touching the ground.
- It is psychologically more natural
What should the natural walking pace for an adult be (in steps/s)
- .1
- .5
- 1
- 2
- 5
Would a pendulum clock run fast or slow on the moon?
- fast because gravity is stronger
- fast because gravity is weaker
- slow because gravity is stronger
- slow because gravity is weaker
- The same time because time on the moon is the same as here
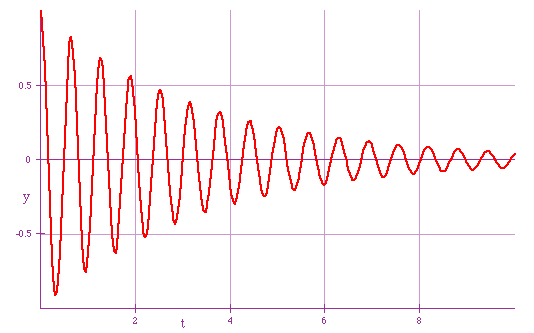
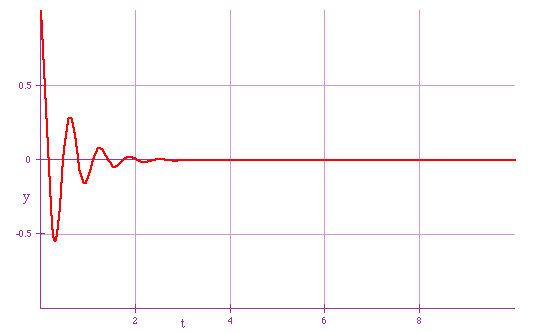
Damped S.H.M.
Reality rearing its ugly head again. If there is friction in the system, oscillations will die away
Formally, if the damping force
F ∝ v, then the solution would look like
y = y0e-atsin(ωt)
The frequency is almost the same, but the amplitude decreases exponentially with time
The extreme cases are
| a pendulum swinging in vacuum: almost undamped (a = 0.1 small) |
 |
| a pendulum swinging in syrup: will not complete one swing (a = 1.0 large) |
 |
- Up to now, we have assumed that the system is started off at some time and allowed to oscillate. However, can arrange for the system to be driven, so that driving force varies in time. Watch the demo:
- If driving frequency
ω0 matches natural frequency of system
ω, then size of oscillations grows
- k = 400 m = 10 so ω0 =(k/m)1/2 = .....?
- If driving frequency
ω matches natural frequency of system
ω0, then size of oscillations grows
- Usually some damping, so does not grow without limit
- Soldiers marching across bridge (did it ever happen?)
- Status: RO
From: "MIDN Zamberlan" <m017107@usna.edu> To: <watson@physics.carleton.ca>
Subject: Answering a rhetorical question
Date: Fri, 17 Nov 2000 01:28:03 -0500
X-Priority: 3
- I was reading your class on simple harmonic motion and you said "soldiers marching across bridge ,did it ever happen?" Well, actually I have seen it occur at the US Naval Academy. In '97 the freshmen, plebes, were out exercising and ran across a wooden footbridge in cadence. There was 50 of them. The bridge is about 200 ft long and once they reached the middle, two of the supports snapped and the bridge began to oscillate noticeably. The bridge was then condemned till a Naval Construction Battalion was able to repair it. I hope this answers your question.
Very respectfully,
RJ Zamberlan
MIDN, USN
- Bay of Fundy,
- hot air over beer bottles,
- wash-board roads,
- resonances in nuclei,
- electrons in an AC circuit and...............................
-
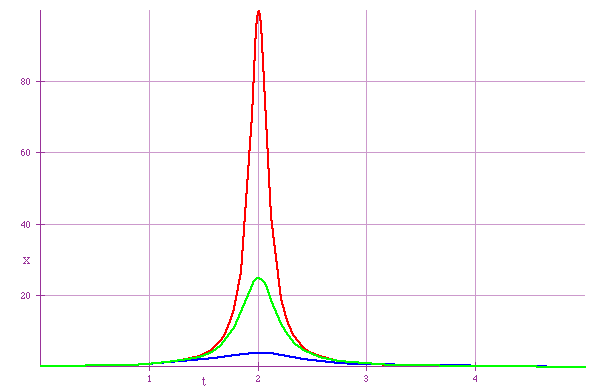
Previously we have regarded the amplitude as being an uninteresting constant. If the system is driven, then the response depends on how near resonance we are. The actual formula for the response is
A = A0
(w-w0)2+ γ2
| What does this look like?
For γ= .1, .2, .5 |
 |
-
| It is easier to see this if we make them all have the same height |
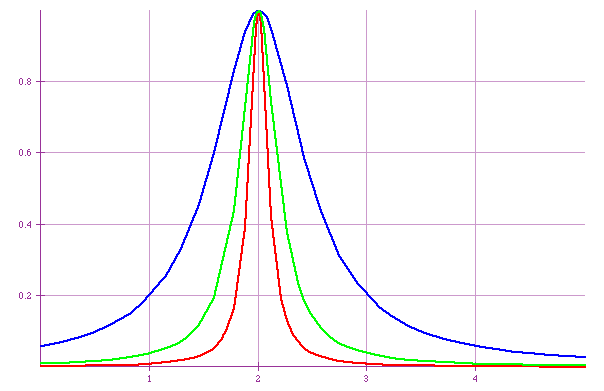 |
-
Now we go to waves and sound