

A novel imaging method using flat panel detector
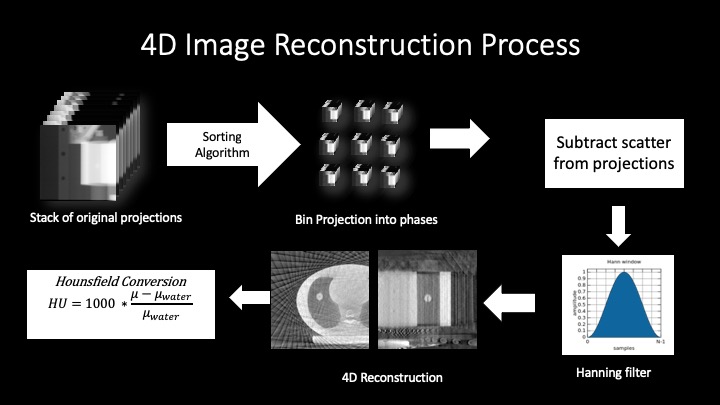
Four-dimensional, cone-beam CT (4D CBCT) substantially reduces motion blurring artifacts introduced by thorax motion caused by the respiration in three-dimension CBCT (3D CBCT). However 4D CBCT degrades considerably the image quality compared to a 3D CBCT. In this study we investigate the image acquisition parameters, namely, collimation (small vs medium Field of View (FOV)), and filtration. We conclude that the best image quality, within a reasonable acquisition time and number of projections, was with the medium FOV “Fast” acquisition (~1218 Projections, ~3.7 minutes). In this time frame it provides a reasonably good image for the purposes of patient positioning. To allow for off-line reconstruction and analysis of these images, we built a 4D CBCT reconstruction process using RTK and compared it to the clinical XVI system it.
Lung caner imaging
Lung tumors' positions are time varient, meaning that they move. Making it challengin to radiate.
Computing and developing software
Each scan can be many gigabytes of infomation and thousants of files. To handle, manage, and process this data custom software was developed.
Scan 4D reconsturction
The reconstruction sfotware was depolyed on an disbrtutaed computing cluster for faster processing.
Feldkamp-Davis-Kress method
Feldkamp-Davis-Kress method (FDK) is an extension of the Filtered back-projection method to cone-beam geometry also known as the Radon Transform used in the conventional Fan Beam CT. Here we first show the workings of the Radon transform for 2D in the form of a convolution and then projection. When imaging an object made up of different materials, each of which have different attenuation coefficient ($\mu$), x-rays ($I$) are sent from a source parallel to a detector, such that the x-ray passes through the object and lands on the detector ( the resulting beam intensity is $I_0$). Each x-ray beam attenuates a certain amount depending on how much energy was aborted by the object. As shown in figure $$I=I_0exp(-\int_{path} \mu(x)dx) => \int_{path}\mu(x)dx = -ln(\frac{I}{I_0}) $$ The Radon transform of an image represented by the function $\mu(x,y)$ can be defined as a series of line integrals through $\mu(x,y)$ at different offsets from the origin. Which is mathematically defined as follows: $$R(r,\theta)=\iint_{-\infty}^{\infty} \mu(x,y) \delta(x cos\theta + y sin\theta-r) dx dy $$ Where $\theta$ is the angle of the line, and r is the perpendicular offset of the line. The resulting Radon transform is called a sinogram. In order to reconstruct the image from the sinogram, the inverse Radon transform is to sinogram. There are several methods to compute the inverse Radon transform but the one of interest in this study is the Filtered Back Projection method. This method is split into two phases, the projection and the filtration on the image. The projection phase is very similar to the Radon transform described above, except now the path integral are projected back onto a plane at their respective angles. This back-projection phase takes the form: $$f(x,y)=\int^\pi_0 R(x cos(\theta + y sin\theta, \theta)$$
Although the shape of the object is reconstructed, the reconstructed image is very noisy. To correct for this noise a high pass and Hanning filter is applied to the sinogram data in the frequency domain. Applying these filters significantly improves the quality of the reconstructed image. The FDK Methods extends the Radon transform to conical projections, and the transform can be given by the following: $$f_{FDK}(x,y,z)=\int^{2\pi}_0 \frac{R^2}{U(x,y,\beta)^2} \mu^F (\beta,a(x,y,\beta),b(x,y,z,\beta))\delta\beta$$ The detector position is given by: $$a(x,y,\beta)=R \frac{-x sin \beta +y cos \beta}{r + x cos \beta + y sin \beta}$$ $b(x,y,z,\beta)$ is given by: $$b(x,y,z,\beta)=z \frac{\beta}{R + x cos \beta + y sin \ beta}$$ The function $U(x,y,\beta)$ is the function of the distance between the source and the line parallel with the detector and is given by: $$U(x,y,\beta)=R+x cos\beta+y sin\beta$$
Real Results
Acquired the first very 4D CBCT images at the Ottawa Hospital Cancer Center.
Built 4DCBCT reconstruction process using RTK and compared to the clinical XVI system
Concluded that the best image quality was with the medium FOV “Fast” acquisition (1218 Projections)
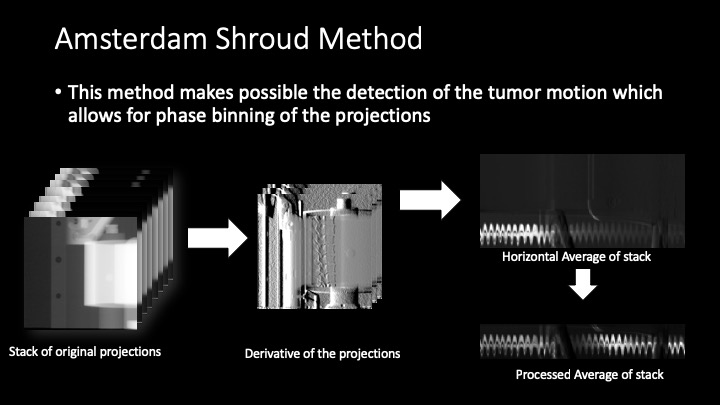
Concluded the position of the tumor after sorting/binning is in the expected position (95% confidence bounds)